EB-MBD: Emerging-Barrier Model-Based Diffusion for Safe Trajectory Optimization in Highly Constrained Environments

We propose enforcing constraints on Model-Based Diffusion by introducing emerging barrier functions inspired by interior point methods. We show that constraints on Model-Based Diffusion can lead to catastrophic performance degradation, even on simple 2D systems due to sample inefficiency in the Monte Carlo approximation of the score function. We introduce Emerging-Barrier Model-Based Diffusion (EB-MBD) which uses progressively introduced barrier constraints to avoid these problems, significantly improving solution quality, without the need for computationally expensive operations such as projections. We analyze the sampling liveliness of samples each iteration to inform barrier parameter scheduling choice. We demonstrate results for 2D collision avoidance and a 3D underwater manipulator system and show that our method achieves lower cost solutions than Model-Based Diffusion, and requires orders of magnitude less computation time than projection based methods.

Learning to optimize with guarantees: a complete characterization of linearly convergent algorithms

In high-stakes engineering applications, optimization algorithms must come with provable worst-case guarantees over a mathematically defined class of problems. Designing for the worst case, however, inevitably sacrifices performance on the specific problem instances that often occur in practice. We address the problem of augmenting a given linearly convergent algorithm to improve its average-case performance on a restricted set of target problems - for example, tailoring an off-the-shelf solver for model predictive control (MPC) for an application to a specific dynamical system - while preserving its worst-case guarantees across the entire problem class. Toward this goal, we characterize the class of algorithms that achieve linear convergence for classes of nonsmooth composite optimization problems. In particular, starting from a baseline linearly convergent algorithm, we derive all - and only - the modifications to its update rule that maintain its convergence properties. Our results apply to augmenting legacy algorithms such as gradient descent for nonconvex, gradient-dominated functions; Nesterov's accelerated method for strongly convex functions; and projected methods for optimization over polyhedral feasibility sets. We showcase effectiveness of the approach on solving optimization problems with tight iteration budgets in application to ill-conditioned systems of linear equations and MPC for linear systems.

Robustly Invertible Nonlinear Dynamics and the BiLipREN: Contracting Neural Models with Contracting Inverses

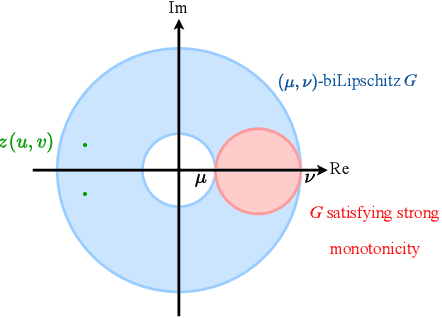
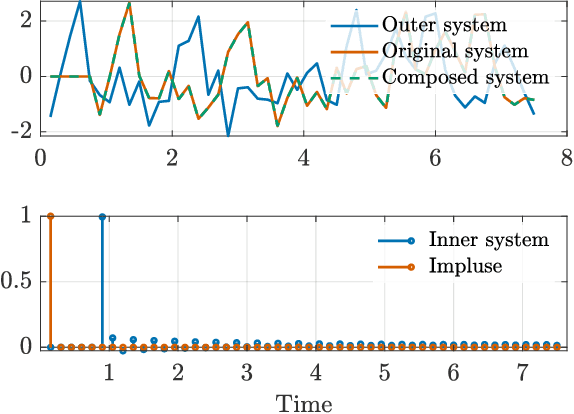
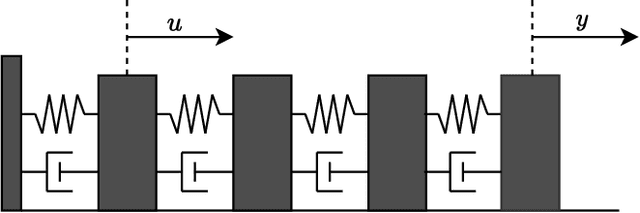
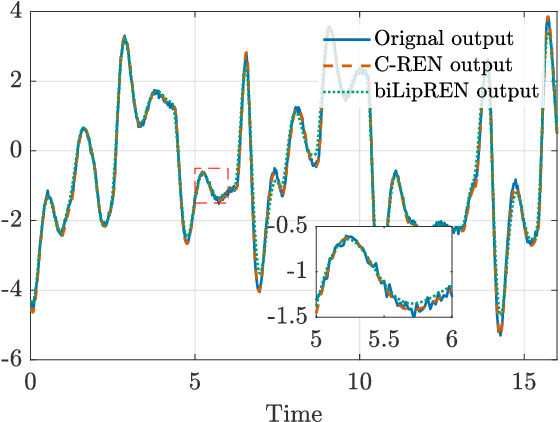
We study the invertibility of nonlinear dynamical systems from the perspective of contraction and incremental stability analysis and propose a new invertible recurrent neural model: the BiLipREN. In particular, we consider a nonlinear state space model to be robustly invertible if an inverse exists with a state space realisation, and both the forward model and its inverse are contracting, i.e. incrementally exponentially stable, and Lipschitz, i.e. have bounded incremental gain. This property of bi-Lipschitzness implies both robustness in the sense of sensitivity to input perturbations, as well as robust distinguishability of different inputs from their corresponding outputs, i.e. the inverse model robustly reconstructs the input sequence despite small perturbations to the initial conditions and measured output. Building on this foundation, we propose a parameterization of neural dynamic models: bi-Lipschitz recurrent equilibrium networks (biLipREN), which are robustly invertible by construction. Moreover, biLipRENs can be composed with orthogonal linear systems to construct more general bi-Lipschitz dynamic models, e.g., a nonlinear analogue of minimum-phase/all-pass (inner/outer) factorization. We illustrate the utility of our proposed approach with numerical examples.

Negative Imaginary Neural ODEs: Learning to Control Mechanical Systems with Stability Guarantees

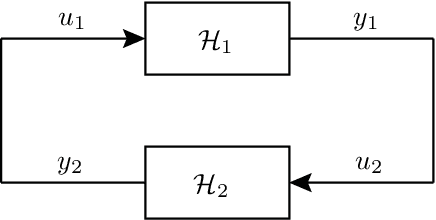
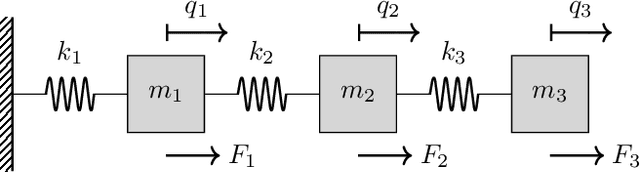
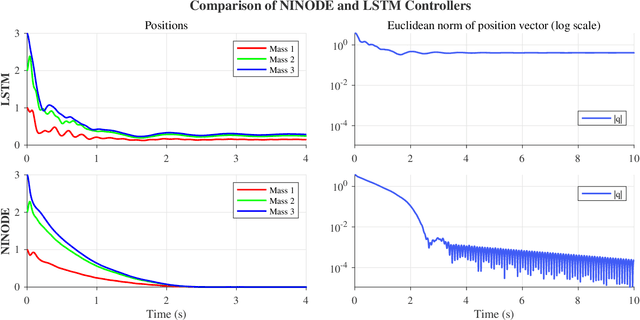
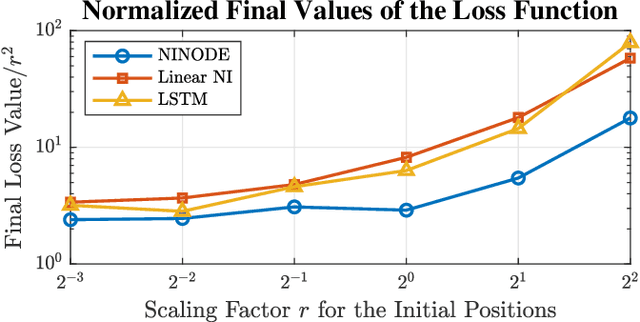
We propose a neural control method to provide guaranteed stabilization for mechanical systems using a novel negative imaginary neural ordinary differential equation (NINODE) controller. Specifically, we employ neural networks with desired properties as state-space function matrices within a Hamiltonian framework to ensure the system possesses the NI property. This NINODE system can serve as a controller that asymptotically stabilizes an NI plant under certain conditions. For mechanical plants with colocated force actuators and position sensors, we demonstrate that all the conditions required for stability can be translated into regularity constraints on the neural networks used in the controller. We illustrate the utility, effectiveness, and stability guarantees of the NINODE controller through an example involving a nonlinear mass-spring system.

R2DN: Scalable Parameterization of Contracting and Lipschitz Recurrent Deep Networks

This paper presents the Robust Recurrent Deep Network (R2DN), a scalable parameterization of robust recurrent neural networks for machine learning and data-driven control. We construct R2DNs as a feedback interconnection of a linear time-invariant system and a 1-Lipschitz deep feedforward network, and directly parameterize the weights so that our models are stable (contracting) and robust to small input perturbations (Lipschitz) by design. Our parameterization uses a structure similar to the previously-proposed recurrent equilibrium networks (RENs), but without the requirement to iteratively solve an equilibrium layer at each time-step. This speeds up model evaluation and backpropagation on GPUs, and makes it computationally feasible to scale up the network size, batch size, and input sequence length in comparison to RENs. We compare R2DNs to RENs on three representative problems in nonlinear system identification, observer design, and learning-based feedback control and find that training and inference are both up to an order of magnitude faster with similar test set performance, and that training/inference times scale more favorably with respect to model expressivity.

Training Trajectory Predictors Without Ground-Truth Data

This paper presents a framework capable of accurately and smoothly estimating position, heading, and velocity. Using this high-quality input, we propose a system based on Trajectron++, able to consistently generate precise trajectory predictions. Unlike conventional models that require ground-truth data for training, our approach eliminates this dependency. Our analysis demonstrates that poor quality input leads to noisy and unreliable predictions, which can be detrimental to navigation modules. We evaluate both input data quality and model output to illustrate the impact of input noise. Furthermore, we show that our estimation system enables effective training of trajectory prediction models even with limited data, producing robust predictions across different environments. Accurate estimations are crucial for deploying trajectory prediction models in real-world scenarios, and our system ensures meaningful and reliable results across various application contexts.

Norm-Bounded Low-Rank Adaptation

In this work, we propose norm-bounded low-rank adaptation (NB-LoRA) for parameter-efficient fine tuning. We introduce two parameterizations that allow explicit bounds on each singular value of the weight adaptation matrix, which can therefore satisfy any prescribed unitarily invariant norm bound, including the Schatten norms (e.g., nuclear, Frobenius, spectral norm). The proposed parameterizations are unconstrained and complete, i.e. they cover all matrices satisfying the prescribed rank and norm constraints. Experiments on vision fine-tuning benchmarks show that the proposed approach can achieve good adaptation performance while avoiding model catastrophic forgetting and also substantially improve robustness to a wide range of hyper-parameters, including adaptation rank, learning rate and number of training epochs. We also explore applications in privacy-preserving model merging and low-rank matrix completion.

Real-time Coupled Centroidal Motion and Footstep Planning for Biped Robots

This paper presents an algorithm that finds a centroidal motion and footstep plan for a Spring-Loaded Inverted Pendulum (SLIP)-like bipedal robot model substantially faster than real-time. This is achieved with a novel representation of the dynamic footstep planning problem, where each point in the environment is considered a potential foothold that can apply a force to the center of mass to keep it on a desired trajectory. For a biped, up to two such footholds per time step must be selected, and we approximate this cardinality constraint with an iteratively reweighted $l_1$-norm minimization. Along with a linearizing approximation of an angular momentum constraint, this results in a quadratic program can be solved for a contact schedule and center of mass trajectory with automatic gait discovery. A 2 s planning horizon with 13 time steps and 20 surfaces available at each time is solved in 142 ms, roughly ten times faster than comparable existing methods in the literature. We demonstrate the versatility of this program in a variety of simulated environments.

Path-Parameterised RRTs for Underactuated Systems

We present a sample-based motion planning algorithm specialised to a class of underactuated systems using path parameterisation. The structure this class presents under a path parameterisation enables the trivial computation of dynamic feasibility along a path. Using this, a specialised state-based steering mechanism within an RRT motion planning algorithm is developed, enabling the generation of both geometric paths and their time parameterisations without introducing excessive computational overhead. We find with two systems that our algorithm computes feasible trajectories with higher rates of success and lower mean computation times compared to existing approaches.

On Robust Reinforcement Learning with Lipschitz-Bounded Policy Networks

This paper presents a study of robust policy networks in deep reinforcement learning. We investigate the benefits of policy parameterizations that naturally satisfy constraints on their Lipschitz bound, analyzing their empirical performance and robustness on two representative problems: pendulum swing-up and Atari Pong. We illustrate that policy networks with small Lipschitz bounds are significantly more robust to disturbances, random noise, and targeted adversarial attacks than unconstrained policies composed of vanilla multi-layer perceptrons or convolutional neural networks. Moreover, we find that choosing a policy parameterization with a non-conservative Lipschitz bound and an expressive, nonlinear layer architecture gives the user much finer control over the performance-robustness trade-off than existing state-of-the-art methods based on spectral normalization.