dLITE: Differentiable Lighting-Informed Trajectory Evaluation for On-Orbit Inspection

Visual inspection of space-borne assets is of increasing interest to spacecraft operators looking to plan maintenance, characterise damage, and extend the life of high-value satellites in orbit. The environment of Low Earth Orbit (LEO) presents unique challenges when planning inspection operations that maximise visibility, information, and data quality. Specular reflection of sunlight from spacecraft bodies, self-shadowing, and dynamic lighting in LEO significantly impact the quality of data captured throughout an orbit. This is exacerbated by the relative motion between spacecraft, which introduces variable imaging distances and attitudes during inspection. Planning inspection trajectories with the aide of simulation is a common approach. However, the ability to design and optimise an inspection trajectory specifically to improve the resulting image quality in proximity operations remains largely unexplored. In this work, we present $\partial$LITE, an end-to-end differentiable simulation pipeline for on-orbit inspection operations. We leverage state-of-the-art differentiable rendering tools and a custom orbit propagator to enable end-to-end optimisation of orbital parameters based on visual sensor data. $\partial$LITE enables us to automatically design non-obvious trajectories, vastly improving the quality and usefulness of attained data. To our knowledge, our differentiable inspection-planning pipeline is the first of its kind and provides new insights into modern computational approaches to spacecraft mission planning. Project page: https://appearance-aware.github.io/dlite/

R2DN: Scalable Parameterization of Contracting and Lipschitz Recurrent Deep Networks

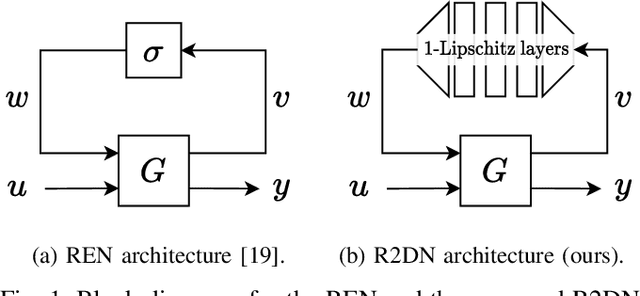
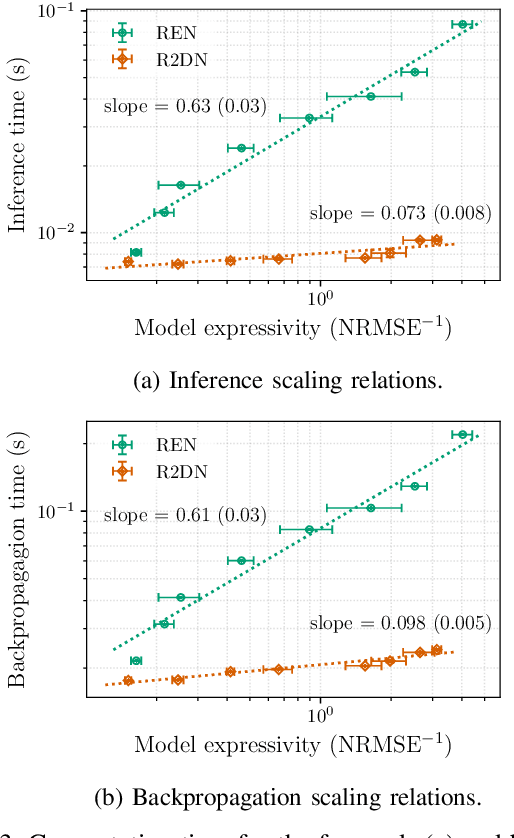
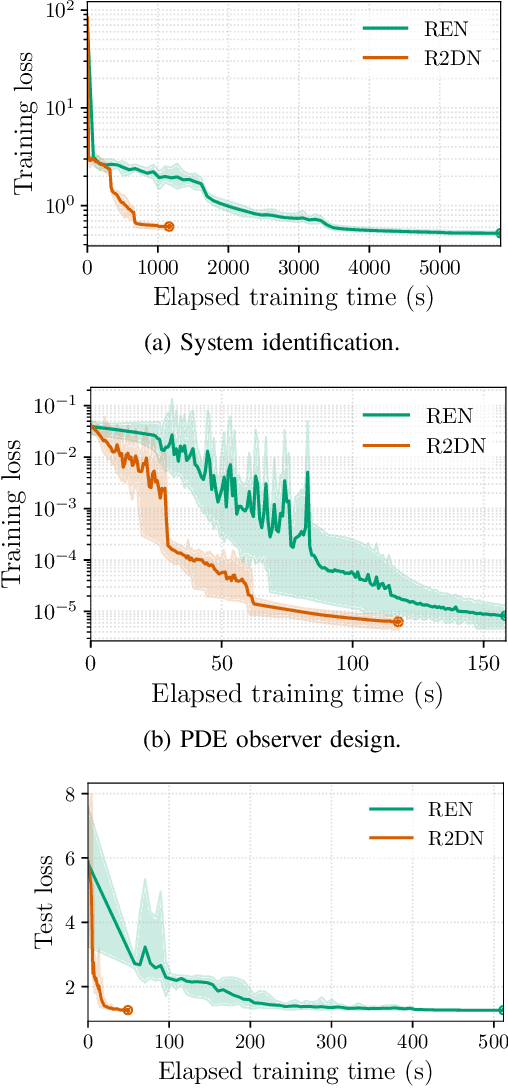
This paper presents the Robust Recurrent Deep Network (R2DN), a scalable parameterization of robust recurrent neural networks for machine learning and data-driven control. We construct R2DNs as a feedback interconnection of a linear time-invariant system and a 1-Lipschitz deep feedforward network, and directly parameterize the weights so that our models are stable (contracting) and robust to small input perturbations (Lipschitz) by design. Our parameterization uses a structure similar to the previously-proposed recurrent equilibrium networks (RENs), but without the requirement to iteratively solve an equilibrium layer at each time-step. This speeds up model evaluation and backpropagation on GPUs, and makes it computationally feasible to scale up the network size, batch size, and input sequence length in comparison to RENs. We compare R2DNs to RENs on three representative problems in nonlinear system identification, observer design, and learning-based feedback control and find that training and inference are both up to an order of magnitude faster with similar test set performance, and that training/inference times scale more favorably with respect to model expressivity.

On Robust Reinforcement Learning with Lipschitz-Bounded Policy Networks

This paper presents a study of robust policy networks in deep reinforcement learning. We investigate the benefits of policy parameterizations that naturally satisfy constraints on their Lipschitz bound, analyzing their empirical performance and robustness on two representative problems: pendulum swing-up and Atari Pong. We illustrate that policy networks with small Lipschitz bounds are significantly more robust to disturbances, random noise, and targeted adversarial attacks than unconstrained policies composed of vanilla multi-layer perceptrons or convolutional neural networks. Moreover, we find that choosing a policy parameterization with a non-conservative Lipschitz bound and an expressive, nonlinear layer architecture gives the user much finer control over the performance-robustness trade-off than existing state-of-the-art methods based on spectral normalization.

RobustNeuralNetworks.jl: a Package for Machine Learning and Data-Driven Control with Certified Robustness

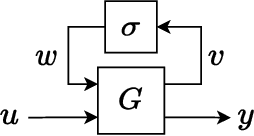
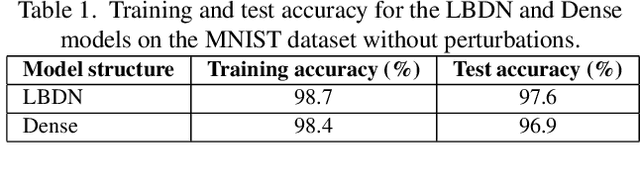
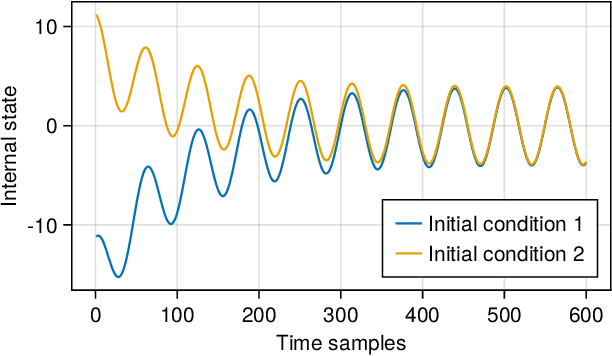
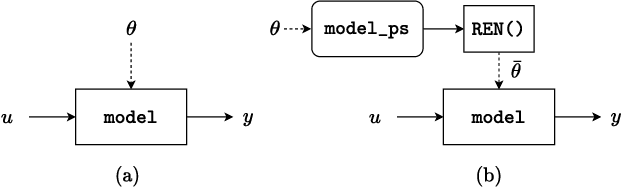
Neural networks are typically sensitive to small input perturbations, leading to unexpected or brittle behaviour. We present RobustNeuralNetworks.jl: a Julia package for neural network models that are constructed to naturally satisfy a set of user-defined robustness constraints. The package is based on the recently proposed Recurrent Equilibrium Network (REN) and Lipschitz-Bounded Deep Network (LBDN) model classes, and is designed to interface directly with Julia's most widely-used machine learning package, Flux.jl. We discuss the theory behind our model parameterization, give an overview of the package, and provide a tutorial demonstrating its use in image classification, reinforcement learning, and nonlinear state-observer design.

Learning Over All Contracting and Lipschitz Closed-Loops for Partially-Observed Nonlinear Systems

This paper presents a policy parameterization for learning-based control on nonlinear, partially-observed dynamical systems. The parameterization is based on a nonlinear version of the Youla parameterization and the recently proposed Recurrent Equilibrium Network (REN) class of models. We prove that the resulting Youla-REN parameterization automatically satisfies stability (contraction) and user-tunable robustness (Lipschitz) conditions on the closed-loop system. This means it can be used for safe learning-based control with no additional constraints or projections required to enforce stability or robustness. We test the new policy class in simulation on two reinforcement learning tasks: 1) magnetic suspension, and 2) inverting a rotary-arm pendulum. We find that the Youla-REN performs similarly to existing learning-based and optimal control methods while also ensuring stability and exhibiting improved robustness to adversarial disturbances.