RobustNeuralNetworks.jl: a Package for Machine Learning and Data-Driven Control with Certified Robustness

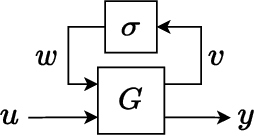
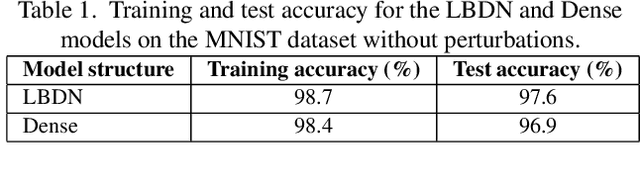
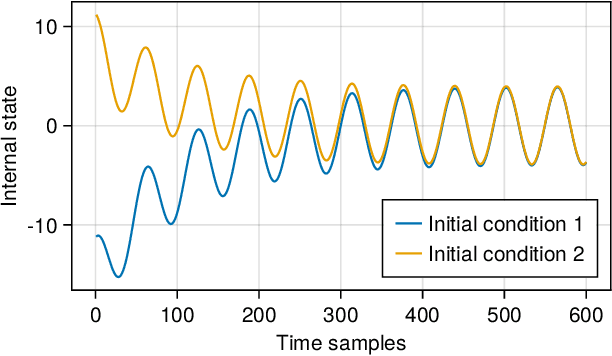
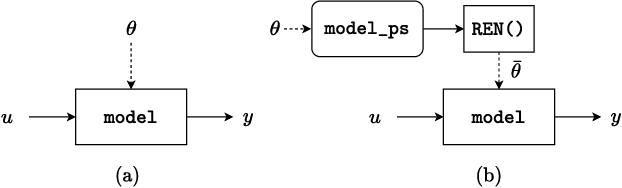
Neural networks are typically sensitive to small input perturbations, leading to unexpected or brittle behaviour. We present RobustNeuralNetworks.jl: a Julia package for neural network models that are constructed to naturally satisfy a set of user-defined robustness constraints. The package is based on the recently proposed Recurrent Equilibrium Network (REN) and Lipschitz-Bounded Deep Network (LBDN) model classes, and is designed to interface directly with Julia's most widely-used machine learning package, Flux.jl. We discuss the theory behind our model parameterization, give an overview of the package, and provide a tutorial demonstrating its use in image classification, reinforcement learning, and nonlinear state-observer design.

Learning over All Stabilizing Nonlinear Controllers for a Partially-Observed Linear System

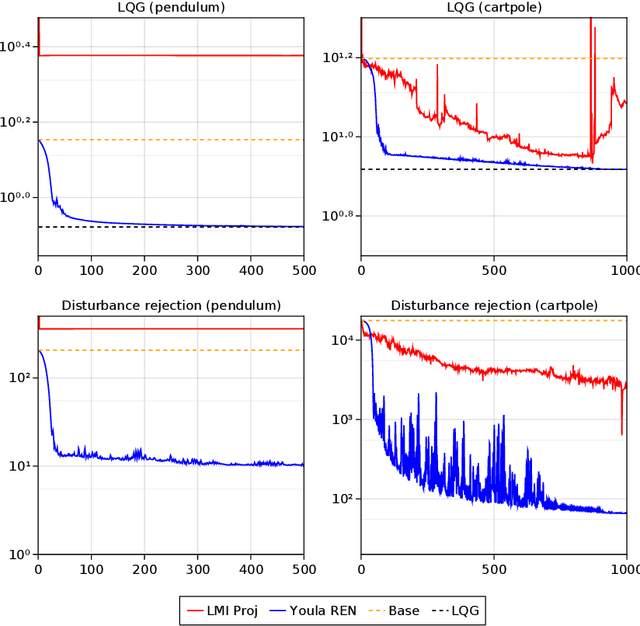
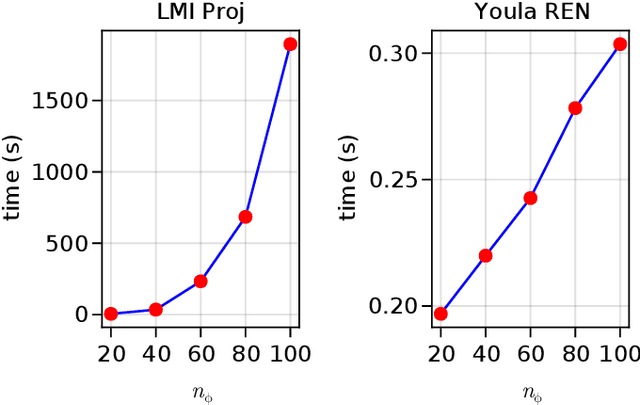
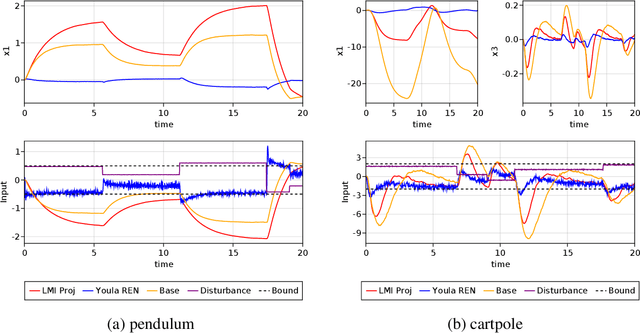
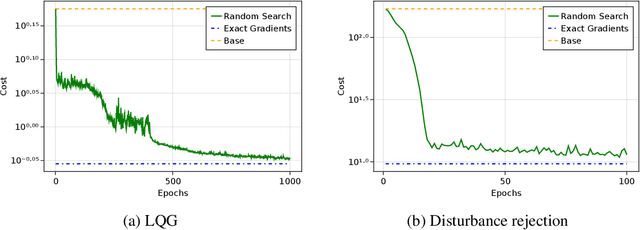
We propose a parameterization of nonlinear output feedback controllers for linear dynamical systems based on a recently developed class of neural network called the recurrent equilibrium network (REN), and a nonlinear version of the Youla parameterization. Our approach guarantees the closed-loop stability of partially observable linear dynamical systems without requiring any constraints to be satisfied. This significantly simplifies model fitting as any unconstrained optimization procedure can be applied whilst still maintaining stability. We demonstrate our method on reinforcement learning tasks with both exact and approximate gradient methods. Simulation studies show that our method is significantly more scalable and significantly outperforms other approaches in the same problem setting.

Distributed Identification of Contracting and/or Monotone Network Dynamics

This paper proposes methods for identification of large-scale networked systems with guarantees that the resulting model will be contracting -- a strong form of nonlinear stability -- and/or monotone, i.e. order relations between states are preserved. The main challenges that we address are: simultaneously searching for model parameters and a certificate of stability, and scalability to networks with hundreds or thousands of nodes. We propose a model set that admits convex constraints for stability and monotonicity, and has a separable structure that allows distributed identification via the alternating directions method of multipliers (ADMM). The performance and scalability of the approach is illustrated on a variety of linear and non-linear case studies, including a nonlinear traffic network with a 200-dimensional state space.

Recurrent Equilibrium Networks: Unconstrained Learning of Stable and Robust Dynamical Models

This paper introduces recurrent equilibrium networks (RENs), a new class of nonlinear dynamical models for applications in machine learning and system identification. The new model class has "built in" guarantees of stability and robustness: all models in the class are contracting -- a strong form of nonlinear stability -- and models can have prescribed Lipschitz bounds. RENs are otherwise very flexible: they can represent all stable linear systems, all previously-known sets of contracting recurrent neural networks, all deep feedforward neural networks, and all stable Wiener/Hammerstein models. RENs are parameterized directly by a vector in R^N, i.e. stability and robustness are ensured without parameter constraints, which simplifies learning since generic methods for unconstrained optimization can be used. The performance of the robustness of the new model set is evaluated on benchmark nonlinear system identification problems.

Lipschitz Bounded Equilibrium Networks

This paper introduces new parameterizations of equilibrium neural networks, i.e. networks defined by implicit equations. This model class includes standard multilayer and residual networks as special cases. The new parameterization admits a Lipschitz bound during training via unconstrained optimization: no projections or barrier functions are required. Lipschitz bounds are a common proxy for robustness and appear in many generalization bounds. Furthermore, compared to previous works we show well-posedness (existence of solutions) under less restrictive conditions on the network weights and more natural assumptions on the activation functions: that they are monotone and slope restricted. These results are proved by establishing novel connections with convex optimization, operator splitting on non-Euclidean spaces, and contracting neural ODEs. In image classification experiments we show that the Lipschitz bounds are very accurate and improve robustness to adversarial attacks.

Convex Sets of Robust Recurrent Neural Networks

Recurrent neural networks (RNNs) are a class of nonlinear dynamical systems often used to model sequence-to-sequence maps. RNNs have been shown to have excellent expressive power but lack stability or robustness guarantees that would be necessary for safety-critical applications. In this paper we formulate convex sets of RNNs with guaranteed stability and robustness properties. The guarantees are derived using differential IQC methods and can ensure contraction (global exponential stability of all solutions) and bounds on incremental l2 gain (the Lipschitz constant of the learnt sequence-to-sequence mapping). An implicit model structure is employed to construct a jointly-convex representation of an RNN and its certificate of stability or robustness. We prove that the proposed model structure includes all previously-proposed convex sets of contracting RNNs as special cases, and also includes all stable linear dynamical systems. We demonstrate the utility of the proposed model class in the context of nonlinear system identification.

Contracting Implicit Recurrent Neural Networks: Stable Models with Improved Trainability

Stability of recurrent models is closely linked with trainability, generalizability and in some applications, safety. Methods that train stable recurrent neural networks, however, do so at a significant cost to expressibility. We propose an implicit model structure that allows for a convex parametrization of stable models using contraction analysis of non-linear systems. Using these stability conditions we propose a new approach to model initialization and then provide a number of empirical results comparing the performance of our proposed model set to previous stable RNNs and vanilla RNNs. By carefully controlling stability in the model, we observe a significant increase in the speed of training and model performance.