Learning over All Stabilizing Nonlinear Controllers for a Partially-Observed Linear System

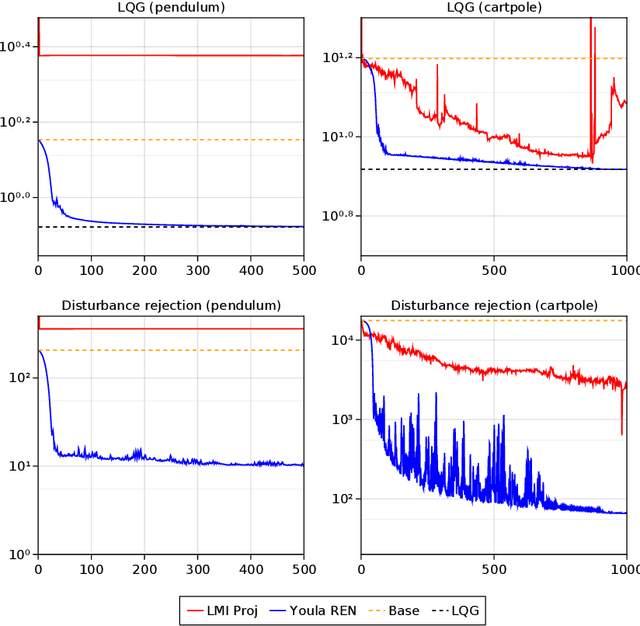
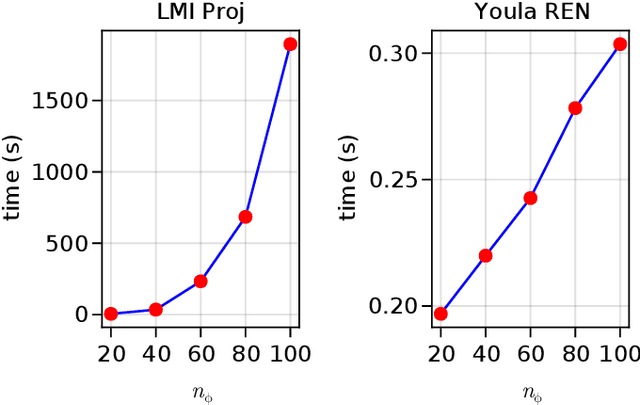
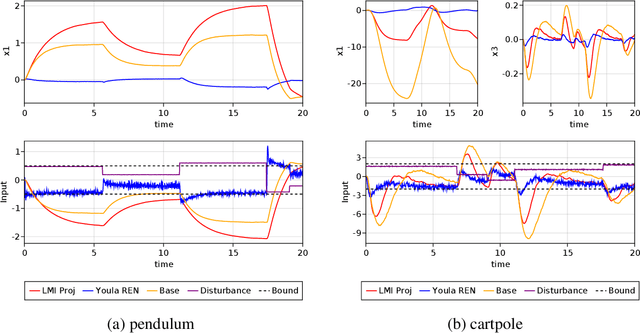
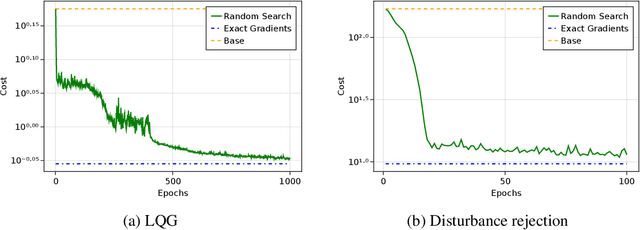
We propose a parameterization of nonlinear output feedback controllers for linear dynamical systems based on a recently developed class of neural network called the recurrent equilibrium network (REN), and a nonlinear version of the Youla parameterization. Our approach guarantees the closed-loop stability of partially observable linear dynamical systems without requiring any constraints to be satisfied. This significantly simplifies model fitting as any unconstrained optimization procedure can be applied whilst still maintaining stability. We demonstrate our method on reinforcement learning tasks with both exact and approximate gradient methods. Simulation studies show that our method is significantly more scalable and significantly outperforms other approaches in the same problem setting.