Multi-Agent Bayesian Optimization with Coupled Black-Box and Affine Constraints
Paper and Code
Oct 02, 2023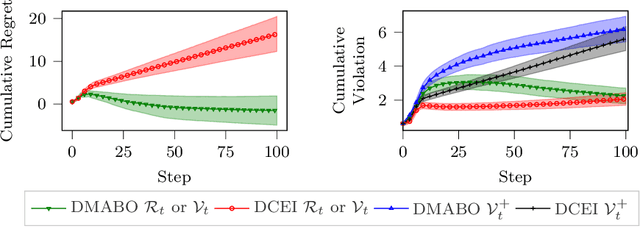
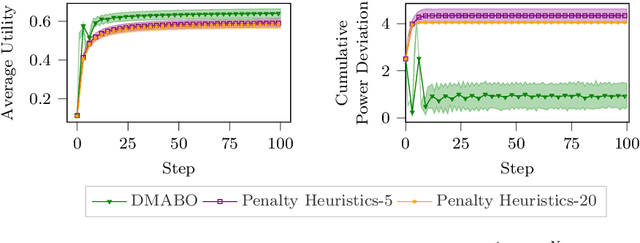
This paper studies the problem of distributed multi-agent Bayesian optimization with both coupled black-box constraints and known affine constraints. A primal-dual distributed algorithm is proposed that achieves similar regret/violation bounds as those in the single-agent case for the black-box objective and constraint functions. Additionally, the algorithm guarantees an $\mathcal{O}(N\sqrt{T})$ bound on the cumulative violation for the known affine constraints, where $N$ is the number of agents. Hence, it is ensured that the average of the samples satisfies the affine constraints up to the error $\mathcal{O}({N}/{\sqrt{T}})$. Furthermore, we characterize certain conditions under which our algorithm can bound a stronger metric of cumulative violation and provide best-iterate convergence without affine constraint. The method is then applied to both sampled instances from Gaussian processes and a real-world optimal power allocation problem for wireless communication; the results show that our method simultaneously provides close-to-optimal performance and maintains minor violations on average, corroborating our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge