Bayesian Optimisation with Unknown Hyperparameters: Regret Bounds Logarithmically Closer to Optimal
Paper and Code
Oct 14, 2024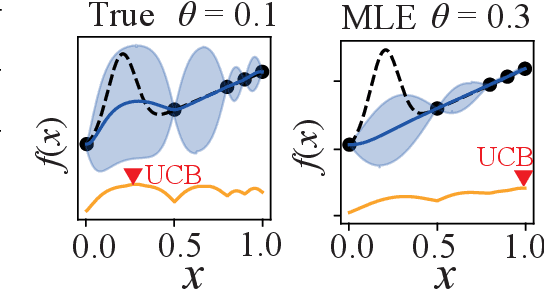

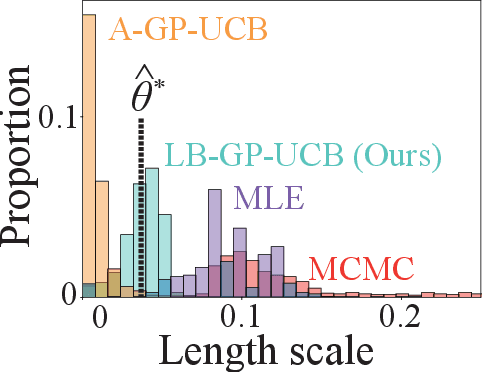
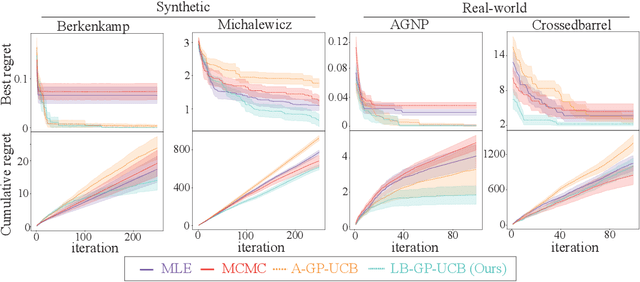
Bayesian Optimization (BO) is widely used for optimising black-box functions but requires us to specify the length scale hyperparameter, which defines the smoothness of the functions the optimizer will consider. Most current BO algorithms choose this hyperparameter by maximizing the marginal likelihood of the observed data, albeit risking misspecification if the objective function is less smooth in regions we have not yet explored. The only prior solution addressing this problem with theoretical guarantees was A-GP-UCB, proposed by Berkenkamp et al. (2019). This algorithm progressively decreases the length scale, expanding the class of functions considered by the optimizer. However, A-GP-UCB lacks a stopping mechanism, leading to over-exploration and slow convergence. To overcome this, we introduce Length scale Balancing (LB) - a novel approach, aggregating multiple base surrogate models with varying length scales. LB intermittently adds smaller length scale candidate values while retaining longer scales, balancing exploration and exploitation. We formally derive a cumulative regret bound of LB and compare it with the regret of an oracle BO algorithm using the optimal length scale. Denoting the factor by which the regret bound of A-GP-UCB was away from oracle as $g(T)$, we show that LB is only $\log g(T)$ away from oracle regret. We also empirically evaluate our algorithm on synthetic and real-world benchmarks and show it outperforms A-GP-UCB, maximum likelihood estimation and MCMC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge