A Quadrature Approach for General-Purpose Batch Bayesian Optimization via Probabilistic Lifting

Parallelisation in Bayesian optimisation is a common strategy but faces several challenges: the need for flexibility in acquisition functions and kernel choices, flexibility dealing with discrete and continuous variables simultaneously, model misspecification, and lastly fast massive parallelisation. To address these challenges, we introduce a versatile and modular framework for batch Bayesian optimisation via probabilistic lifting with kernel quadrature, called SOBER, which we present as a Python library based on GPyTorch/BoTorch. Our framework offers the following unique benefits: (1) Versatility in downstream tasks under a unified approach. (2) A gradient-free sampler, which does not require the gradient of acquisition functions, offering domain-agnostic sampling (e.g., discrete and mixed variables, non-Euclidean space). (3) Flexibility in domain prior distribution. (4) Adaptive batch size (autonomous determination of the optimal batch size). (5) Robustness against a misspecified reproducing kernel Hilbert space. (6) Natural stopping criterion.

Domain-Agnostic Batch Bayesian Optimization with Diverse Constraints via Bayesian Quadrature

Real-world optimisation problems often feature complex combinations of (1) diverse constraints, (2) discrete and mixed spaces, and are (3) highly parallelisable. (4) There are also cases where the objective function cannot be queried if unknown constraints are not satisfied, e.g. in drug discovery, safety on animal experiments (unknown constraints) must be established before human clinical trials (querying objective function) may proceed. However, most existing works target each of the above three problems in isolation and do not consider (4) unknown constraints with query rejection. For problems with diverse constraints and/or unconventional input spaces, it is difficult to apply these techniques as they are often mutually incompatible. We propose cSOBER, a domain-agnostic prudent parallel active sampler for Bayesian optimisation, based on SOBER of Adachi et al. (2023). We consider infeasibility under unknown constraints as a type of integration error that we can estimate. We propose a theoretically-driven approach that propagates such error as a tolerance in the quadrature precision that automatically balances exploitation and exploration with the expected rejection rate. Moreover, our method flexibly accommodates diverse constraints and/or discrete and mixed spaces via adaptive tolerance, including conventional zero-risk cases. We show that cSOBER outperforms competitive baselines on diverse real-world blackbox-constrained problems, including safety-constrained drug discovery, and human-relationship-aware team optimisation over graph-structured space.

Bayesian Quadrature for Neural Ensemble Search

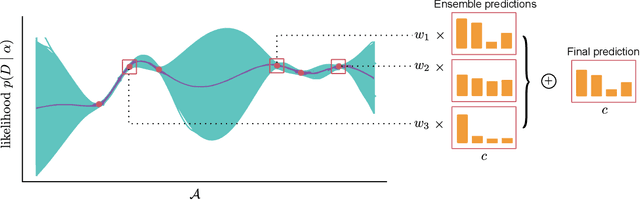
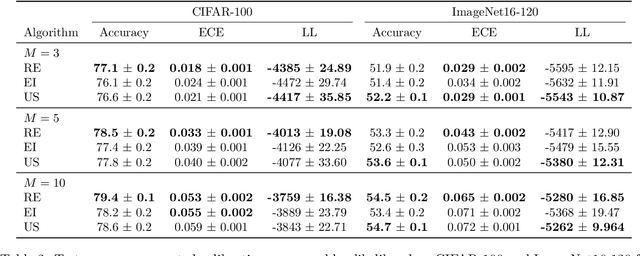
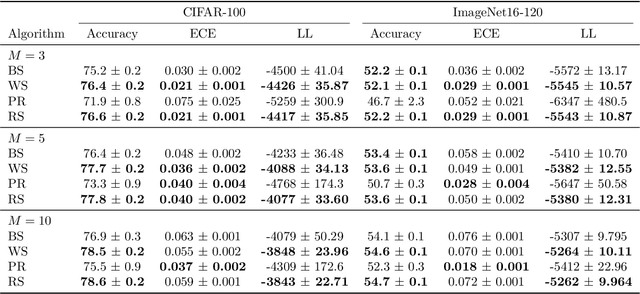
Ensembling can improve the performance of Neural Networks, but existing approaches struggle when the architecture likelihood surface has dispersed, narrow peaks. Furthermore, existing methods construct equally weighted ensembles, and this is likely to be vulnerable to the failure modes of the weaker architectures. By viewing ensembling as approximately marginalising over architectures we construct ensembles using the tools of Bayesian Quadrature -- tools which are well suited to the exploration of likelihood surfaces with dispersed, narrow peaks. Additionally, the resulting ensembles consist of architectures weighted commensurate with their performance. We show empirically -- in terms of test likelihood, accuracy, and expected calibration error -- that our method outperforms state-of-the-art baselines, and verify via ablation studies that its components do so independently.

SOBER: Scalable Batch Bayesian Optimization and Quadrature using Recombination Constraints

Batch Bayesian optimisation (BO) has shown to be a sample-efficient method of performing optimisation where expensive-to-evaluate objective functions can be queried in parallel. However, current methods do not scale to large batch sizes -- a frequent desideratum in practice (e.g. drug discovery or simulation-based inference). We present a novel algorithm, SOBER, which permits scalable and diversified batch BO with arbitrary acquisition functions, arbitrary input spaces (e.g. graph), and arbitrary kernels. The key to our approach is to reformulate batch selection for BO as a Bayesian quadrature (BQ) problem, which offers computational advantages. This reformulation is beneficial in solving BQ tasks reciprocally, which introduces the exploitative functionality of BO to BQ. We show that SOBER offers substantive performance gains in synthetic and real-world tasks, including drug discovery and simulation-based inference.

Fast Bayesian Inference with Batch Bayesian Quadrature via Kernel Recombination

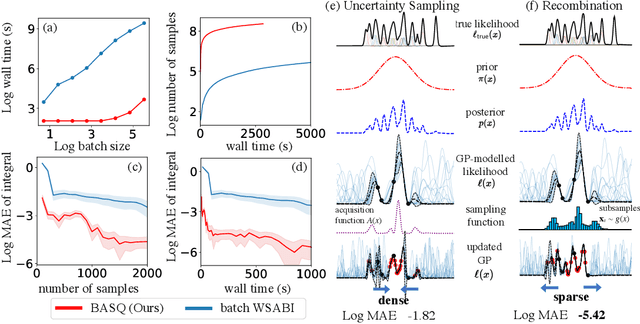
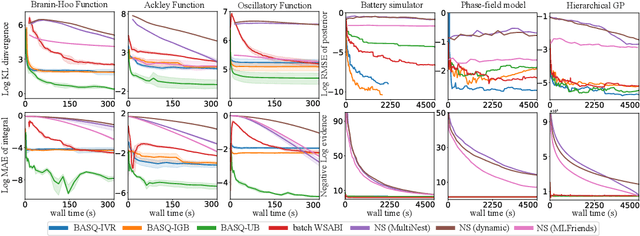
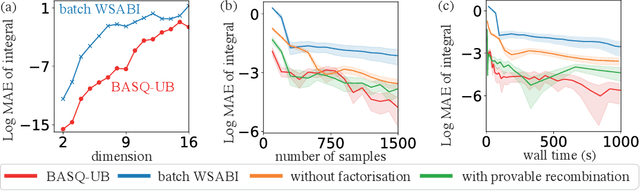
Calculation of Bayesian posteriors and model evidences typically requires numerical integration. Bayesian quadrature (BQ), a surrogate-model-based approach to numerical integration, is capable of superb sample efficiency, but its lack of parallelisation has hindered its practical applications. In this work, we propose a parallelised (batch) BQ method, employing techniques from kernel quadrature, that possesses a provably-exponential convergence rate. Additionally, just as with Nested Sampling, our method permits simultaneous inference of both posteriors and model evidence. Samples from our BQ surrogate model are re-selected to give a sparse set of samples, via a kernel recombination algorithm, requiring negligible additional time to increase the batch size. Empirically, we find that our approach significantly outperforms the sampling efficiency of both state-of-the-art BQ techniques and Nested Sampling in various real-world datasets, including lithium-ion battery analytics.

Last Layer Marginal Likelihood for Invariance Learning

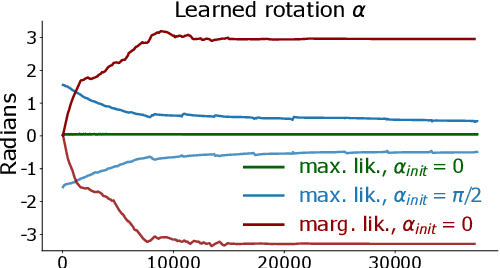
Data augmentation is often used to incorporate inductive biases into models. Traditionally, these are hand-crafted and tuned with cross validation. The Bayesian paradigm for model selection provides a path towards end-to-end learning of invariances using only the training data, by optimising the marginal likelihood. We work towards bringing this approach to neural networks by using an architecture with a Gaussian process in the last layer, a model for which the marginal likelihood can be computed. Experimentally, we improve performance by learning appropriate invariances in standard benchmarks, the low data regime and in a medical imaging task. Optimisation challenges for invariant Deep Kernel Gaussian processes are identified, and a systematic analysis is presented to arrive at a robust training scheme. We introduce a new lower bound to the marginal likelihood, which allows us to perform inference for a larger class of likelihood functions than before, thereby overcoming some of the training challenges that existed with previous approaches.

Bayesian Triplet Loss: Uncertainty Quantification in Image Retrieval

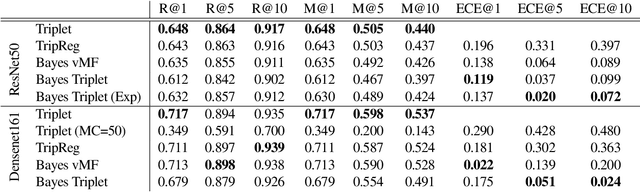
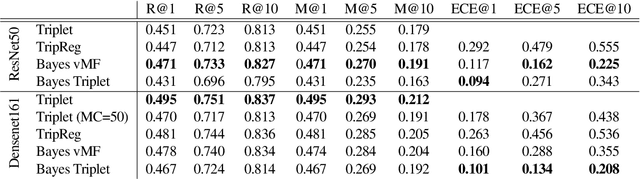
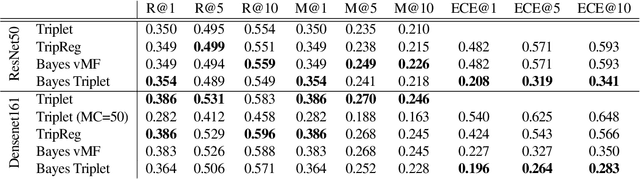
Uncertainty quantification in image retrieval is crucial for downstream decisions, yet it remains a challenging and largely unexplored problem. Current methods for estimating uncertainties are poorly calibrated, computationally expensive, or based on heuristics. We present a new method that views image embeddings as stochastic features rather than deterministic features. Our two main contributions are (1) a likelihood that matches the triplet constraint and that evaluates the probability of an anchor being closer to a positive than a negative; and (2) a prior over the feature space that justifies the conventional l2 normalization. To ensure computational efficiency, we derive a variational approximation of the posterior, called the Bayesian triplet loss, that produces state-of-the-art uncertainty estimates and matches the predictive performance of current state-of-the-art methods.

Reparametrization Invariance in non-parametric Causal Discovery

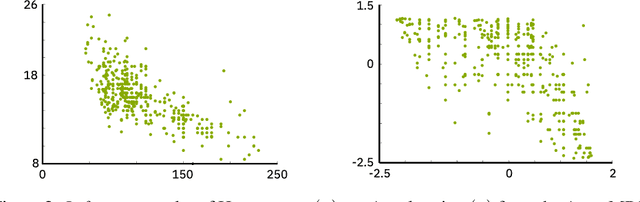
Causal discovery estimates the underlying physical process that generates the observed data: does X cause Y or does Y cause X? Current methodologies use structural conditions to turn the causal query into a statistical query, when only observational data is available. But what if these statistical queries are sensitive to causal invariants? This study investigates one such invariant: the causal relationship between X and Y is invariant to the marginal distributions of X and Y. We propose an algorithm that uses a non-parametric estimator that is robust to changes in the marginal distributions. This way we may marginalize the marginals, and inspect what relationship is intrinsically there. The resulting causal estimator is competitive with current methodologies and has high emphasis on the uncertainty in the causal query; an aspect just as important as the query itself.

Stochastic Differential Equations with Variational Wishart Diffusions

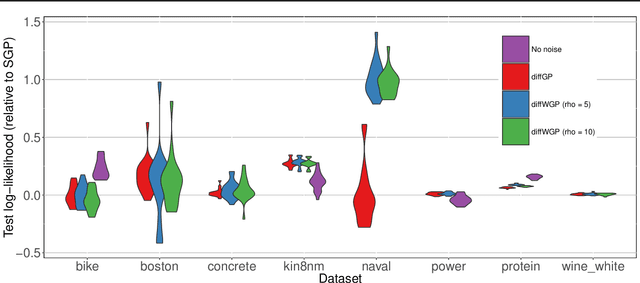
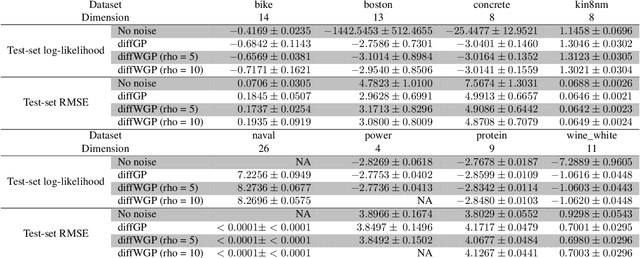
We present a Bayesian non-parametric way of inferring stochastic differential equations for both regression tasks and continuous-time dynamical modelling. The work has high emphasis on the stochastic part of the differential equation, also known as the diffusion, and modelling it by means of Wishart processes. Further, we present a semi-parametric approach that allows the framework to scale to high dimensions. This successfully lead us onto how to model both latent and auto-regressive temporal systems with conditional heteroskedastic noise. We provide experimental evidence that modelling diffusion often improves performance and that this randomness in the differential equation can be essential to avoid overfitting.

Isometric Gaussian Process Latent Variable Model for Dissimilarity Data

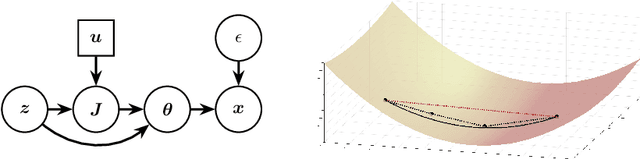
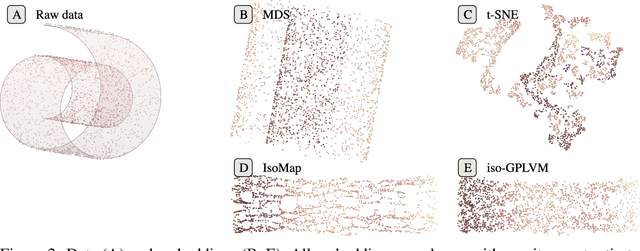
We propose a fully generative model where the latent variable respects both the distances and the topology of the modeled data. The model leverages the Riemannian geometry of the generated manifold to endow the latent space with a well-defined stochastic distance measure, which is modeled as Nakagami distributions. These stochastic distances are sought to be as similar as possible to observed distances along a neighborhood graph through a censoring process. The model is inferred by variational inference and is therefore fully generative. We demonstrate how the new model can encode invariances in the learned manifolds.