Stochastic Differential Equations with Variational Wishart Diffusions
Paper and Code
Jun 26, 2020

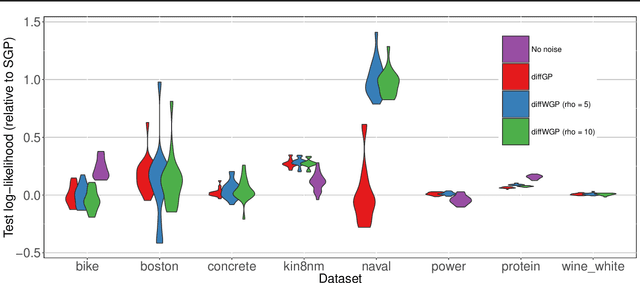
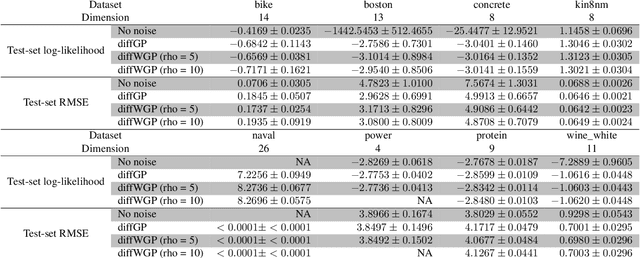
We present a Bayesian non-parametric way of inferring stochastic differential equations for both regression tasks and continuous-time dynamical modelling. The work has high emphasis on the stochastic part of the differential equation, also known as the diffusion, and modelling it by means of Wishart processes. Further, we present a semi-parametric approach that allows the framework to scale to high dimensions. This successfully lead us onto how to model both latent and auto-regressive temporal systems with conditional heteroskedastic noise. We provide experimental evidence that modelling diffusion often improves performance and that this randomness in the differential equation can be essential to avoid overfitting.
* ICML 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge