Bayesian Triplet Loss: Uncertainty Quantification in Image Retrieval
Paper and Code
Nov 25, 2020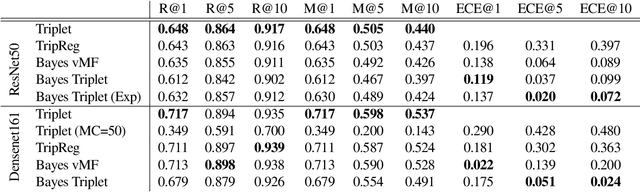
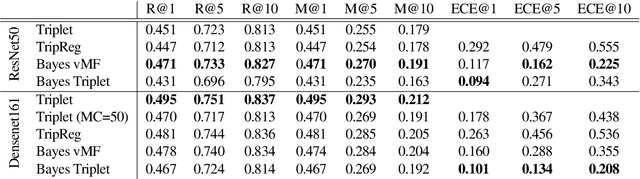
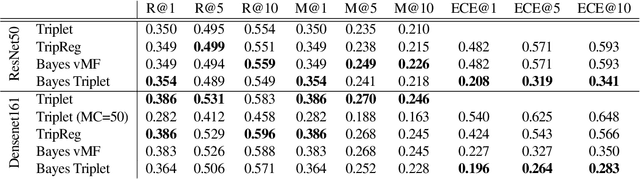
Uncertainty quantification in image retrieval is crucial for downstream decisions, yet it remains a challenging and largely unexplored problem. Current methods for estimating uncertainties are poorly calibrated, computationally expensive, or based on heuristics. We present a new method that views image embeddings as stochastic features rather than deterministic features. Our two main contributions are (1) a likelihood that matches the triplet constraint and that evaluates the probability of an anchor being closer to a positive than a negative; and (2) a prior over the feature space that justifies the conventional l2 normalization. To ensure computational efficiency, we derive a variational approximation of the posterior, called the Bayesian triplet loss, that produces state-of-the-art uncertainty estimates and matches the predictive performance of current state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge