Pola Elisabeth Schwöbel
Last Layer Marginal Likelihood for Invariance Learning
Jun 14, 2021


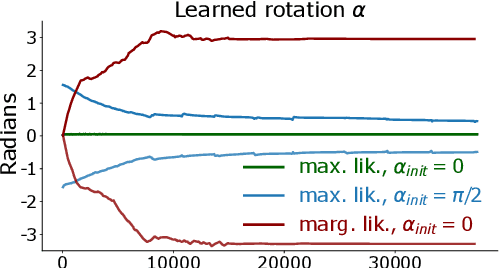
Abstract:Data augmentation is often used to incorporate inductive biases into models. Traditionally, these are hand-crafted and tuned with cross validation. The Bayesian paradigm for model selection provides a path towards end-to-end learning of invariances using only the training data, by optimising the marginal likelihood. We work towards bringing this approach to neural networks by using an architecture with a Gaussian process in the last layer, a model for which the marginal likelihood can be computed. Experimentally, we improve performance by learning appropriate invariances in standard benchmarks, the low data regime and in a medical imaging task. Optimisation challenges for invariant Deep Kernel Gaussian processes are identified, and a systematic analysis is presented to arrive at a robust training scheme. We introduce a new lower bound to the marginal likelihood, which allows us to perform inference for a larger class of likelihood functions than before, thereby overcoming some of the training challenges that existed with previous approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge