Bayesian Quadrature for Neural Ensemble Search
Paper and Code
Mar 17, 2023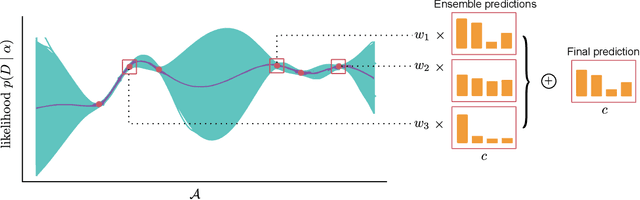

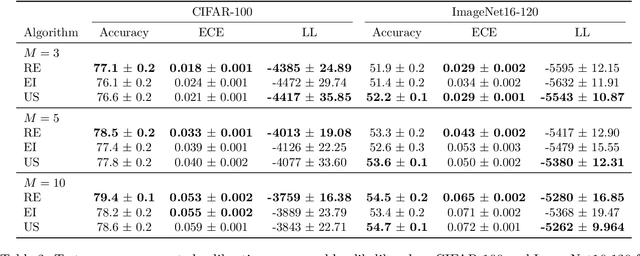
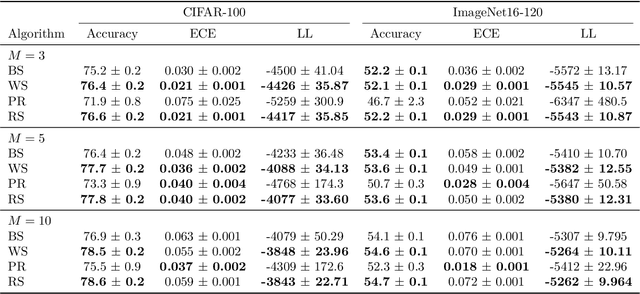
Ensembling can improve the performance of Neural Networks, but existing approaches struggle when the architecture likelihood surface has dispersed, narrow peaks. Furthermore, existing methods construct equally weighted ensembles, and this is likely to be vulnerable to the failure modes of the weaker architectures. By viewing ensembling as approximately marginalising over architectures we construct ensembles using the tools of Bayesian Quadrature -- tools which are well suited to the exploration of likelihood surfaces with dispersed, narrow peaks. Additionally, the resulting ensembles consist of architectures weighted commensurate with their performance. We show empirically -- in terms of test likelihood, accuracy, and expected calibration error -- that our method outperforms state-of-the-art baselines, and verify via ablation studies that its components do so independently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge