Advantage of Quantum Machine Learning from General Computational Advantages

An overarching milestone of quantum machine learning (QML) is to demonstrate the advantage of QML over all possible classical learning methods in accelerating a common type of learning task as represented by supervised learning with classical data. However, the provable advantages of QML in supervised learning have been known so far only for the learning tasks designed for using the advantage of specific quantum algorithms, i.e., Shor's algorithms. Here we explicitly construct an unprecedentedly broader family of supervised learning tasks with classical data to offer the provable advantage of QML based on general quantum computational advantages, progressing beyond Shor's algorithms. Our learning task is feasibly achievable by executing a general class of functions that can be computed efficiently in polynomial time for a large fraction of inputs by arbitrary quantum algorithms but not by any classical algorithm. We prove the hardness of achieving this learning task for any possible polynomial-time classical learning method. We also clarify protocols for preparing the classical data to demonstrate this learning task in experiments. These results open routes to exploit a variety of quantum advantages in computing functions for the experimental demonstration of the advantage of QML.

Quantum Ridgelet Transform: Winning Lottery Ticket of Neural Networks with Quantum Computation

Ridgelet transform has been a fundamental mathematical tool in the theoretical studies of neural networks. However, the practical applicability of ridgelet transform to conducting learning tasks was limited since its numerical implementation by conventional classical computation requires an exponential runtime $\exp(O(D))$ as data dimension $D$ increases. To address this problem, we develop a quantum ridgelet transform (QRT), which implements the ridgelet transform of a quantum state within a linear runtime $O(D)$ of quantum computation. As an application, we also show that one can use QRT as a fundamental subroutine for quantum machine learning (QML) to efficiently find a sparse trainable subnetwork of large shallow wide neural networks without conducting large-scale optimization of the original network. This application discovers an efficient way in this regime to demonstrate the lottery ticket hypothesis on finding such a sparse trainable neural network. These results open an avenue of QML for accelerating learning tasks with commonly used classical neural networks.

Stochastic Gradient Line Bayesian Optimization: Reducing Measurement Shots in Optimizing Parameterized Quantum Circuits

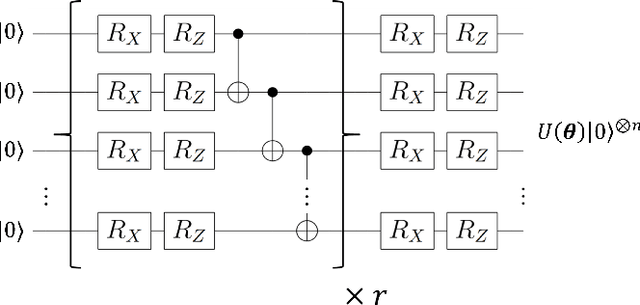
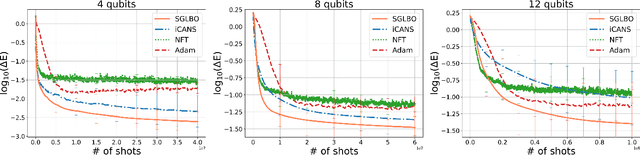
Optimization of parameterized quantum circuits is indispensable for applications of near-term quantum devices to computational tasks with variational quantum algorithms (VQAs). However, the existing optimization algorithms for VQAs require an excessive number of quantum-measurement shots in estimating expectation values of observables or iterating updates of circuit parameters, whose cost has been a crucial obstacle for practical use. To address this problem, we develop an efficient framework, \textit{stochastic gradient line Bayesian optimization} (SGLBO), for the circuit optimization with fewer measurement shots. The SGLBO reduces the cost of measurement shots by estimating an appropriate direction of updating the parameters based on stochastic gradient descent (SGD) and further by utilizing Bayesian optimization (BO) to estimate the optimal step size in each iteration of the SGD. We formulate an adaptive measurement-shot strategy to achieve the optimization feasibly without relying on precise expectation-value estimation and many iterations; moreover, we show that a technique of suffix averaging can significantly reduce the effect of statistical and hardware noise in the optimization for the VQAs. Our numerical simulation demonstrates that the SGLBO augmented with these techniques can drastically reduce the required number of measurement shots, improve the accuracy in the optimization, and enhance the robustness against the noise compared to other state-of-art optimizers in representative tasks for the VQAs. These results establish a framework of quantum-circuit optimizers integrating two different optimization approaches, SGD and BO, to reduce the cost of measurement shots significantly.

Exponential Error Convergence in Data Classification with Optimized Random Features: Acceleration by Quantum Machine Learning

Random features are a central technique for scalable learning algorithms based on kernel methods. A recent work has shown that an algorithm for machine learning by quantum computer, quantum machine learning (QML), can exponentially speed up sampling of optimized random features, even without imposing restrictive assumptions on sparsity and low-rankness of matrices that had limited applicability of conventional QML algorithms; this QML algorithm makes it possible to significantly reduce and provably minimize the required number of features for regression tasks. However, a major interest in the field of QML is how widely the advantages of quantum computation can be exploited, not only in the regression tasks. We here construct a QML algorithm for a classification task accelerated by the optimized random features. We prove that the QML algorithm for sampling optimized random features, combined with stochastic gradient descent (SGD), can achieve state-of-the-art exponential convergence speed of reducing classification error in a classification task under a low-noise condition; at the same time, our algorithm with optimized random features can take advantage of the significant reduction of the required number of features so as to accelerate each iteration in the SGD and evaluation of the classifier obtained from our algorithm. These results discover a promising application of QML to significant acceleration of the leading classification algorithm based on kernel methods, without ruining its applicability to a practical class of data sets and the exponential error-convergence speed.

Fast Quantum Algorithm for Learning with Optimized Random Features

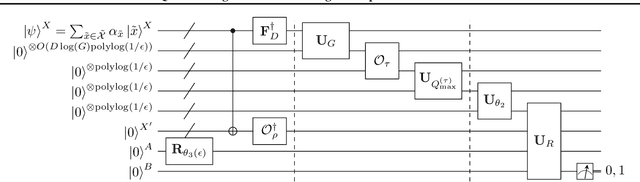
Kernel methods augmented with random features give scalable algorithms for learning from big data. But it has been computationally hard to sample random features according to a probability distribution that is optimized for the data, so as to minimize the required number of features for achieving the learning to a desired accuracy. Here, we develop a quantum algorithm for sampling from this optimized distribution over features, in runtime $O(D)$ that is linear in the dimension $D$ of the input data. Our algorithm achieves an exponential speedup in $D$ compared to any known classical algorithm for this sampling task. In contrast to existing quantum machine learning algorithms, our algorithm circumvents sparsity and low-rank assumptions and thus has wide applicability. We also show that the sampled features can be combined with regression by stochastic gradient descent to achieve the learning without canceling out our exponential speedup. Our algorithm based on sampling optimized random features leads to an accelerated framework for machine learning that takes advantage of quantum computers.