Stochastic Gradient Line Bayesian Optimization: Reducing Measurement Shots in Optimizing Parameterized Quantum Circuits
Paper and Code
Nov 15, 2021
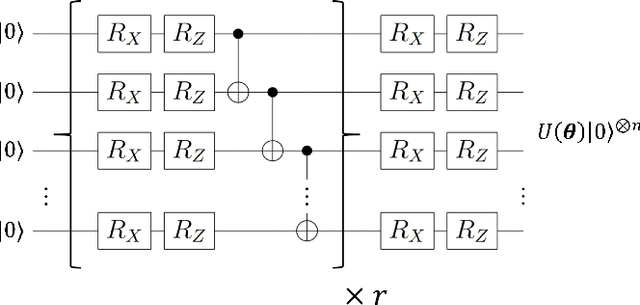
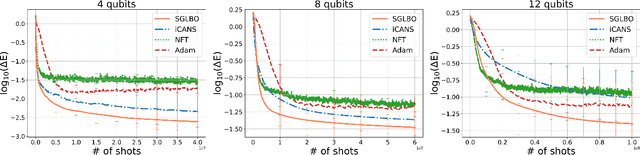

Optimization of parameterized quantum circuits is indispensable for applications of near-term quantum devices to computational tasks with variational quantum algorithms (VQAs). However, the existing optimization algorithms for VQAs require an excessive number of quantum-measurement shots in estimating expectation values of observables or iterating updates of circuit parameters, whose cost has been a crucial obstacle for practical use. To address this problem, we develop an efficient framework, \textit{stochastic gradient line Bayesian optimization} (SGLBO), for the circuit optimization with fewer measurement shots. The SGLBO reduces the cost of measurement shots by estimating an appropriate direction of updating the parameters based on stochastic gradient descent (SGD) and further by utilizing Bayesian optimization (BO) to estimate the optimal step size in each iteration of the SGD. We formulate an adaptive measurement-shot strategy to achieve the optimization feasibly without relying on precise expectation-value estimation and many iterations; moreover, we show that a technique of suffix averaging can significantly reduce the effect of statistical and hardware noise in the optimization for the VQAs. Our numerical simulation demonstrates that the SGLBO augmented with these techniques can drastically reduce the required number of measurement shots, improve the accuracy in the optimization, and enhance the robustness against the noise compared to other state-of-art optimizers in representative tasks for the VQAs. These results establish a framework of quantum-circuit optimizers integrating two different optimization approaches, SGD and BO, to reduce the cost of measurement shots significantly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge