Quantum Algorithms for Compositional Text Processing

Quantum computing and AI have found a fruitful intersection in the field of natural language processing. We focus on the recently proposed DisCoCirc framework for natural language, and propose a quantum adaptation, QDisCoCirc. This is motivated by a compositional approach to rendering AI interpretable: the behavior of the whole can be understood in terms of the behavior of parts, and the way they are put together. For the model-native primitive operation of text similarity, we derive quantum algorithms for fault-tolerant quantum computers to solve the task of question-answering within QDisCoCirc, and show that this is BQP-hard; note that we do not consider the complexity of question-answering in other natural language processing models. Assuming widely-held conjectures, implementing the proposed model classically would require super-polynomial resources. Therefore, it could provide a meaningful demonstration of the power of practical quantum processors. The model construction builds on previous work in compositional quantum natural language processing. Word embeddings are encoded as parameterized quantum circuits, and compositionality here means that the quantum circuits compose according to the linguistic structure of the text. We outline a method for evaluating the model on near-term quantum processors, and elsewhere we report on a recent implementation of this on quantum hardware. In addition, we adapt a quantum algorithm for the closest vector problem to obtain a Grover-like speedup in the fault-tolerant regime for our model. This provides an unconditional quadratic speedup over any classical algorithm in certain circumstances, which we will verify empirically in future work.

A Pattern Language for Machine Learning Tasks

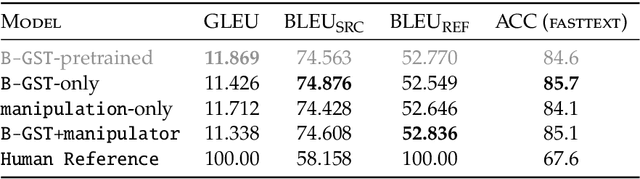
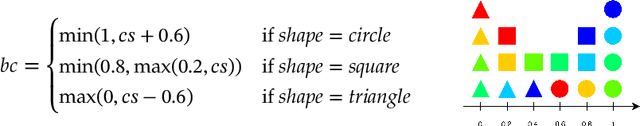
Idealised as universal approximators, learners such as neural networks can be viewed as "variable functions" that may become one of a range of concrete functions after training. In the same way that equations constrain the possible values of variables in algebra, we may view objective functions as constraints on the behaviour of learners. We extract the equivalences perfectly optimised objective functions impose, calling them "tasks". For these tasks, we develop a formal graphical language that allows us to: (1) separate the core tasks of a behaviour from its implementation details; (2) reason about and design behaviours model-agnostically; and (3) simply describe and unify approaches in machine learning across domains. As proof-of-concept, we design a novel task that enables converting classifiers into generative models we call "manipulators", which we implement by directly translating task specifications into code. The resulting models exhibit capabilities such as style transfer and interpretable latent-space editing, without the need for custom architectures, adversarial training or random sampling. We formally relate the behaviour of manipulators to GANs, and empirically demonstrate their competitive performance with VAEs. We report on experiments across vision and language domains aiming to characterise manipulators as approximate Bayesian inversions of discriminative classifiers.

On the Anatomy of Attention

We introduce a category-theoretic diagrammatic formalism in order to systematically relate and reason about machine learning models. Our diagrams present architectures intuitively but without loss of essential detail, where natural relationships between models are captured by graphical transformations, and important differences and similarities can be identified at a glance. In this paper, we focus on attention mechanisms: translating folklore into mathematical derivations, and constructing a taxonomy of attention variants in the literature. As a first example of an empirical investigation underpinned by our formalism, we identify recurring anatomical components of attention, which we exhaustively recombine to explore a space of variations on the attention mechanism.

Quantum Circuit Optimization with AlphaTensor

A key challenge in realizing fault-tolerant quantum computers is circuit optimization. Focusing on the most expensive gates in fault-tolerant quantum computation (namely, the T gates), we address the problem of T-count optimization, i.e., minimizing the number of T gates that are needed to implement a given circuit. To achieve this, we develop AlphaTensor-Quantum, a method based on deep reinforcement learning that exploits the relationship between optimizing T-count and tensor decomposition. Unlike existing methods for T-count optimization, AlphaTensor-Quantum can incorporate domain-specific knowledge about quantum computation and leverage gadgets, which significantly reduces the T-count of the optimized circuits. AlphaTensor-Quantum outperforms the existing methods for T-count optimization on a set of arithmetic benchmarks (even when compared without making use of gadgets). Remarkably, it discovers an efficient algorithm akin to Karatsuba's method for multiplication in finite fields. AlphaTensor-Quantum also finds the best human-designed solutions for relevant arithmetic computations used in Shor's algorithm and for quantum chemistry simulation, thus demonstrating it can save hundreds of hours of research by optimizing relevant quantum circuits in a fully automated way.