Eleni Sgouritsa
Max Planck Institute for Intelligent Systems
Evaluating Gemini in an arena for learning
May 30, 2025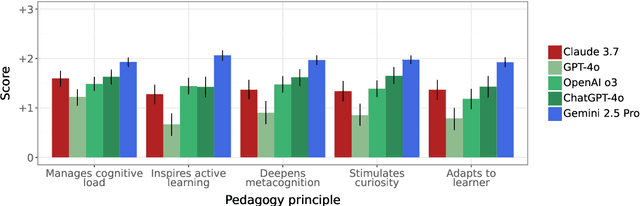

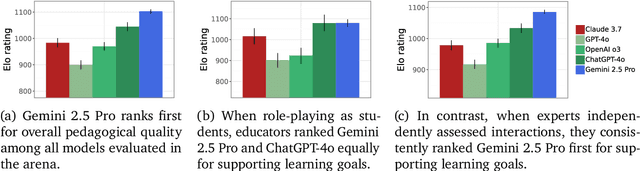
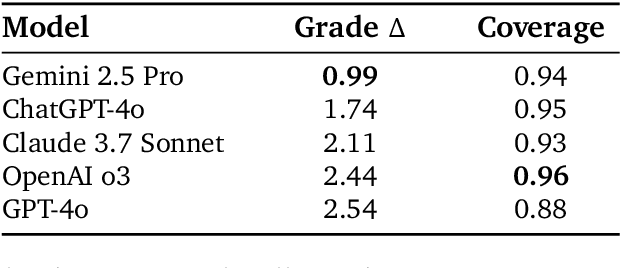
Abstract:Artificial intelligence (AI) is poised to transform education, but the research community lacks a robust, general benchmark to evaluate AI models for learning. To assess state-of-the-art support for educational use cases, we ran an "arena for learning" where educators and pedagogy experts conduct blind, head-to-head, multi-turn comparisons of leading AI models. In particular, $N = 189$ educators drew from their experience to role-play realistic learning use cases, interacting with two models sequentially, after which $N = 206$ experts judged which model better supported the user's learning goals. The arena evaluated a slate of state-of-the-art models: Gemini 2.5 Pro, Claude 3.7 Sonnet, GPT-4o, and OpenAI o3. Excluding ties, experts preferred Gemini 2.5 Pro in 73.2% of these match-ups -- ranking it first overall in the arena. Gemini 2.5 Pro also demonstrated markedly higher performance across key principles of good pedagogy. Altogether, these results position Gemini 2.5 Pro as a leading model for learning.
Prompting Strategies for Enabling Large Language Models to Infer Causation from Correlation
Dec 18, 2024



Abstract:The reasoning abilities of Large Language Models (LLMs) are attracting increasing attention. In this work, we focus on causal reasoning and address the task of establishing causal relationships based on correlation information, a highly challenging problem on which several LLMs have shown poor performance. We introduce a prompting strategy for this problem that breaks the original task into fixed subquestions, with each subquestion corresponding to one step of a formal causal discovery algorithm, the PC algorithm. The proposed prompting strategy, PC-SubQ, guides the LLM to follow these algorithmic steps, by sequentially prompting it with one subquestion at a time, augmenting the next subquestion's prompt with the answer to the previous one(s). We evaluate our approach on an existing causal benchmark, Corr2Cause: our experiments indicate a performance improvement across five LLMs when comparing PC-SubQ to baseline prompting strategies. Results are robust to causal query perturbations, when modifying the variable names or paraphrasing the expressions.
FunBO: Discovering Acquisition Functions for Bayesian Optimization with FunSearch
Jun 07, 2024



Abstract:The sample efficiency of Bayesian optimization algorithms depends on carefully crafted acquisition functions (AFs) guiding the sequential collection of function evaluations. The best-performing AF can vary significantly across optimization problems, often requiring ad-hoc and problem-specific choices. This work tackles the challenge of designing novel AFs that perform well across a variety of experimental settings. Based on FunSearch, a recent work using Large Language Models (LLMs) for discovery in mathematical sciences, we propose FunBO, an LLM-based method that can be used to learn new AFs written in computer code by leveraging access to a limited number of evaluations for a set of objective functions. We provide the analytic expression of all discovered AFs and evaluate them on various global optimization benchmarks and hyperparameter optimization tasks. We show how FunBO identifies AFs that generalize well in and out of the training distribution of functions, thus outperforming established general-purpose AFs and achieving competitive performance against AFs that are customized to specific function types and are learned via transfer-learning algorithms.
Consistency of Causal Inference under the Additive Noise Model
Feb 05, 2014

Abstract:We analyze a family of methods for statistical causal inference from sample under the so-called Additive Noise Model. While most work on the subject has concentrated on establishing the soundness of the Additive Noise Model, the statistical consistency of the resulting inference methods has received little attention. We derive general conditions under which the given family of inference methods consistently infers the causal direction in a nonparametric setting.
Identifying Finite Mixtures of Nonparametric Product Distributions and Causal Inference of Confounders
Sep 26, 2013



Abstract:We propose a kernel method to identify finite mixtures of nonparametric product distributions. It is based on a Hilbert space embedding of the joint distribution. The rank of the constructed tensor is equal to the number of mixture components. We present an algorithm to recover the components by partitioning the data points into clusters such that the variables are jointly conditionally independent given the cluster. This method can be used to identify finite confounders.
On Causal and Anticausal Learning
Jun 27, 2012



Abstract:We consider the problem of function estimation in the case where an underlying causal model can be inferred. This has implications for popular scenarios such as covariate shift, concept drift, transfer learning and semi-supervised learning. We argue that causal knowledge may facilitate some approaches for a given problem, and rule out others. In particular, we formulate a hypothesis for when semi-supervised learning can help, and corroborate it with empirical results.
Detecting low-complexity unobserved causes
Feb 14, 2012



Abstract:We describe a method that infers whether statistical dependences between two observed variables X and Y are due to a "direct" causal link or only due to a connecting causal path that contains an unobserved variable of low complexity, e.g., a binary variable. This problem is motivated by statistical genetics. Given a genetic marker that is correlated with a phenotype of interest, we want to detect whether this marker is causal or it only correlates with a causal one. Our method is based on the analysis of the location of the conditional distributions P(Y|x) in the simplex of all distributions of Y. We report encouraging results on semi-empirical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge