An Efficient Variant of One-Class SVM with Lifelong Online Learning Guarantees

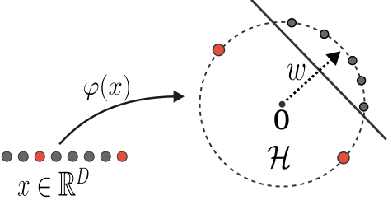
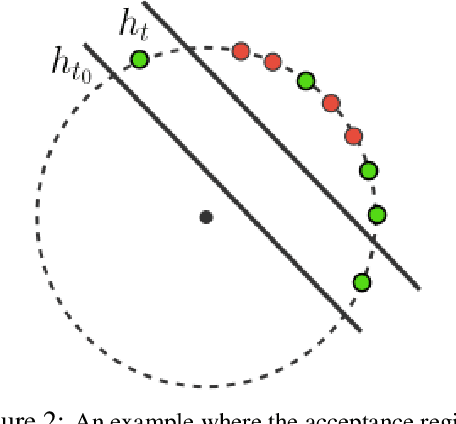
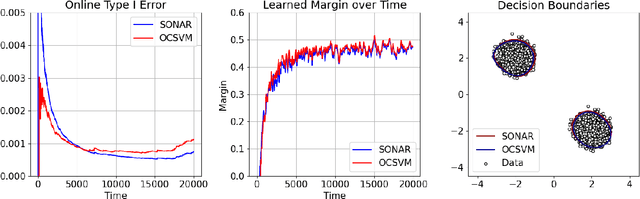
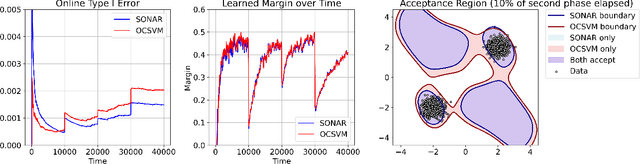
We study outlier (a.k.a., anomaly) detection for single-pass non-stationary streaming data. In the well-studied offline or batch outlier detection problem, traditional methods such as kernel One-Class SVM (OCSVM) are both computationally heavy and prone to large false-negative (Type II) errors under non-stationarity. To remedy this, we introduce SONAR, an efficient SGD-based OCSVM solver with strongly convex regularization. We show novel theoretical guarantees on the Type I/II errors of SONAR, superior to those known for OCSVM, and further prove that SONAR ensures favorable lifelong learning guarantees under benign distribution shifts. In the more challenging problem of adversarial non-stationary data, we show that SONAR can be used within an ensemble method and equipped with changepoint detection to achieve adaptive guarantees, ensuring small Type I/II errors on each phase of data. We validate our theoretical findings on synthetic and real-world datasets.

Neyman-Pearson Classification under Both Null and Alternative Distributions Shift

We consider the problem of transfer learning in Neyman-Pearson classification, where the objective is to minimize the error w.r.t. a distribution $μ_1$, subject to the constraint that the error w.r.t. a distribution $μ_0$ remains below a prescribed threshold. While transfer learning has been extensively studied in traditional classification, transfer learning in imbalanced classification such as Neyman-Pearson classification has received much less attention. This setting poses unique challenges, as both types of errors must be simultaneously controlled. Existing works address only the case of distribution shift in $μ_1$, whereas in many practical scenarios shifts may occur in both $μ_0$ and $μ_1$. We derive an adaptive procedure that not only guarantees improved Type-I and Type-II errors when the source is informative, but also automatically adapt to situations where the source is uninformative, thereby avoiding negative transfer. In addition to such statistical guarantees, the procedures is efficient, as shown via complementary computational guarantees.

Distributionally-Constrained Adversaries in Online Learning

There has been much recent interest in understanding the continuum from adversarial to stochastic settings in online learning, with various frameworks including smoothed settings proposed to bridge this gap. We consider the more general and flexible framework of distributionally constrained adversaries in which instances are drawn from distributions chosen by an adversary within some constrained distribution class [RST11]. Compared to smoothed analysis, we consider general distributional classes which allows for a fine-grained understanding of learning settings between fully stochastic and fully adversarial for which a learner can achieve non-trivial regret. We give a characterization for which distribution classes are learnable in this context against both oblivious and adaptive adversaries, providing insights into the types of interplay between the function class and distributional constraints on adversaries that enable learnability. In particular, our results recover and generalize learnability for known smoothed settings. Further, we show that for several natural function classes including linear classifiers, learning can be achieved without any prior knowledge of the distribution class -- in other words, a learner can simultaneously compete against any constrained adversary within learnable distribution classes.

Transfer Neyman-Pearson Algorithm for Outlier Detection

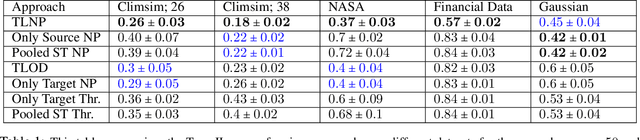
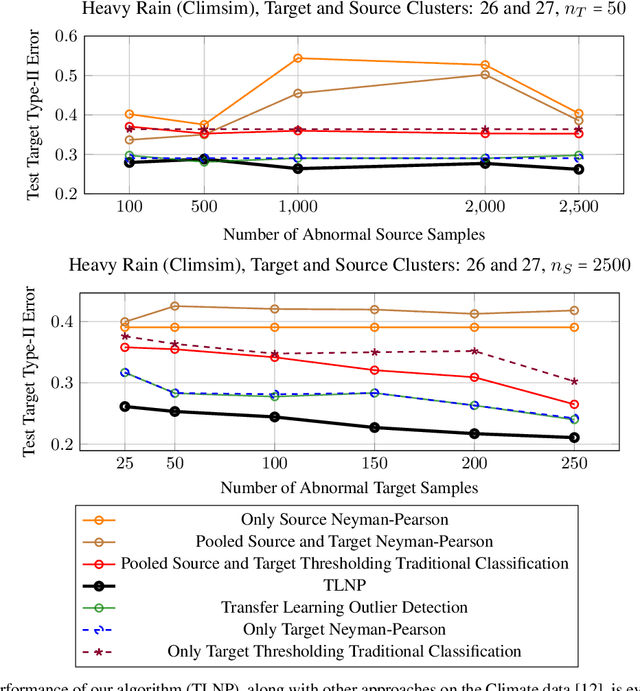
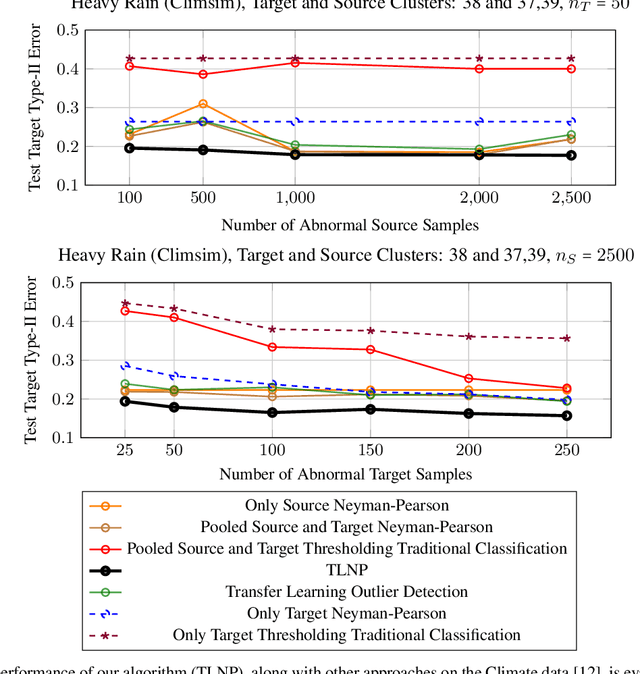
We consider the problem of transfer learning in outlier detection where target abnormal data is rare. While transfer learning has been considered extensively in traditional balanced classification, the problem of transfer in outlier detection and more generally in imbalanced classification settings has received less attention. We propose a general meta-algorithm which is shown theoretically to yield strong guarantees w.r.t. to a range of changes in abnormal distribution, and at the same time amenable to practical implementation. We then investigate different instantiations of this general meta-algorithm, e.g., based on multi-layer neural networks, and show empirically that they outperform natural extensions of transfer methods for traditional balanced classification settings (which are the only solutions available at the moment).

A More Unified Theory of Transfer Learning

We show that some basic moduli of continuity $\delta$ -- which measure how fast target risk decreases as source risk decreases -- appear to be at the root of many of the classical relatedness measures in transfer learning and related literature. Namely, bounds in terms of $\delta$ recover many of the existing bounds in terms of other measures of relatedness -- both in regression and classification -- and can at times be tighter. We are particularly interested in general situations where the learner has access to both source data and some or no target data. The unified perspective allowed by the moduli $\delta$ allow us to extend many existing notions of relatedness at once to these scenarios involving target data: interestingly, while $\delta$ itself might not be efficiently estimated, adaptive procedures exist -- based on reductions to confidence sets -- which can get nearly tight rates in terms of $\delta$ with no prior distributional knowledge. Such adaptivity to unknown $\delta$ immediately implies adaptivity to many classical relatedness notions, in terms of combined source and target samples' sizes.

Distribution-Free Rates in Neyman-Pearson Classification

We consider the problem of Neyman-Pearson classification which models unbalanced classification settings where error w.r.t. a distribution $\mu_1$ is to be minimized subject to low error w.r.t. a different distribution $\mu_0$. Given a fixed VC class $\mathcal{H}$ of classifiers to be minimized over, we provide a full characterization of possible distribution-free rates, i.e., minimax rates over the space of all pairs $(\mu_0, \mu_1)$. The rates involve a dichotomy between hard and easy classes $\mathcal{H}$ as characterized by a simple geometric condition, a three-points-separation condition, loosely related to VC dimension.

Efficient Estimation of the Central Mean Subspace via Smoothed Gradient Outer Products

We consider the problem of sufficient dimension reduction (SDR) for multi-index models. The estimators of the central mean subspace in prior works either have slow (non-parametric) convergence rates, or rely on stringent distributional conditions (e.g., the covariate distribution $P_{\mathbf{X}}$ being elliptical symmetric). In this paper, we show that a fast parametric convergence rate of form $C_d \cdot n^{-1/2}$ is achievable via estimating the \emph{expected smoothed gradient outer product}, for a general class of distribution $P_{\mathbf{X}}$ admitting Gaussian or heavier distributions. When the link function is a polynomial with a degree of at most $r$ and $P_{\mathbf{X}}$ is the standard Gaussian, we show that the prefactor depends on the ambient dimension $d$ as $C_d \propto d^r$.

Tight Rates in Supervised Outlier Transfer Learning

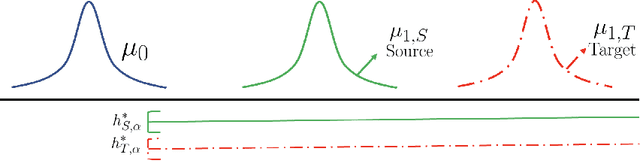
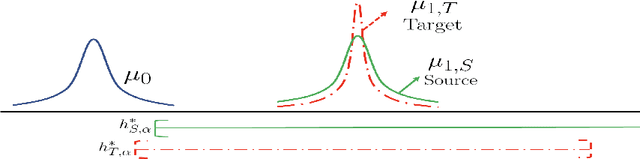
A critical barrier to learning an accurate decision rule for outlier detection is the scarcity of outlier data. As such, practitioners often turn to the use of similar but imperfect outlier data from which they might transfer information to the target outlier detection task. Despite the recent empirical success of transfer learning approaches in outlier detection, a fundamental understanding of when and how knowledge can be transferred from a source to a target outlier detection task remains elusive. In this work, we adopt the traditional framework of Neyman-Pearson classification -- which formalizes supervised outlier detection -- with the added assumption that one has access to some related but imperfect outlier data. Our main results are as follows: We first determine the information-theoretic limits of the problem under a measure of discrepancy that extends some existing notions from traditional balanced classification; interestingly, unlike in balanced classification, seemingly very dissimilar sources can provide much information about a target, thus resulting in fast transfer. We then show that, in principle, these information-theoretic limits are achievable by adaptive procedures, i.e., procedures with no a priori information on the discrepancy between source and target outlier distributions.

Nonlinear Meta-Learning Can Guarantee Faster Rates

Many recent theoretical works on \emph{meta-learning} aim to achieve guarantees in leveraging similar representational structures from related tasks towards simplifying a target task. Importantly, the main aim in theory works on the subject is to understand the extent to which convergence rates -- in learning a common representation -- \emph{may scale with the number $N$ of tasks} (as well as the number of samples per task). First steps in this setting demonstrate this property when both the shared representation amongst tasks, and task-specific regression functions, are linear. This linear setting readily reveals the benefits of aggregating tasks, e.g., via averaging arguments. In practice, however, the representation is often highly nonlinear, introducing nontrivial biases in each task that cannot easily be averaged out as in the linear case. In the present work, we derive theoretical guarantees for meta-learning with nonlinear representations. In particular, assuming the shared nonlinearity maps to an infinite-dimensional RKHS, we show that additional biases can be mitigated with careful regularization that leverages the smoothness of task-specific regression functions,

Tracking Most Significant Shifts in Nonparametric Contextual Bandits

We study nonparametric contextual bandits where Lipschitz mean reward functions may change over time. We first establish the minimax dynamic regret rate in this less understood setting in terms of number of changes $L$ and total-variation $V$, both capturing all changes in distribution over context space, and argue that state-of-the-art procedures are suboptimal in this setting. Next, we tend to the question of an adaptivity for this setting, i.e. achieving the minimax rate without knowledge of $L$ or $V$. Quite importantly, we posit that the bandit problem, viewed locally at a given context $X_t$, should not be affected by reward changes in other parts of context space $\cal X$. We therefore propose a notion of change, which we term experienced significant shifts, that better accounts for locality, and thus counts considerably less changes than $L$ and $V$. Furthermore, similar to recent work on non-stationary MAB (Suk & Kpotufe, 2022), experienced significant shifts only count the most significant changes in mean rewards, e.g., severe best-arm changes relevant to observed contexts. Our main result is to show that this more tolerant notion of change can in fact be adapted to.