Neyman-Pearson Classification under Both Null and Alternative Distributions Shift

We consider the problem of transfer learning in Neyman-Pearson classification, where the objective is to minimize the error w.r.t. a distribution $μ_1$, subject to the constraint that the error w.r.t. a distribution $μ_0$ remains below a prescribed threshold. While transfer learning has been extensively studied in traditional classification, transfer learning in imbalanced classification such as Neyman-Pearson classification has received much less attention. This setting poses unique challenges, as both types of errors must be simultaneously controlled. Existing works address only the case of distribution shift in $μ_1$, whereas in many practical scenarios shifts may occur in both $μ_0$ and $μ_1$. We derive an adaptive procedure that not only guarantees improved Type-I and Type-II errors when the source is informative, but also automatically adapt to situations where the source is uninformative, thereby avoiding negative transfer. In addition to such statistical guarantees, the procedures is efficient, as shown via complementary computational guarantees.

Concentration and excess risk bounds for imbalanced classification with synthetic oversampling

Synthetic oversampling of minority examples using SMOTE and its variants is a leading strategy for addressing imbalanced classification problems. Despite the success of this approach in practice, its theoretical foundations remain underexplored. We develop a theoretical framework to analyze the behavior of SMOTE and related methods when classifiers are trained on synthetic data. We first derive a uniform concentration bound on the discrepancy between the empirical risk over synthetic minority samples and the population risk on the true minority distribution. We then provide a nonparametric excess risk guarantee for kernel-based classifiers trained using such synthetic data. These results lead to practical guidelines for better parameter tuning of both SMOTE and the downstream learning algorithm. Numerical experiments are provided to illustrate and support the theoretical findings

Transfer Neyman-Pearson Algorithm for Outlier Detection

We consider the problem of transfer learning in outlier detection where target abnormal data is rare. While transfer learning has been considered extensively in traditional balanced classification, the problem of transfer in outlier detection and more generally in imbalanced classification settings has received less attention. We propose a general meta-algorithm which is shown theoretically to yield strong guarantees w.r.t. to a range of changes in abnormal distribution, and at the same time amenable to practical implementation. We then investigate different instantiations of this general meta-algorithm, e.g., based on multi-layer neural networks, and show empirically that they outperform natural extensions of transfer methods for traditional balanced classification settings (which are the only solutions available at the moment).

Distribution-Free Rates in Neyman-Pearson Classification

We consider the problem of Neyman-Pearson classification which models unbalanced classification settings where error w.r.t. a distribution $\mu_1$ is to be minimized subject to low error w.r.t. a different distribution $\mu_0$. Given a fixed VC class $\mathcal{H}$ of classifiers to be minimized over, we provide a full characterization of possible distribution-free rates, i.e., minimax rates over the space of all pairs $(\mu_0, \mu_1)$. The rates involve a dichotomy between hard and easy classes $\mathcal{H}$ as characterized by a simple geometric condition, a three-points-separation condition, loosely related to VC dimension.

Tight Rates in Supervised Outlier Transfer Learning

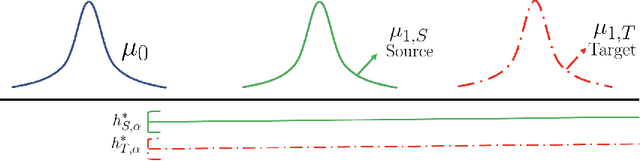
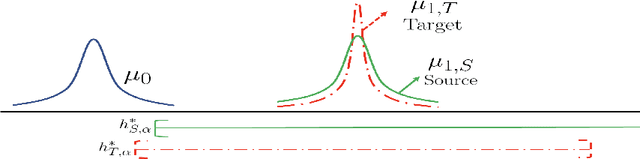
A critical barrier to learning an accurate decision rule for outlier detection is the scarcity of outlier data. As such, practitioners often turn to the use of similar but imperfect outlier data from which they might transfer information to the target outlier detection task. Despite the recent empirical success of transfer learning approaches in outlier detection, a fundamental understanding of when and how knowledge can be transferred from a source to a target outlier detection task remains elusive. In this work, we adopt the traditional framework of Neyman-Pearson classification -- which formalizes supervised outlier detection -- with the added assumption that one has access to some related but imperfect outlier data. Our main results are as follows: We first determine the information-theoretic limits of the problem under a measure of discrepancy that extends some existing notions from traditional balanced classification; interestingly, unlike in balanced classification, seemingly very dissimilar sources can provide much information about a target, thus resulting in fast transfer. We then show that, in principle, these information-theoretic limits are achievable by adaptive procedures, i.e., procedures with no a priori information on the discrepancy between source and target outlier distributions.