BIG-Bench Extra Hard

Large language models (LLMs) are increasingly deployed in everyday applications, demanding robust general reasoning capabilities and diverse reasoning skillset. However, current LLM reasoning benchmarks predominantly focus on mathematical and coding abilities, leaving a gap in evaluating broader reasoning proficiencies. One particular exception is the BIG-Bench dataset, which has served as a crucial benchmark for evaluating the general reasoning capabilities of LLMs, thanks to its diverse set of challenging tasks that allowed for a comprehensive assessment of general reasoning across various skills within a unified framework. However, recent advances in LLMs have led to saturation on BIG-Bench, and its harder version BIG-Bench Hard (BBH). State-of-the-art models achieve near-perfect scores on many tasks in BBH, thus diminishing its utility. To address this limitation, we introduce BIG-Bench Extra Hard (BBEH), a new benchmark designed to push the boundaries of LLM reasoning evaluation. BBEH replaces each task in BBH with a novel task that probes a similar reasoning capability but exhibits significantly increased difficulty. We evaluate various models on BBEH and observe a (harmonic) average accuracy of 9.8\% for the best general-purpose model and 44.8\% for the best reasoning-specialized model, indicating substantial room for improvement and highlighting the ongoing challenge of achieving robust general reasoning in LLMs. We release BBEH publicly at: https://github.com/google-deepmind/bbeh.

Prompting Strategies for Enabling Large Language Models to Infer Causation from Correlation

The reasoning abilities of Large Language Models (LLMs) are attracting increasing attention. In this work, we focus on causal reasoning and address the task of establishing causal relationships based on correlation information, a highly challenging problem on which several LLMs have shown poor performance. We introduce a prompting strategy for this problem that breaks the original task into fixed subquestions, with each subquestion corresponding to one step of a formal causal discovery algorithm, the PC algorithm. The proposed prompting strategy, PC-SubQ, guides the LLM to follow these algorithmic steps, by sequentially prompting it with one subquestion at a time, augmenting the next subquestion's prompt with the answer to the previous one(s). We evaluate our approach on an existing causal benchmark, Corr2Cause: our experiments indicate a performance improvement across five LLMs when comparing PC-SubQ to baseline prompting strategies. Results are robust to causal query perturbations, when modifying the variable names or paraphrasing the expressions.

Mind the Graph When Balancing Data for Fairness or Robustness

Failures of fairness or robustness in machine learning predictive settings can be due to undesired dependencies between covariates, outcomes and auxiliary factors of variation. A common strategy to mitigate these failures is data balancing, which attempts to remove those undesired dependencies. In this work, we define conditions on the training distribution for data balancing to lead to fair or robust models. Our results display that, in many cases, the balanced distribution does not correspond to selectively removing the undesired dependencies in a causal graph of the task, leading to multiple failure modes and even interference with other mitigation techniques such as regularization. Overall, our results highlight the importance of taking the causal graph into account before performing data balancing.

FunBO: Discovering Acquisition Functions for Bayesian Optimization with FunSearch

The sample efficiency of Bayesian optimization algorithms depends on carefully crafted acquisition functions (AFs) guiding the sequential collection of function evaluations. The best-performing AF can vary significantly across optimization problems, often requiring ad-hoc and problem-specific choices. This work tackles the challenge of designing novel AFs that perform well across a variety of experimental settings. Based on FunSearch, a recent work using Large Language Models (LLMs) for discovery in mathematical sciences, we propose FunBO, an LLM-based method that can be used to learn new AFs written in computer code by leveraging access to a limited number of evaluations for a set of objective functions. We provide the analytic expression of all discovered AFs and evaluate them on various global optimization benchmarks and hyperparameter optimization tasks. We show how FunBO identifies AFs that generalize well in and out of the training distribution of functions, thus outperforming established general-purpose AFs and achieving competitive performance against AFs that are customized to specific function types and are learned via transfer-learning algorithms.

Additive Causal Bandits with Unknown Graph

We explore algorithms to select actions in the causal bandit setting where the learner can choose to intervene on a set of random variables related by a causal graph, and the learner sequentially chooses interventions and observes a sample from the interventional distribution. The learner's goal is to quickly find the intervention, among all interventions on observable variables, that maximizes the expectation of an outcome variable. We depart from previous literature by assuming no knowledge of the causal graph except that latent confounders between the outcome and its ancestors are not present. We first show that the unknown graph problem can be exponentially hard in the parents of the outcome. To remedy this, we adopt an additional additive assumption on the outcome which allows us to solve the problem by casting it as an additive combinatorial linear bandit problem with full-bandit feedback. We propose a novel action-elimination algorithm for this setting, show how to apply this algorithm to the causal bandit problem, provide sample complexity bounds, and empirically validate our findings on a suite of randomly generated causal models, effectively showing that one does not need to explicitly learn the parents of the outcome to identify the best intervention.

Functional Causal Bayesian Optimization

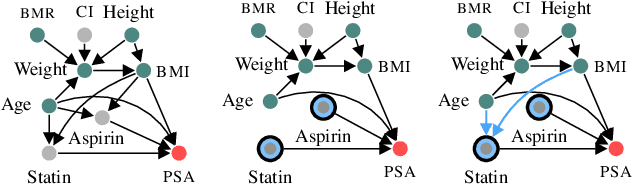
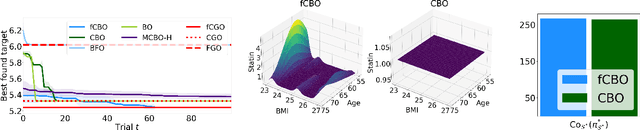
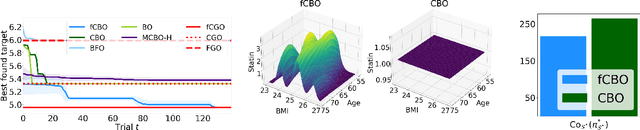
We propose functional causal Bayesian optimization (fCBO), a method for finding interventions that optimize a target variable in a known causal graph. fCBO extends the CBO family of methods to enable functional interventions, which set a variable to be a deterministic function of other variables in the graph. fCBO models the unknown objectives with Gaussian processes whose inputs are defined in a reproducing kernel Hilbert space, thus allowing to compute distances among vector-valued functions. In turn, this enables to sequentially select functions to explore by maximizing an expected improvement acquisition functional while keeping the typical computational tractability of standard BO settings. We introduce graphical criteria that establish when considering functional interventions allows attaining better target effects, and conditions under which selected interventions are also optimal for conditional target effects. We demonstrate the benefits of the method in a synthetic and in a real-world causal graph.

Constrained Causal Bayesian Optimization

We propose constrained causal Bayesian optimization (cCBO), an approach for finding interventions in a known causal graph that optimize a target variable under some constraints. cCBO first reduces the search space by exploiting the graph structure and, if available, an observational dataset; and then solves the restricted optimization problem by modelling target and constraint quantities using Gaussian processes and by sequentially selecting interventions via a constrained expected improvement acquisition function. We propose different surrogate models that enable to integrate observational and interventional data while capturing correlation among effects with increasing levels of sophistication. We evaluate cCBO on artificial and real-world causal graphs showing successful trade off between fast convergence and percentage of feasible interventions.

DiscoGen: Learning to Discover Gene Regulatory Networks

Accurately inferring Gene Regulatory Networks (GRNs) is a critical and challenging task in biology. GRNs model the activatory and inhibitory interactions between genes and are inherently causal in nature. To accurately identify GRNs, perturbational data is required. However, most GRN discovery methods only operate on observational data. Recent advances in neural network-based causal discovery methods have significantly improved causal discovery, including handling interventional data, improvements in performance and scalability. However, applying state-of-the-art (SOTA) causal discovery methods in biology poses challenges, such as noisy data and a large number of samples. Thus, adapting the causal discovery methods is necessary to handle these challenges. In this paper, we introduce DiscoGen, a neural network-based GRN discovery method that can denoise gene expression measurements and handle interventional data. We demonstrate that our model outperforms SOTA neural network-based causal discovery methods.

Pragmatic Fairness: Developing Policies with Outcome Disparity Control

We introduce a causal framework for designing optimal policies that satisfy fairness constraints. We take a pragmatic approach asking what we can do with an action space available to us and only with access to historical data. We propose two different fairness constraints: a moderation breaking constraint which aims at blocking moderation paths from the action and sensitive attribute to the outcome, and by that at reducing disparity in outcome levels as much as the provided action space permits; and an equal benefit constraint which aims at distributing gain from the new and maximized policy equally across sensitive attribute levels, and thus at keeping pre-existing preferential treatment in place or avoiding the introduction of new disparity. We introduce practical methods for implementing the constraints and illustrate their uses on experiments with semi-synthetic models.

Learning to Induce Causal Structure

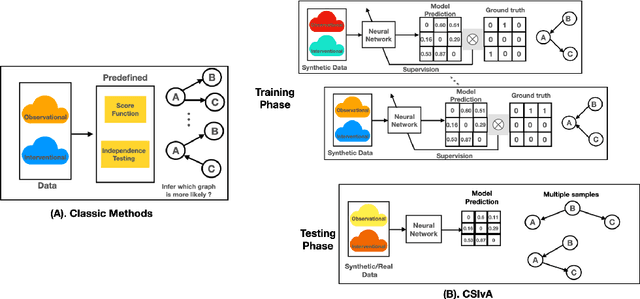
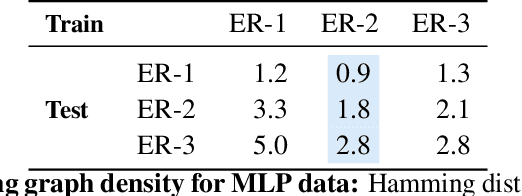
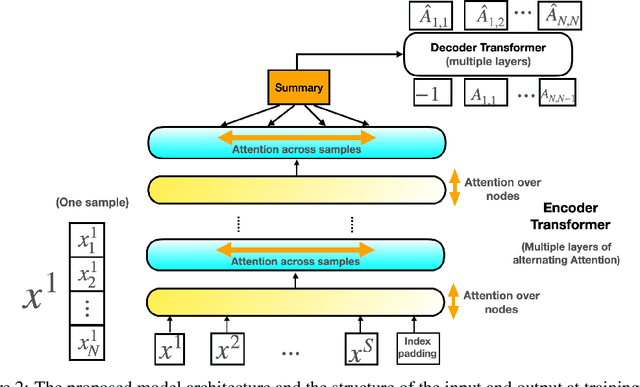
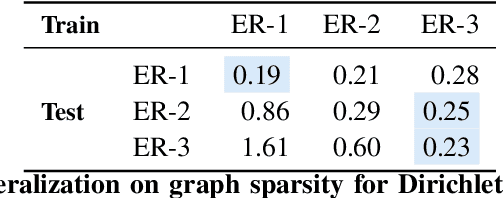
The fundamental challenge in causal induction is to infer the underlying graph structure given observational and/or interventional data. Most existing causal induction algorithms operate by generating candidate graphs and then evaluating them using either score-based methods (including continuous optimization) or independence tests. In this work, instead of proposing scoring function or independence tests, we treat the inference process as a black box and design a neural network architecture that learns the mapping from both observational and interventional data to graph structures via supervised training on synthetic graphs. We show that the proposed model generalizes not only to new synthetic graphs but also to naturalistic graphs.