Frontier LLMs Still Struggle with Simple Reasoning Tasks

While state-of-the-art large language models (LLMs) demonstrate advanced reasoning capabilities-achieving remarkable performance on challenging competitive math and coding benchmarks-they also frequently fail on tasks that are easy for humans. This work studies the performance of frontier LLMs on a broad set of such "easy" reasoning problems. By extending previous work in the literature, we create a suite of procedurally generated simple reasoning tasks, including counting, first-order logic, proof trees, and travel planning, with changeable parameters (such as document length. or the number of variables in a math problem) that can arbitrarily increase the amount of computation required to produce the answer while preserving the fundamental difficulty. While previous work showed that traditional, non-thinking models can be made to fail on such problems, we demonstrate that even state-of-the-art thinking models consistently fail on such problems and for similar reasons (e.g. statistical shortcuts, errors in intermediate steps, and difficulties in processing long contexts). To further understand the behavior of the models, we introduce the unpuzzles dataset, a different "easy" benchmark consisting of trivialized versions of well-known math and logic puzzles. Interestingly, while modern LLMs excel at solving the original puzzles, they tend to fail on the trivialized versions, exhibiting several systematic failure patterns related to memorizing the originals. We show that this happens even if the models are otherwise able to solve problems with different descriptions but requiring the same logic. Our results highlight that out-of-distribution generalization is still problematic for frontier language models and the new generation of thinking models, even for simple reasoning tasks, and making tasks easier does not necessarily imply improved performance.

Mind the Graph When Balancing Data for Fairness or Robustness

Failures of fairness or robustness in machine learning predictive settings can be due to undesired dependencies between covariates, outcomes and auxiliary factors of variation. A common strategy to mitigate these failures is data balancing, which attempts to remove those undesired dependencies. In this work, we define conditions on the training distribution for data balancing to lead to fair or robust models. Our results display that, in many cases, the balanced distribution does not correspond to selectively removing the undesired dependencies in a causal graph of the task, leading to multiple failure modes and even interference with other mitigation techniques such as regularization. Overall, our results highlight the importance of taking the causal graph into account before performing data balancing.

Additive Causal Bandits with Unknown Graph

We explore algorithms to select actions in the causal bandit setting where the learner can choose to intervene on a set of random variables related by a causal graph, and the learner sequentially chooses interventions and observes a sample from the interventional distribution. The learner's goal is to quickly find the intervention, among all interventions on observable variables, that maximizes the expectation of an outcome variable. We depart from previous literature by assuming no knowledge of the causal graph except that latent confounders between the outcome and its ancestors are not present. We first show that the unknown graph problem can be exponentially hard in the parents of the outcome. To remedy this, we adopt an additional additive assumption on the outcome which allows us to solve the problem by casting it as an additive combinatorial linear bandit problem with full-bandit feedback. We propose a novel action-elimination algorithm for this setting, show how to apply this algorithm to the causal bandit problem, provide sample complexity bounds, and empirically validate our findings on a suite of randomly generated causal models, effectively showing that one does not need to explicitly learn the parents of the outcome to identify the best intervention.

Constrained Causal Bayesian Optimization

We propose constrained causal Bayesian optimization (cCBO), an approach for finding interventions in a known causal graph that optimize a target variable under some constraints. cCBO first reduces the search space by exploiting the graph structure and, if available, an observational dataset; and then solves the restricted optimization problem by modelling target and constraint quantities using Gaussian processes and by sequentially selecting interventions via a constrained expected improvement acquisition function. We propose different surrogate models that enable to integrate observational and interventional data while capturing correlation among effects with increasing levels of sophistication. We evaluate cCBO on artificial and real-world causal graphs showing successful trade off between fast convergence and percentage of feasible interventions.

Pragmatic Fairness: Developing Policies with Outcome Disparity Control

We introduce a causal framework for designing optimal policies that satisfy fairness constraints. We take a pragmatic approach asking what we can do with an action space available to us and only with access to historical data. We propose two different fairness constraints: a moderation breaking constraint which aims at blocking moderation paths from the action and sensitive attribute to the outcome, and by that at reducing disparity in outcome levels as much as the provided action space permits; and an equal benefit constraint which aims at distributing gain from the new and maximized policy equally across sensitive attribute levels, and thus at keeping pre-existing preferential treatment in place or avoiding the introduction of new disparity. We introduce practical methods for implementing the constraints and illustrate their uses on experiments with semi-synthetic models.

Prequential MDL for Causal Structure Learning with Neural Networks

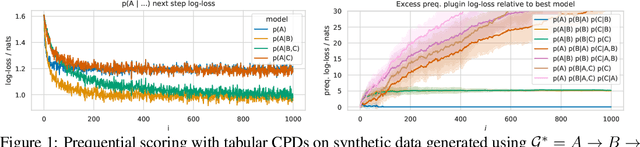
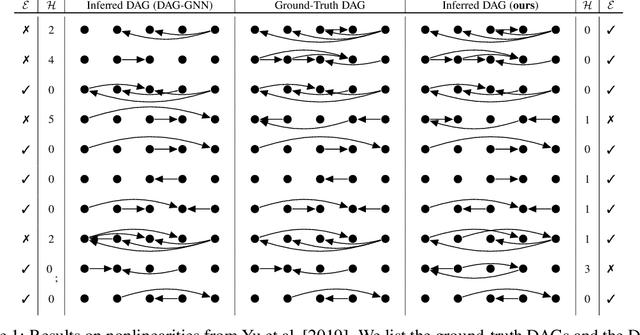
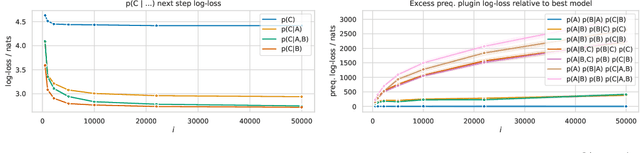
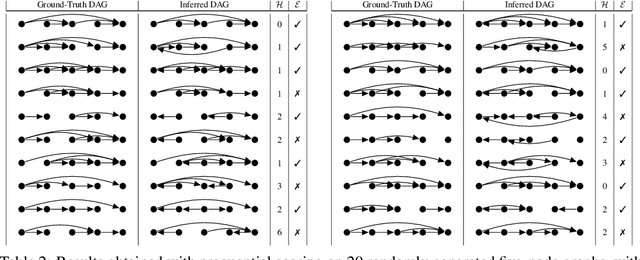
Learning the structure of Bayesian networks and causal relationships from observations is a common goal in several areas of science and technology. We show that the prequential minimum description length principle (MDL) can be used to derive a practical scoring function for Bayesian networks when flexible and overparametrized neural networks are used to model the conditional probability distributions between observed variables. MDL represents an embodiment of Occam's Razor and we obtain plausible and parsimonious graph structures without relying on sparsity inducing priors or other regularizers which must be tuned. Empirically we demonstrate competitive results on synthetic and real-world data. The score often recovers the correct structure even in the presence of strongly nonlinear relationships between variables; a scenario were prior approaches struggle and usually fail. Furthermore we discuss how the the prequential score relates to recent work that infers causal structure from the speed of adaptation when the observations come from a source undergoing distributional shift.

Large-Scale Markov Decision Problems via the Linear Programming Dual

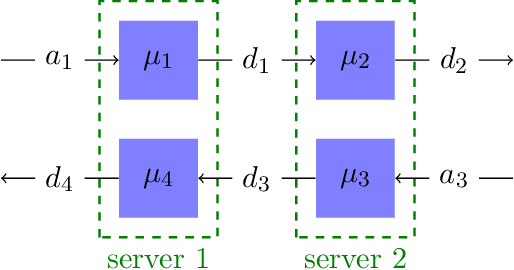
We consider the problem of controlling a fully specified Markov decision process (MDP), also known as the planning problem, when the state space is very large and calculating the optimal policy is intractable. Instead, we pursue the more modest goal of optimizing over some small family of policies. Specifically, we show that the family of policies associated with a low-dimensional approximation of occupancy measures yields a tractable optimization. Moreover, we propose an efficient algorithm, scaling with the size of the subspace but not the state space, that is able to find a policy with low excess loss relative to the best policy in this class. To the best of our knowledge, such results did not exist in the literature previously. We bound excess loss in the average cost and discounted cost cases, which are treated separately. Preliminary experiments show the effectiveness of the proposed algorithms in a queueing application.

Best Arm Identification for Contaminated Bandits

This paper studies active learning in the context of robust statistics. Specifically, we propose a variant of the Best Arm Identification problem for \emph{contaminated bandits}, where each arm pull has probability $\varepsilon$ of generating a sample from an arbitrary contamination distribution instead of the true underlying distribution. The goal is to identify the best (or approximately best) true distribution with high probability, with a secondary goal of providing guarantees on the quality of this distribution. The primary challenge of the contaminated bandit setting is that the true distributions are only partially identifiable, even with infinite samples. To address this, we first develop tight, non-asymptotic sample complexity bounds for high-probability estimation of the first two robust moments (median and median absolute deviation) from contaminated samples, which may be of independent interest. Using these results, we adapt several classical Best Arm Identification algorithms to the contaminated bandit setting and derive sample complexity upper bounds for our problem. Finally, we provide matching information-theoretic lower bounds on the sample complexity (up to a small logarithmic factor). Our results suggest an inherent robustness of classical Best Arm Identification algorithms.

Hit-and-Run for Sampling and Planning in Non-Convex Spaces

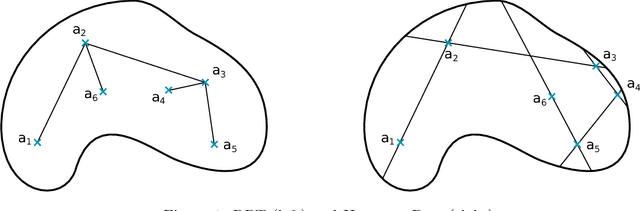
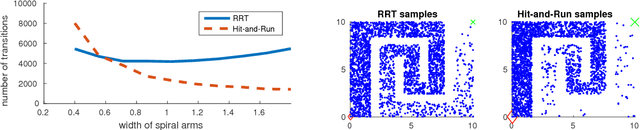
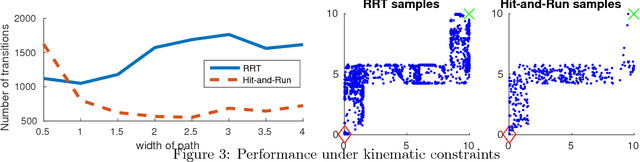
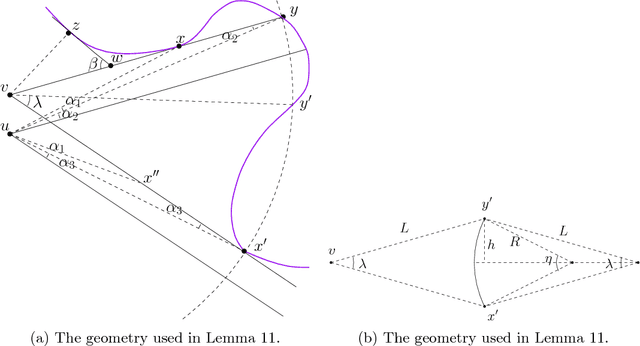
We propose the Hit-and-Run algorithm for planning and sampling problems in non-convex spaces. For sampling, we show the first analysis of the Hit-and-Run algorithm in non-convex spaces and show that it mixes fast as long as certain smoothness conditions are satisfied. In particular, our analysis reveals an intriguing connection between fast mixing and the existence of smooth measure-preserving mappings from a convex space to the non-convex space. For planning, we show advantages of Hit-and-Run compared to state-of-the-art planning methods such as Rapidly-Exploring Random Trees.

Online Isotonic Regression

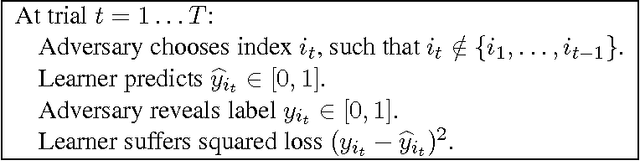
We consider the online version of the isotonic regression problem. Given a set of linearly ordered points (e.g., on the real line), the learner must predict labels sequentially at adversarially chosen positions and is evaluated by her total squared loss compared against the best isotonic (non-decreasing) function in hindsight. We survey several standard online learning algorithms and show that none of them achieve the optimal regret exponent; in fact, most of them (including Online Gradient Descent, Follow the Leader and Exponential Weights) incur linear regret. We then prove that the Exponential Weights algorithm played over a covering net of isotonic functions has a regret bounded by $O\big(T^{1/3} \log^{2/3}(T)\big)$ and present a matching $\Omega(T^{1/3})$ lower bound on regret. We provide a computationally efficient version of this algorithm. We also analyze the noise-free case, in which the revealed labels are isotonic, and show that the bound can be improved to $O(\log T)$ or even to $O(1)$ (when the labels are revealed in isotonic order). Finally, we extend the analysis beyond squared loss and give bounds for entropic loss and absolute loss.