Hit-and-Run for Sampling and Planning in Non-Convex Spaces
Paper and Code
Oct 19, 2016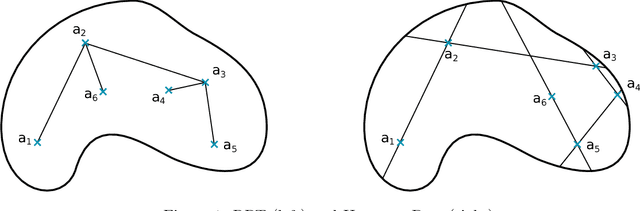
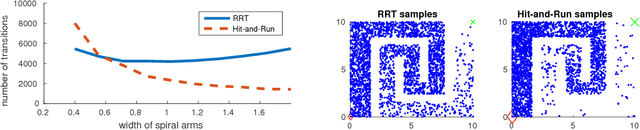
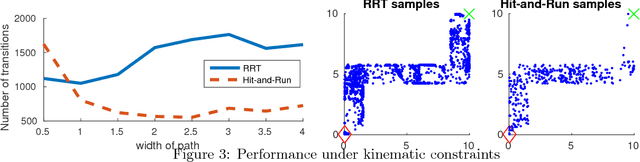
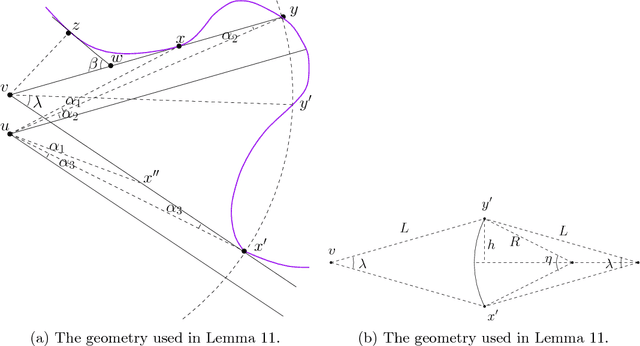
We propose the Hit-and-Run algorithm for planning and sampling problems in non-convex spaces. For sampling, we show the first analysis of the Hit-and-Run algorithm in non-convex spaces and show that it mixes fast as long as certain smoothness conditions are satisfied. In particular, our analysis reveals an intriguing connection between fast mixing and the existence of smooth measure-preserving mappings from a convex space to the non-convex space. For planning, we show advantages of Hit-and-Run compared to state-of-the-art planning methods such as Rapidly-Exploring Random Trees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge