Functional Causal Bayesian Optimization
Paper and Code
Jun 10, 2023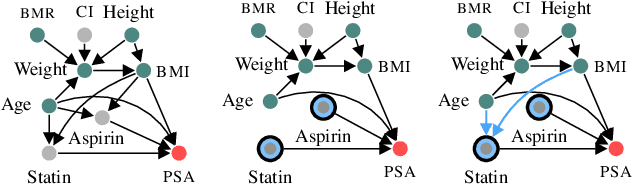

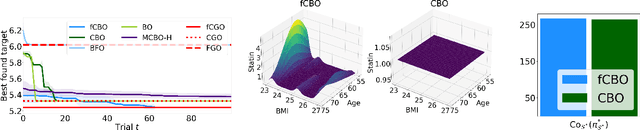
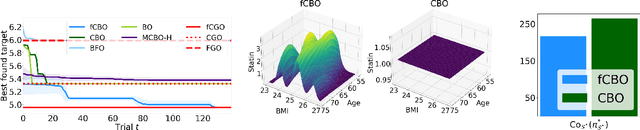
We propose functional causal Bayesian optimization (fCBO), a method for finding interventions that optimize a target variable in a known causal graph. fCBO extends the CBO family of methods to enable functional interventions, which set a variable to be a deterministic function of other variables in the graph. fCBO models the unknown objectives with Gaussian processes whose inputs are defined in a reproducing kernel Hilbert space, thus allowing to compute distances among vector-valued functions. In turn, this enables to sequentially select functions to explore by maximizing an expected improvement acquisition functional while keeping the typical computational tractability of standard BO settings. We introduce graphical criteria that establish when considering functional interventions allows attaining better target effects, and conditions under which selected interventions are also optimal for conditional target effects. We demonstrate the benefits of the method in a synthetic and in a real-world causal graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge