Danilo Jimenez Rezende
Can foundation models actively gather information in interactive environments to test hypotheses?
Dec 09, 2024



Abstract:While problem solving is a standard evaluation task for foundation models, a crucial component of problem solving -- actively and strategically gathering information to test hypotheses -- has not been closely investigated. To assess the information gathering abilities of foundation models in interactive environments, we introduce a framework in which a model must determine the factors influencing a hidden reward function by iteratively reasoning about its previously gathered information and proposing its next exploratory action to maximize information gain at each step. We implement this framework in both a text-based environment, which offers a tightly controlled setting and enables high-throughput parameter sweeps, and in an embodied 3D environment, which requires addressing complexities of multi-modal interaction more relevant to real-world applications. We further investigate whether approaches such as self-correction and increased inference time improve information gathering efficiency. In a relatively simple task that requires identifying a single rewarding feature, we find that LLM's information gathering capability is close to optimal. However, when the model must identify a conjunction of rewarding features, performance is suboptimal. The hit in performance is due partly to the model translating task description to a policy and partly to the model's effectiveness in using its in-context memory. Performance is comparable in both text and 3D embodied environments, although imperfect visual object recognition reduces its accuracy in drawing conclusions from gathered information in the 3D embodied case. For single-feature-based rewards, we find that smaller models curiously perform better; for conjunction-based rewards, incorporating self correction into the model improves performance.
Learning to Induce Causal Structure
Apr 11, 2022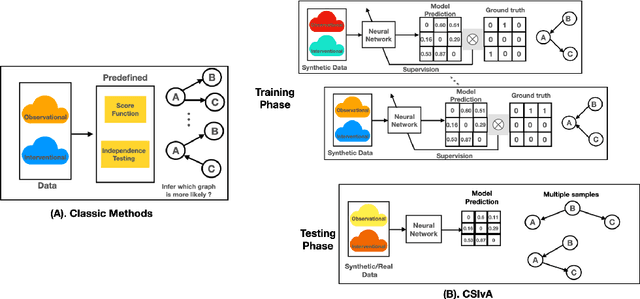
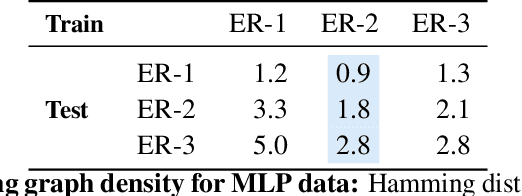
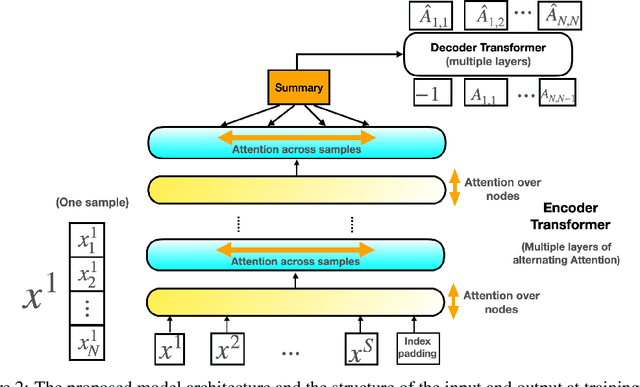
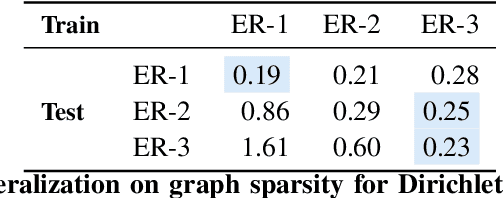
Abstract:The fundamental challenge in causal induction is to infer the underlying graph structure given observational and/or interventional data. Most existing causal induction algorithms operate by generating candidate graphs and then evaluating them using either score-based methods (including continuous optimization) or independence tests. In this work, instead of proposing scoring function or independence tests, we treat the inference process as a black box and design a neural network architecture that learns the mapping from both observational and interventional data to graph structures via supervised training on synthetic graphs. We show that the proposed model generalizes not only to new synthetic graphs but also to naturalistic graphs.
Introduction to Normalizing Flows for Lattice Field Theory
Jan 20, 2021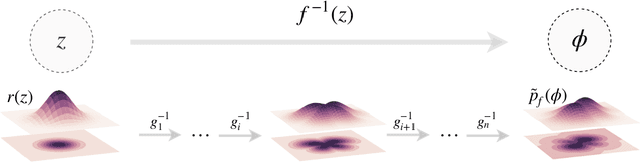

Abstract:This notebook tutorial demonstrates a method for sampling Boltzmann distributions of lattice field theories using a class of machine learning models known as normalizing flows. The ideas and approaches proposed in arXiv:1904.12072, arXiv:2002.02428, and arXiv:2003.06413 are reviewed and a concrete implementation of the framework is presented. We apply this framework to a lattice scalar field theory and to U(1) gauge theory, explicitly encoding gauge symmetries in the flow-based approach to the latter. This presentation is intended to be interactive and working with the attached Jupyter notebook is recommended.
Sampling using $SU(N)$ gauge equivariant flows
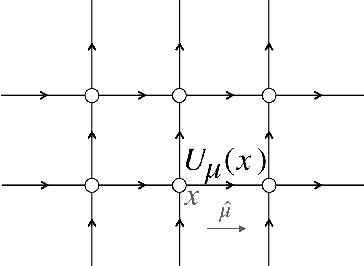
Aug 12, 2020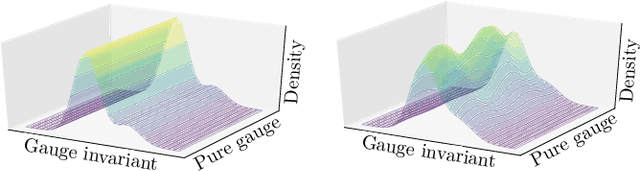

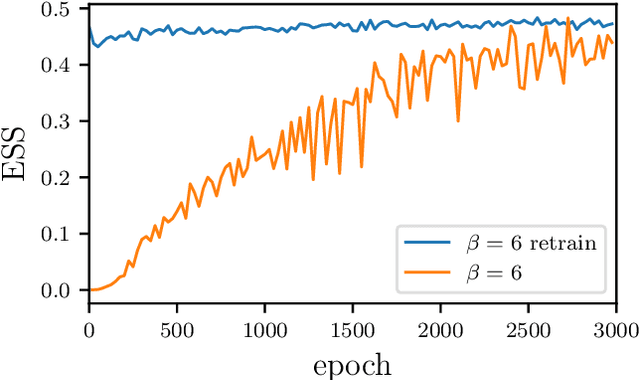
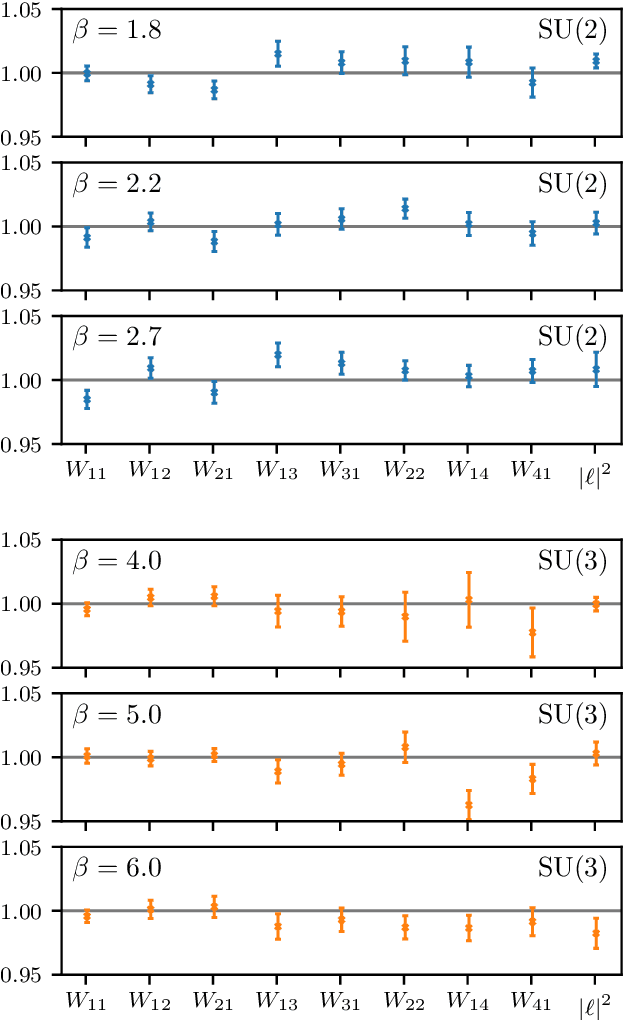
Abstract:We develop a flow-based sampling algorithm for $SU(N)$ lattice gauge theories that is gauge-invariant by construction. Our key contribution is constructing a class of flows on an $SU(N)$ variable (or on a $U(N)$ variable by a simple alternative) that respect matrix conjugation symmetry. We apply this technique to sample distributions of single $SU(N)$ variables and to construct flow-based samplers for $SU(2)$ and $SU(3)$ lattice gauge theory in two dimensions.
Neural Communication Systems with Bandwidth-limited Channel
Apr 01, 2020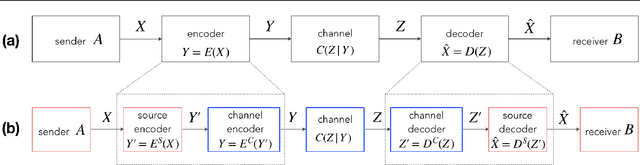
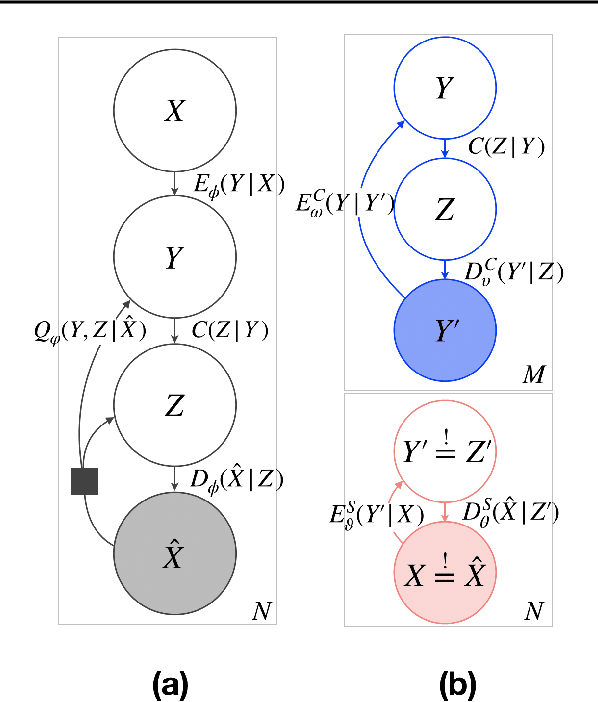
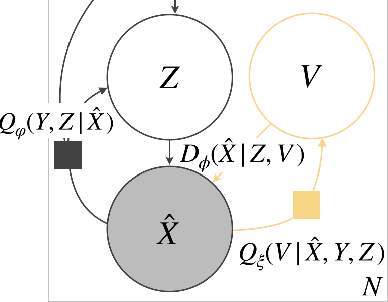
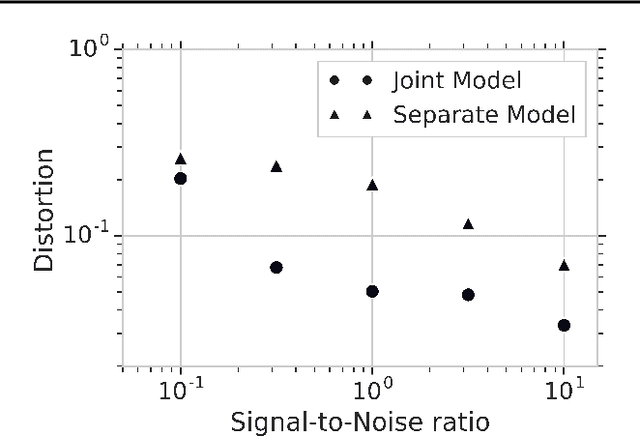
Abstract:Reliably transmitting messages despite information loss due to a noisy channel is a core problem of information theory. One of the most important aspects of real world communication, e.g. via wifi, is that it may happen at varying levels of information transfer. The bandwidth-limited channel models this phenomenon. In this study we consider learning coding with the bandwidth-limited channel (BWLC). Recently, neural communication models such as variational autoencoders have been studied for the task of source compression. We build upon this work by studying neural communication systems with the BWLC. Specifically,we find three modelling choices that are relevant under expected information loss. First, instead of separating the sub-tasks of compression (source coding) and error correction (channel coding), we propose to model both jointly. Framing the problem as a variational learning problem, we conclude that joint systems outperform their separate counterparts when coding is performed by flexible learnable function approximators such as neural networks. To facilitate learning, we introduce a differentiable and computationally efficient version of the bandwidth-limited channel. Second, we propose a design to model missing information with a prior, and incorporate this into the channel model. Finally, sampling from the joint model is improved by introducing auxiliary latent variables in the decoder. Experimental results justify the validity of our design decisions through improved distortion and FID scores.
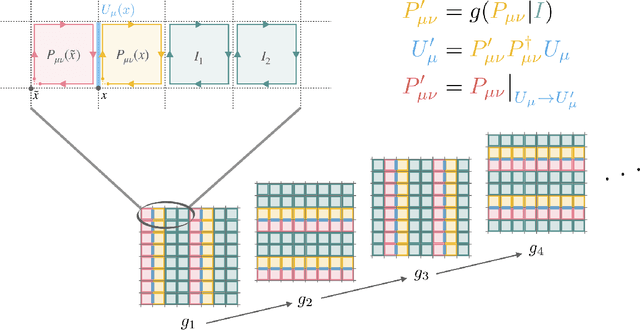
Equivariant flow-based sampling for lattice gauge theory
Mar 13, 2020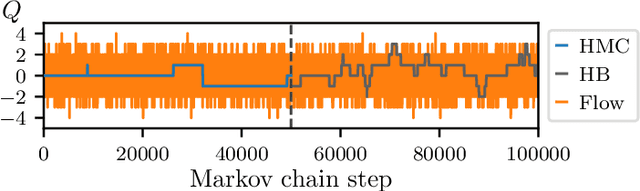

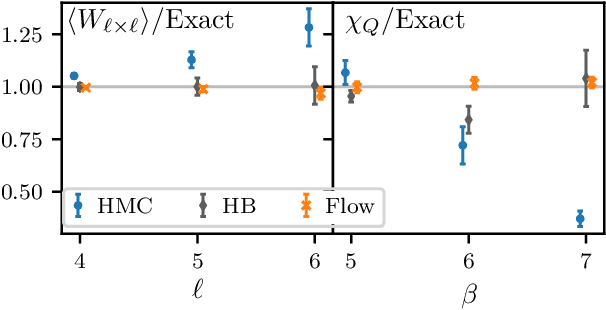
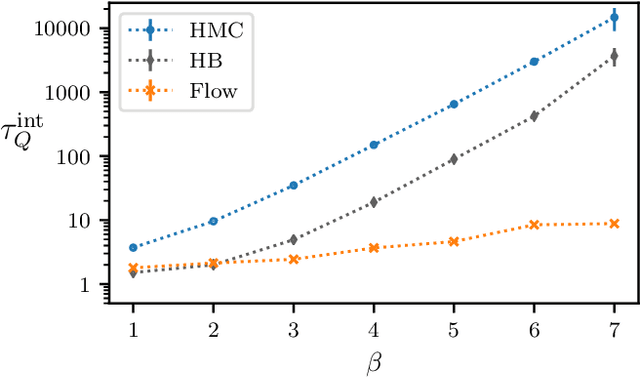
Abstract:We define a class of machine-learned flow-based sampling algorithms for lattice gauge theories that are gauge-invariant by construction. We demonstrate the application of this framework to U(1) gauge theory in two spacetime dimensions, and find that near critical points in parameter space the approach is orders of magnitude more efficient at sampling topological quantities than more traditional sampling procedures such as Hybrid Monte Carlo and Heat Bath.
Targeted free energy estimation via learned mappings
Feb 12, 2020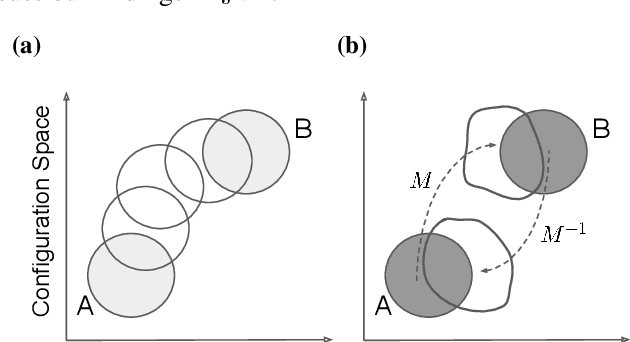
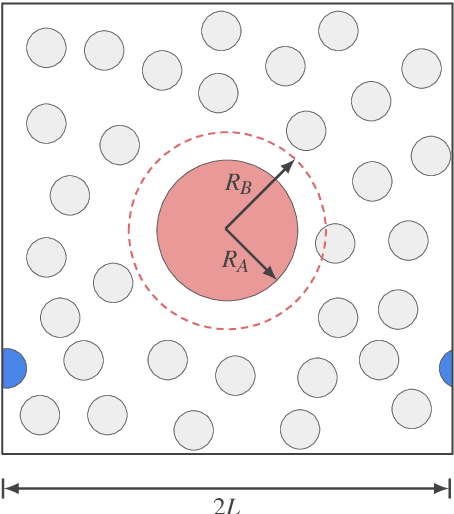
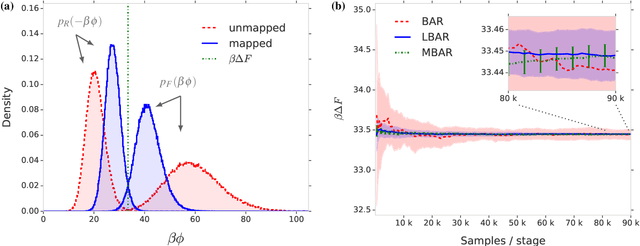
Abstract:Free energy perturbation (FEP) was proposed by Zwanzig more than six decades ago as a method to estimate free energy differences, and has since inspired a huge body of related methods that use it as an integral building block. Being an importance sampling based estimator, however, FEP suffers from a severe limitation: the requirement of sufficient overlap between distributions. One strategy to mitigate this problem, called Targeted Free Energy Perturbation, uses a high-dimensional mapping in configuration space to increase overlap of the underlying distributions. Despite its potential, this method has attracted only limited attention due to the formidable challenge of formulating a tractable mapping. Here, we cast Targeted FEP as a machine learning (ML) problem in which the mapping is parameterized as a neural network that is optimized so as to increase overlap. We test our method on a fully-periodic solvation system, with a model that respects the inherent permutational and periodic symmetries of the problem. We demonstrate that our method leads to a substantial variance reduction in free energy estimates when compared against baselines.
Normalizing Flows on Tori and Spheres
Feb 06, 2020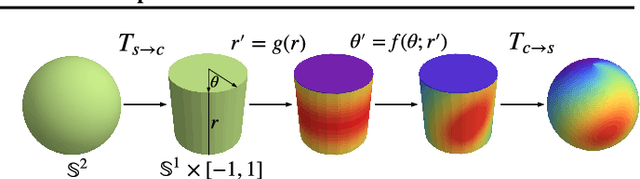


Abstract:Normalizing flows are a powerful tool for building expressive distributions in high dimensions. So far, most of the literature has concentrated on learning flows on Euclidean spaces. Some problems however, such as those involving angles, are defined on spaces with more complex geometries, such as tori or spheres. In this paper, we propose and compare expressive and numerically stable flows on such spaces. Our flows are built recursively on the dimension of the space, starting from flows on circles, closed intervals or spheres.
Normalizing Flows for Probabilistic Modeling and Inference
Dec 05, 2019
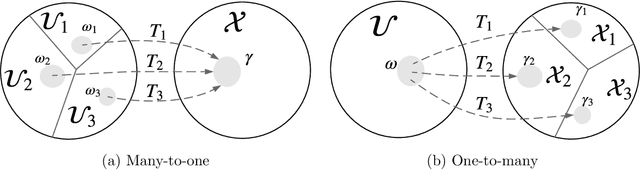
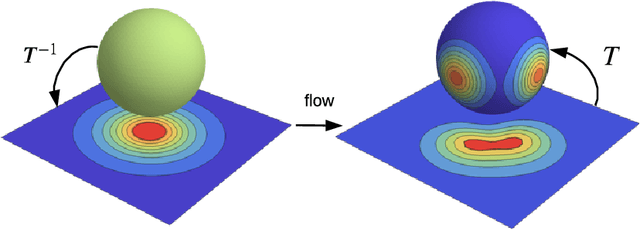
Abstract:Normalizing flows provide a general mechanism for defining expressive probability distributions, only requiring the specification of a (usually simple) base distribution and a series of bijective transformations. There has been much recent work on normalizing flows, ranging from improving their expressive power to expanding their application. We believe the field has now matured and is in need of a unified perspective. In this review, we attempt to provide such a perspective by describing flows through the lens of probabilistic modeling and inference. We place special emphasis on the fundamental principles of flow design, and discuss foundational topics such as expressive power and computational trade-offs. We also broaden the conceptual framing of flows by relating them to more general probability transformations. Lastly, we summarize the use of flows for tasks such as generative modeling, approximate inference, and supervised learning.
Information bottleneck through variational glasses
Dec 05, 2019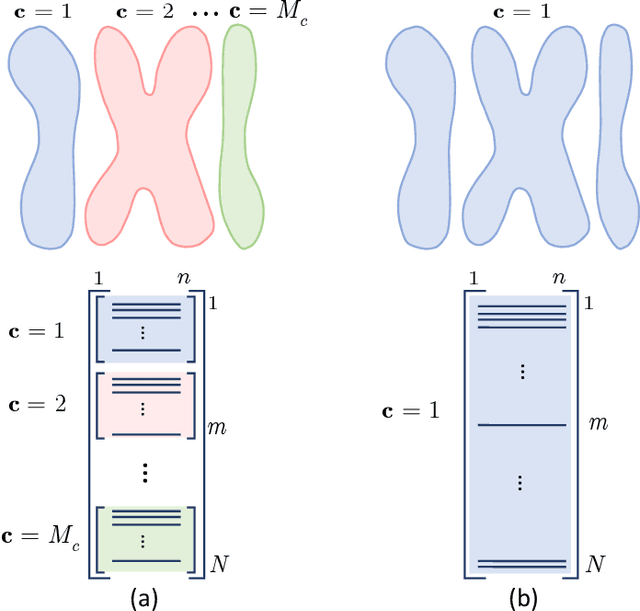
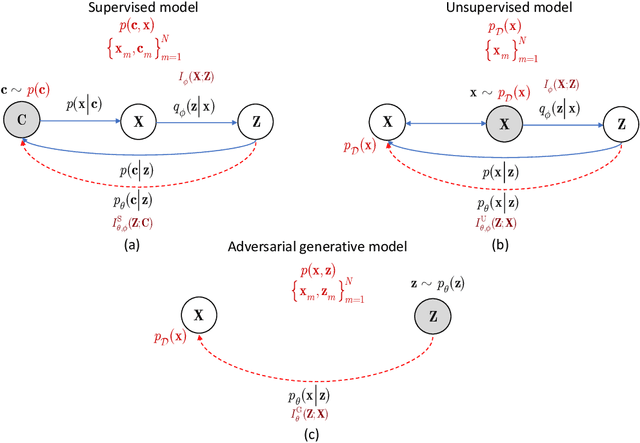
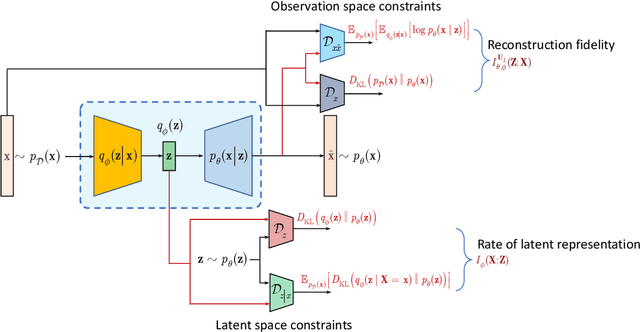
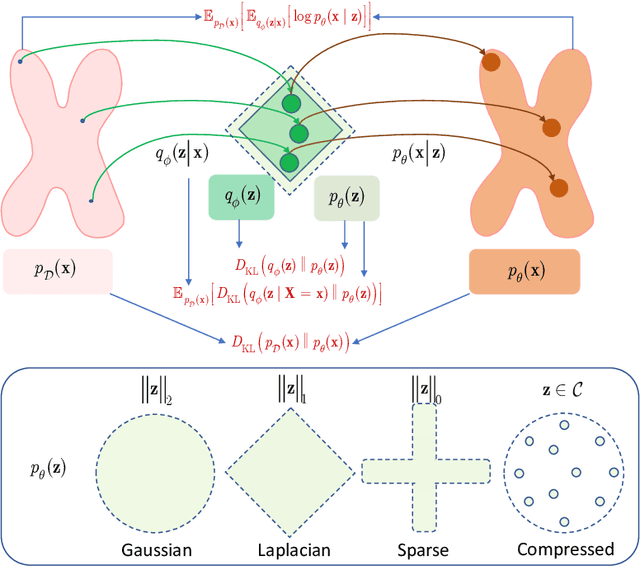
Abstract:Information bottleneck (IB) principle [1] has become an important element in information-theoretic analysis of deep models. Many state-of-the-art generative models of both Variational Autoencoder (VAE) [2; 3] and Generative Adversarial Networks (GAN) [4] families use various bounds on mutual information terms to introduce certain regularization constraints [5; 6; 7; 8; 9; 10]. Accordingly, the main difference between these models consists in add regularization constraints and targeted objectives. In this work, we will consider the IB framework for three classes of models that include supervised, unsupervised and adversarial generative models. We will apply a variational decomposition leading a common structure and allowing easily establish connections between these models and analyze underlying assumptions. Based on these results, we focus our analysis on unsupervised setup and reconsider the VAE family. In particular, we present a new interpretation of VAE family based on the IB framework using a direct decomposition of mutual information terms and show some interesting connections to existing methods such as VAE [2; 3], beta-VAE [11], AAE [12], InfoVAE [5] and VAE/GAN [13]. Instead of adding regularization constraints to an evidence lower bound (ELBO) [2; 3], which itself is a lower bound, we show that many known methods can be considered as a product of variational decomposition of mutual information terms in the IB framework. The proposed decomposition might also contribute to the interpretability of generative models of both VAE and GAN families and create a new insights to a generative compression [14; 15; 16; 17]. It can also be of interest for the analysis of novelty detection based on one-class classifiers [18] with the IB based discriminators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge