Target Score Matching

Denoising Score Matching estimates the score of a noised version of a target distribution by minimizing a regression loss and is widely used to train the popular class of Denoising Diffusion Models. A well known limitation of Denoising Score Matching, however, is that it yields poor estimates of the score at low noise levels. This issue is particularly unfavourable for problems in the physical sciences and for Monte Carlo sampling tasks for which the score of the clean original target is known. Intuitively, estimating the score of a slightly noised version of the target should be a simple task in such cases. In this paper, we address this shortcoming and show that it is indeed possible to leverage knowledge of the target score. We present a Target Score Identity and corresponding Target Score Matching regression loss which allows us to obtain score estimates admitting favourable properties at low noise levels.

Gibbs free energies via isobaric-isothermal flows

We present a machine-learning model based on normalizing flows that is trained to sample from the isobaric-isothermal (NPT) ensemble. In our approach, we approximate the joint distribution of a fully-flexible triclinic simulation box and particle coordinates to achieve a desired internal pressure. We test our model on monatomic water in the cubic and hexagonal ice phases and find excellent agreement of Gibbs free energies and other observables compared with established baselines.

GraphCast: Learning skillful medium-range global weather forecasting

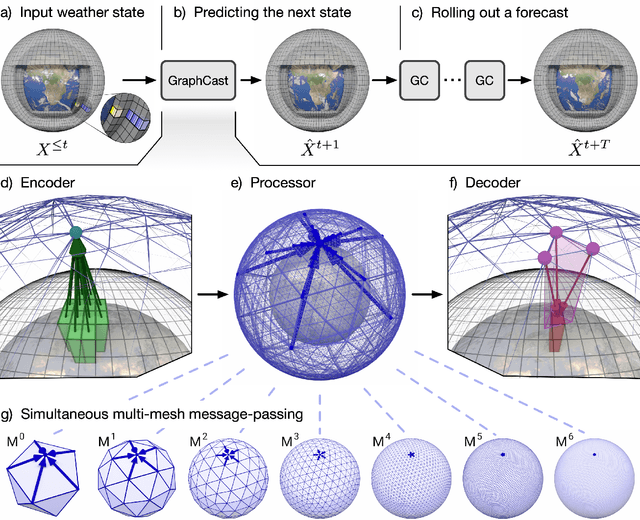
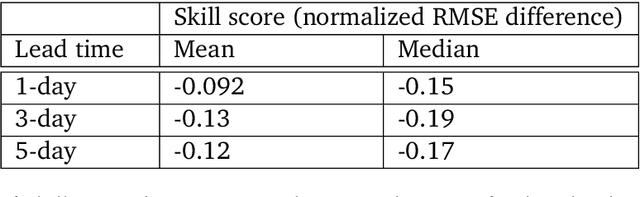
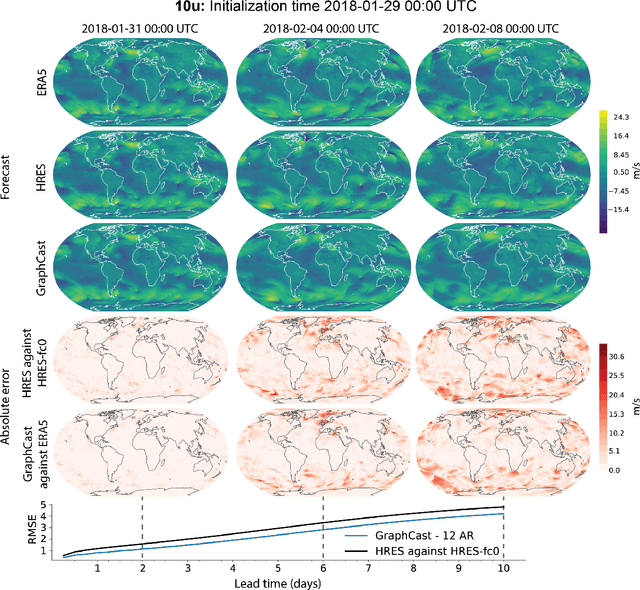
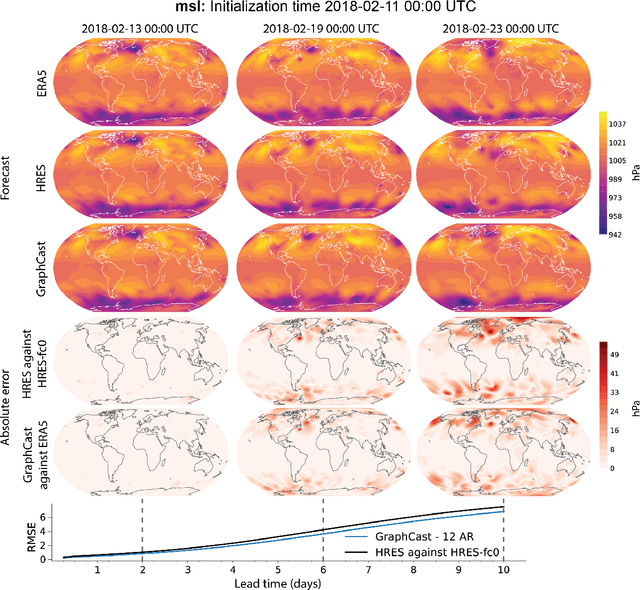
We introduce a machine-learning (ML)-based weather simulator--called "GraphCast"--which outperforms the most accurate deterministic operational medium-range weather forecasting system in the world, as well as all previous ML baselines. GraphCast is an autoregressive model, based on graph neural networks and a novel high-resolution multi-scale mesh representation, which we trained on historical weather data from the European Centre for Medium-Range Weather Forecasts (ECMWF)'s ERA5 reanalysis archive. It can make 10-day forecasts, at 6-hour time intervals, of five surface variables and six atmospheric variables, each at 37 vertical pressure levels, on a 0.25-degree latitude-longitude grid, which corresponds to roughly 25 x 25 kilometer resolution at the equator. Our results show GraphCast is more accurate than ECMWF's deterministic operational forecasting system, HRES, on 90.0% of the 2760 variable and lead time combinations we evaluated. GraphCast also outperforms the most accurate previous ML-based weather forecasting model on 99.2% of the 252 targets it reported. GraphCast can generate a 10-day forecast (35 gigabytes of data) in under 60 seconds on Cloud TPU v4 hardware. Unlike traditional forecasting methods, ML-based forecasting scales well with data: by training on bigger, higher quality, and more recent data, the skill of the forecasts can improve. Together these results represent a key step forward in complementing and improving weather modeling with ML, open new opportunities for fast, accurate forecasting, and help realize the promise of ML-based simulation in the physical sciences.

MultiScale MeshGraphNets

In recent years, there has been a growing interest in using machine learning to overcome the high cost of numerical simulation, with some learned models achieving impressive speed-ups over classical solvers whilst maintaining accuracy. However, these methods are usually tested at low-resolution settings, and it remains to be seen whether they can scale to the costly high-resolution simulations that we ultimately want to tackle. In this work, we propose two complementary approaches to improve the framework from MeshGraphNets, which demonstrated accurate predictions in a broad range of physical systems. MeshGraphNets relies on a message passing graph neural network to propagate information, and this structure becomes a limiting factor for high-resolution simulations, as equally distant points in space become further apart in graph space. First, we demonstrate that it is possible to learn accurate surrogate dynamics of a high-resolution system on a much coarser mesh, both removing the message passing bottleneck and improving performance; and second, we introduce a hierarchical approach (MultiScale MeshGraphNets) which passes messages on two different resolutions (fine and coarse), significantly improving the accuracy of MeshGraphNets while requiring less computational resources.

Normalizing flows for atomic solids

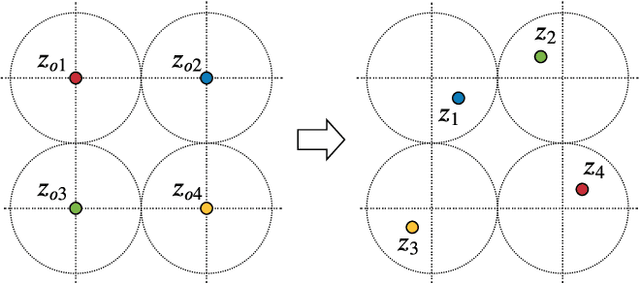
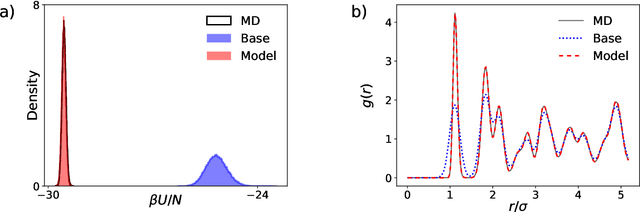
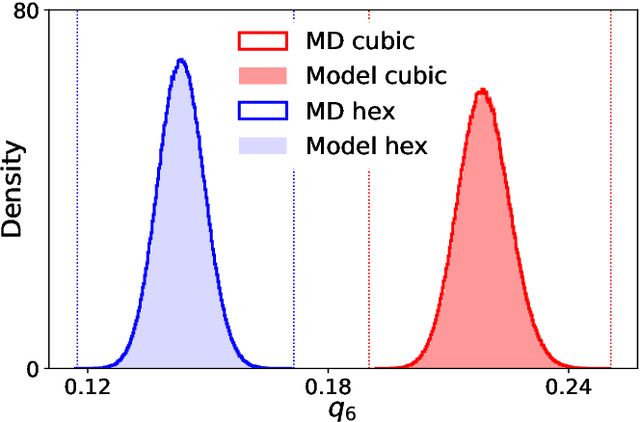
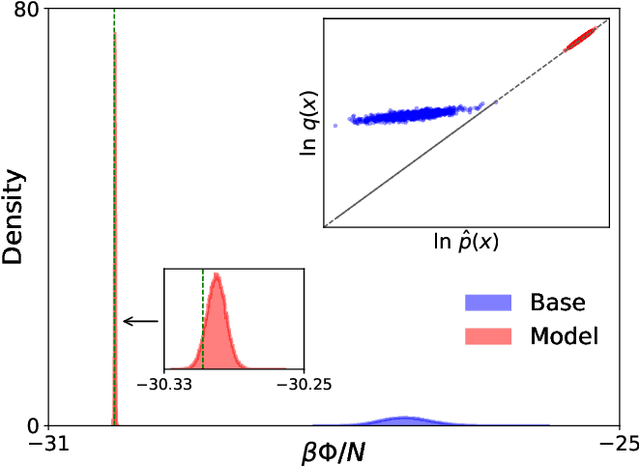
We present a machine-learning approach, based on normalizing flows, for modelling atomic solids. Our model transforms an analytically tractable base distribution into the target solid without requiring ground-truth samples for training. We report Helmholtz free energy estimates for cubic and hexagonal ice modelled as monatomic water as well as for a truncated and shifted Lennard-Jones system, and find them to be in excellent agreement with literature values and with estimates from established baseline methods. We further investigate structural properties and show that the model samples are nearly indistinguishable from the ones obtained with molecular dynamics. Our results thus demonstrate that normalizing flows can provide high-quality samples and free energy estimates of solids, without the need for multi-staging or for imposing restrictions on the crystal geometry.

SyMetric: Measuring the Quality of Learnt Hamiltonian Dynamics Inferred from Vision

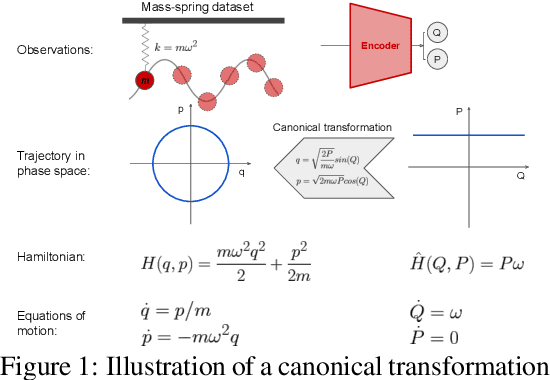
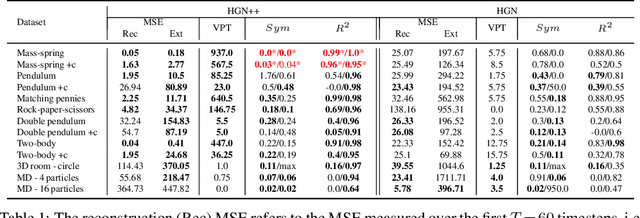
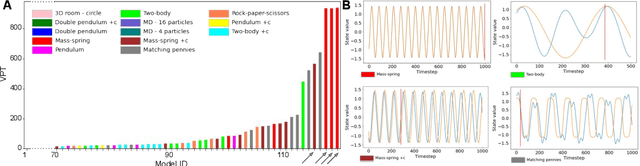
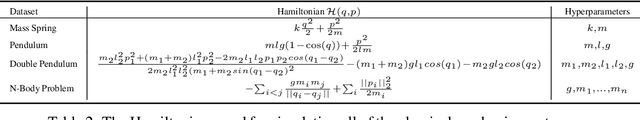
A recently proposed class of models attempts to learn latent dynamics from high-dimensional observations, like images, using priors informed by Hamiltonian mechanics. While these models have important potential applications in areas like robotics or autonomous driving, there is currently no good way to evaluate their performance: existing methods primarily rely on image reconstruction quality, which does not always reflect the quality of the learnt latent dynamics. In this work, we empirically highlight the problems with the existing measures and develop a set of new measures, including a binary indicator of whether the underlying Hamiltonian dynamics have been faithfully captured, which we call Symplecticity Metric or SyMetric. Our measures take advantage of the known properties of Hamiltonian dynamics and are more discriminative of the model's ability to capture the underlying dynamics than reconstruction error. Using SyMetric, we identify a set of architectural choices that significantly improve the performance of a previously proposed model for inferring latent dynamics from pixels, the Hamiltonian Generative Network (HGN). Unlike the original HGN, the new HGN++ is able to discover an interpretable phase space with physically meaningful latents on some datasets. Furthermore, it is stable for significantly longer rollouts on a diverse range of 13 datasets, producing rollouts of essentially infinite length both forward and backwards in time with no degradation in quality on a subset of the datasets.

Which priors matter? Benchmarking models for learning latent dynamics

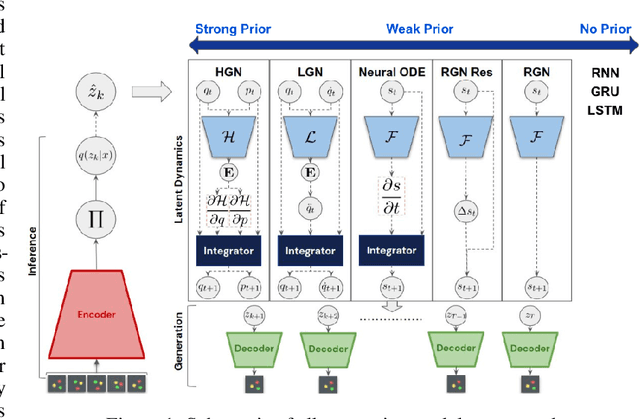
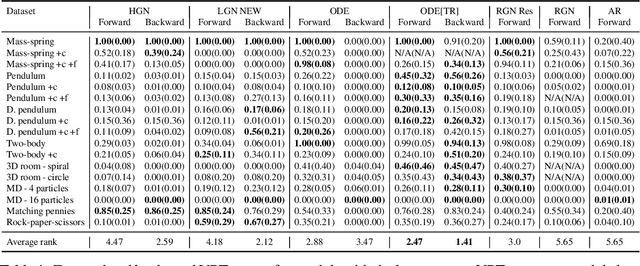
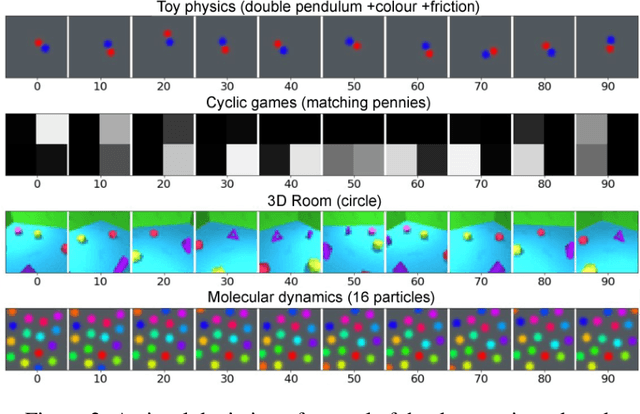
Learning dynamics is at the heart of many important applications of machine learning (ML), such as robotics and autonomous driving. In these settings, ML algorithms typically need to reason about a physical system using high dimensional observations, such as images, without access to the underlying state. Recently, several methods have proposed to integrate priors from classical mechanics into ML models to address the challenge of physical reasoning from images. In this work, we take a sober look at the current capabilities of these models. To this end, we introduce a suite consisting of 17 datasets with visual observations based on physical systems exhibiting a wide range of dynamics. We conduct a thorough and detailed comparison of the major classes of physically inspired methods alongside several strong baselines. While models that incorporate physical priors can often learn latent spaces with desirable properties, our results demonstrate that these methods fail to significantly improve upon standard techniques. Nonetheless, we find that the use of continuous and time-reversible dynamics benefits models of all classes.

Targeted free energy estimation via learned mappings

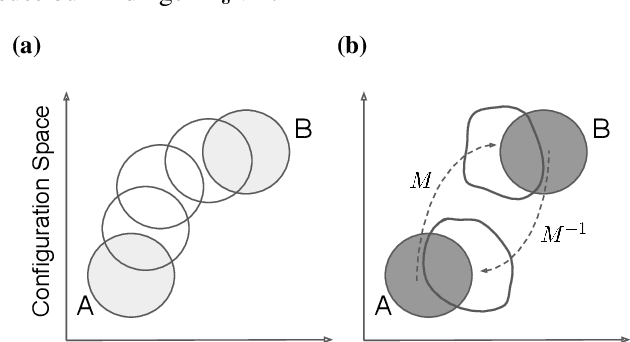
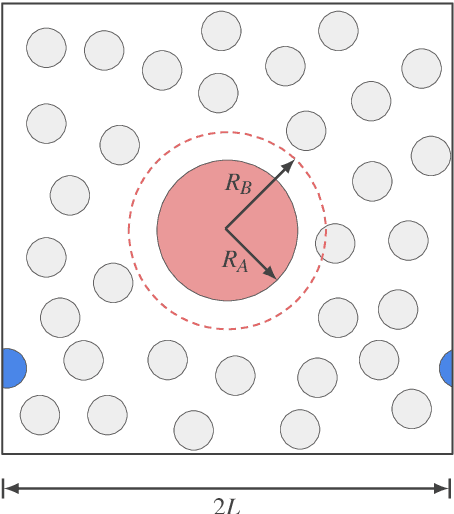
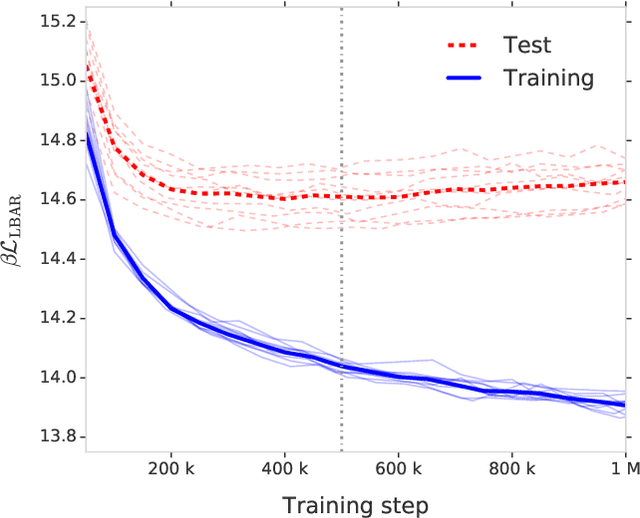
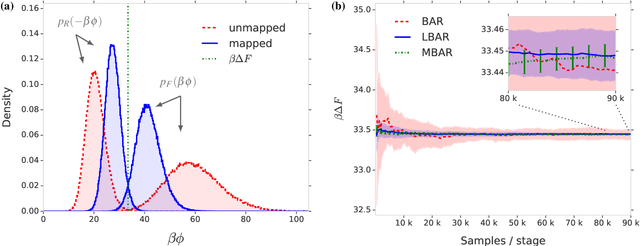
Free energy perturbation (FEP) was proposed by Zwanzig more than six decades ago as a method to estimate free energy differences, and has since inspired a huge body of related methods that use it as an integral building block. Being an importance sampling based estimator, however, FEP suffers from a severe limitation: the requirement of sufficient overlap between distributions. One strategy to mitigate this problem, called Targeted Free Energy Perturbation, uses a high-dimensional mapping in configuration space to increase overlap of the underlying distributions. Despite its potential, this method has attracted only limited attention due to the formidable challenge of formulating a tractable mapping. Here, we cast Targeted FEP as a machine learning (ML) problem in which the mapping is parameterized as a neural network that is optimized so as to increase overlap. We test our method on a fully-periodic solvation system, with a model that respects the inherent permutational and periodic symmetries of the problem. We demonstrate that our method leads to a substantial variance reduction in free energy estimates when compared against baselines.