Andrew J. Ballard
Normalizing flows for atomic solids
Nov 16, 2021
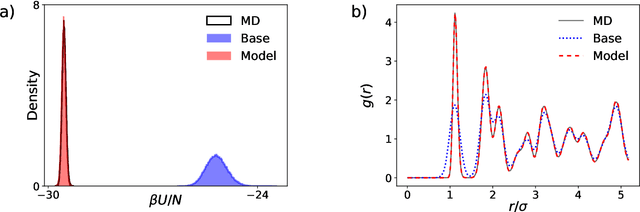
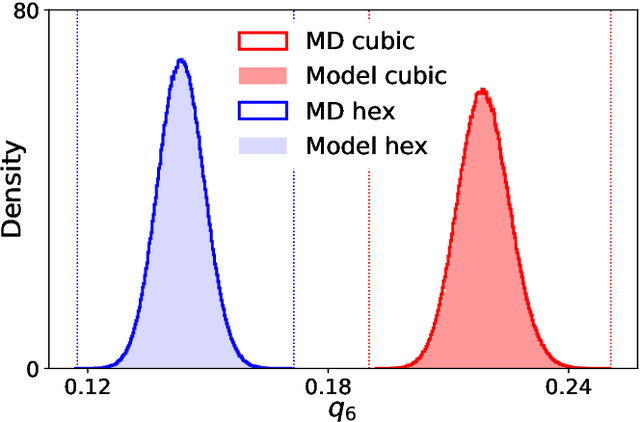
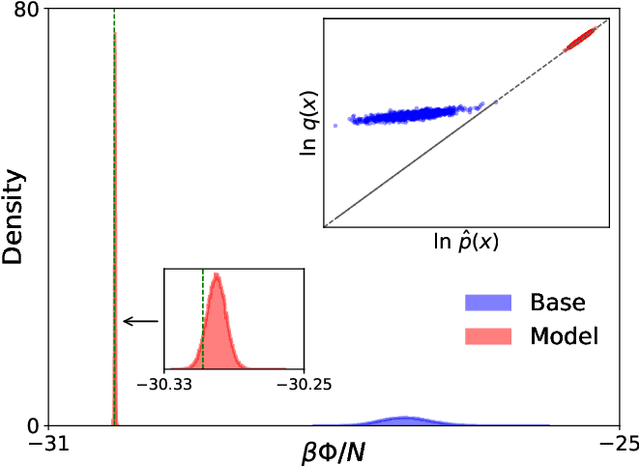
Abstract:We present a machine-learning approach, based on normalizing flows, for modelling atomic solids. Our model transforms an analytically tractable base distribution into the target solid without requiring ground-truth samples for training. We report Helmholtz free energy estimates for cubic and hexagonal ice modelled as monatomic water as well as for a truncated and shifted Lennard-Jones system, and find them to be in excellent agreement with literature values and with estimates from established baseline methods. We further investigate structural properties and show that the model samples are nearly indistinguishable from the ones obtained with molecular dynamics. Our results thus demonstrate that normalizing flows can provide high-quality samples and free energy estimates of solids, without the need for multi-staging or for imposing restrictions on the crystal geometry.
Targeted free energy estimation via learned mappings
Feb 12, 2020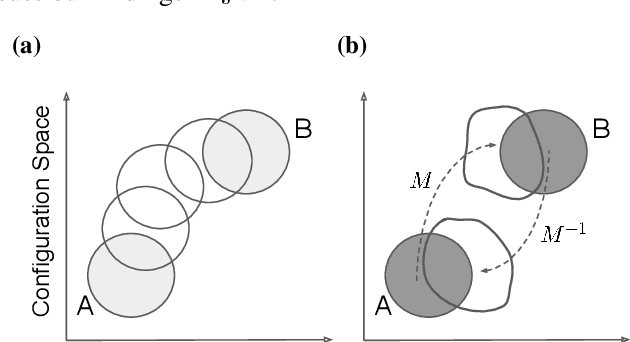
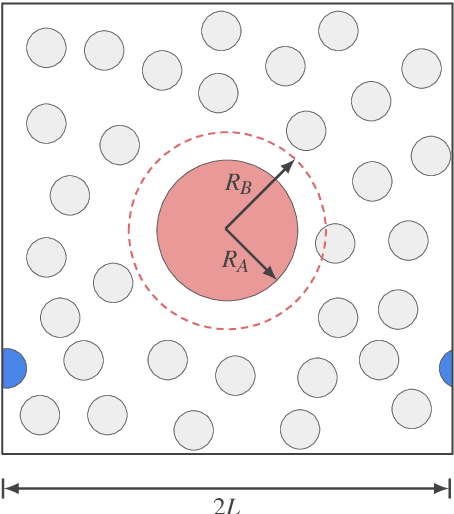
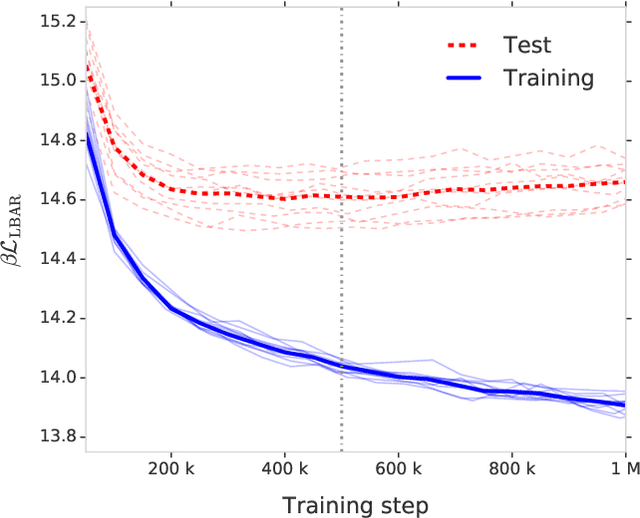
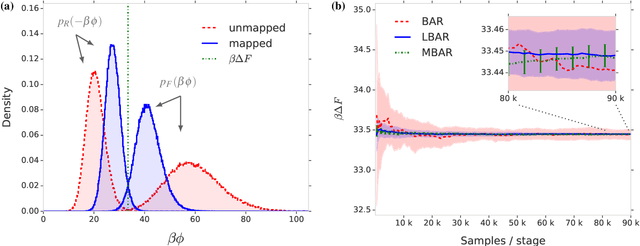
Abstract:Free energy perturbation (FEP) was proposed by Zwanzig more than six decades ago as a method to estimate free energy differences, and has since inspired a huge body of related methods that use it as an integral building block. Being an importance sampling based estimator, however, FEP suffers from a severe limitation: the requirement of sufficient overlap between distributions. One strategy to mitigate this problem, called Targeted Free Energy Perturbation, uses a high-dimensional mapping in configuration space to increase overlap of the underlying distributions. Despite its potential, this method has attracted only limited attention due to the formidable challenge of formulating a tractable mapping. Here, we cast Targeted FEP as a machine learning (ML) problem in which the mapping is parameterized as a neural network that is optimized so as to increase overlap. We test our method on a fully-periodic solvation system, with a model that respects the inherent permutational and periodic symmetries of the problem. We demonstrate that our method leads to a substantial variance reduction in free energy estimates when compared against baselines.
Metacontrol for Adaptive Imagination-Based Optimization
May 07, 2017



Abstract:Many machine learning systems are built to solve the hardest examples of a particular task, which often makes them large and expensive to run---especially with respect to the easier examples, which might require much less computation. For an agent with a limited computational budget, this "one-size-fits-all" approach may result in the agent wasting valuable computation on easy examples, while not spending enough on hard examples. Rather than learning a single, fixed policy for solving all instances of a task, we introduce a metacontroller which learns to optimize a sequence of "imagined" internal simulations over predictive models of the world in order to construct a more informed, and more economical, solution. The metacontroller component is a model-free reinforcement learning agent, which decides both how many iterations of the optimization procedure to run, as well as which model to consult on each iteration. The models (which we call "experts") can be state transition models, action-value functions, or any other mechanism that provides information useful for solving the task, and can be learned on-policy or off-policy in parallel with the metacontroller. When the metacontroller, controller, and experts were trained with "interaction networks" (Battaglia et al., 2016) as expert models, our approach was able to solve a challenging decision-making problem under complex non-linear dynamics. The metacontroller learned to adapt the amount of computation it performed to the difficulty of the task, and learned how to choose which experts to consult by factoring in both their reliability and individual computational resource costs. This allowed the metacontroller to achieve a lower overall cost (task loss plus computational cost) than more traditional fixed policy approaches. These results demonstrate that our approach is a powerful framework for using...
Perspective: Energy Landscapes for Machine Learning
Mar 23, 2017



Abstract:Machine learning techniques are being increasingly used as flexible non-linear fitting and prediction tools in the physical sciences. Fitting functions that exhibit multiple solutions as local minima can be analysed in terms of the corresponding machine learning landscape. Methods to explore and visualise molecular potential energy landscapes can be applied to these machine learning landscapes to gain new insight into the solution space involved in training and the nature of the corresponding predictions. In particular, we can define quantities analogous to molecular structure, thermodynamics, and kinetics, and relate these emergent properties to the structure of the underlying landscape. This Perspective aims to describe these analogies with examples from recent applications, and suggest avenues for new interdisciplinary research.
Learning to Navigate in Complex Environments
Jan 13, 2017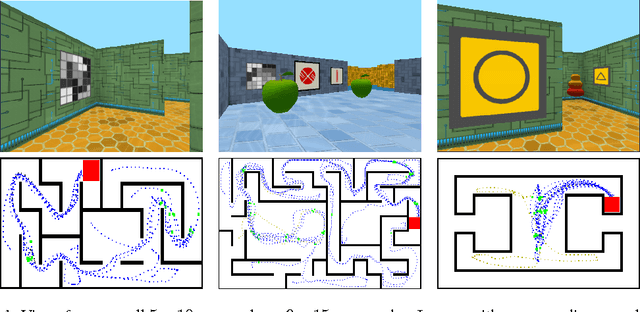
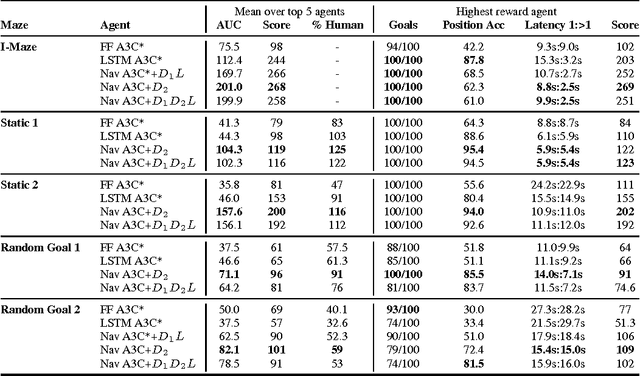
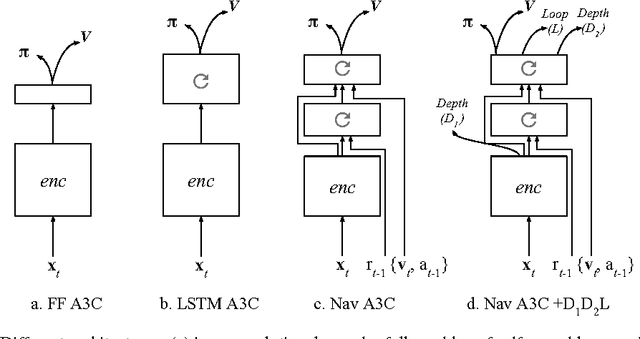
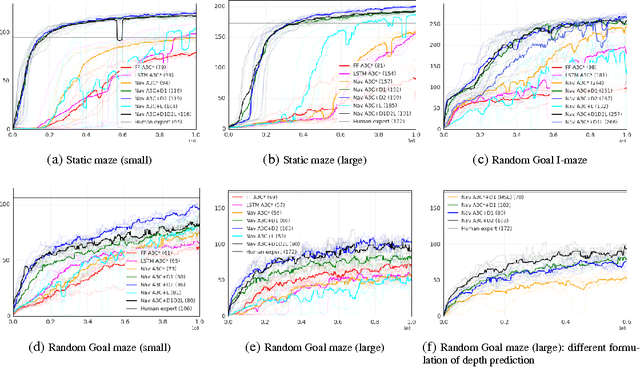
Abstract:Learning to navigate in complex environments with dynamic elements is an important milestone in developing AI agents. In this work we formulate the navigation question as a reinforcement learning problem and show that data efficiency and task performance can be dramatically improved by relying on additional auxiliary tasks leveraging multimodal sensory inputs. In particular we consider jointly learning the goal-driven reinforcement learning problem with auxiliary depth prediction and loop closure classification tasks. This approach can learn to navigate from raw sensory input in complicated 3D mazes, approaching human-level performance even under conditions where the goal location changes frequently. We provide detailed analysis of the agent behaviour, its ability to localise, and its network activity dynamics, showing that the agent implicitly learns key navigation abilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge