David J. Wales
Evolution of $K$-means solution landscapes with the addition of dataset outliers and a robust clustering comparison measure for their analysis
Jun 25, 2023Abstract:The $K$-means algorithm remains one of the most widely-used clustering methods due to its simplicity and general utility. The performance of $K$-means depends upon location of minima low in cost function, amongst a potentially vast number of solutions. Here, we use the energy landscape approach to map the change in $K$-means solution space as a result of increasing dataset outliers and show that the cost function surface becomes more funnelled. Kinetic analysis reveals that in all cases the overall funnel is composed of shallow locally-funnelled regions, each of which are separated by areas that do not support any clustering solutions. These shallow regions correspond to different types of clustering solution and their increasing number with outliers leads to longer pathways within the funnel and a reduced correlation between accuracy and cost function. Finally, we propose that the rates obtained from kinetic analysis provide a novel measure of clustering similarity that incorporates information about the paths between them. This measure is robust to outliers and we illustrate the application to datasets containing multiple outliers.
Physics Inspired Approaches Towards Understanding Gaussian Processes
May 18, 2023Abstract:Prior beliefs about the latent function to shape inductive biases can be incorporated into a Gaussian Process (GP) via the kernel. However, beyond kernel choices, the decision-making process of GP models remains poorly understood. In this work, we contribute an analysis of the loss landscape for GP models using methods from physics. We demonstrate $\nu$-continuity for Matern kernels and outline aspects of catastrophe theory at critical points in the loss landscape. By directly including $\nu$ in the hyperparameter optimisation for Matern kernels, we find that typical values of $\nu$ are far from optimal in terms of performance, yet prevail in the literature due to the increased computational speed. We also provide an a priori method for evaluating the effect of GP ensembles and discuss various voting approaches based on physical properties of the loss landscape. The utility of these approaches is demonstrated for various synthetic and real datasets. Our findings provide an enhanced understanding of the decision-making process behind GPs and offer practical guidance for improving their performance and interpretability in a range of applications.
The Loss Surface of XOR Artificial Neural Networks
Apr 06, 2018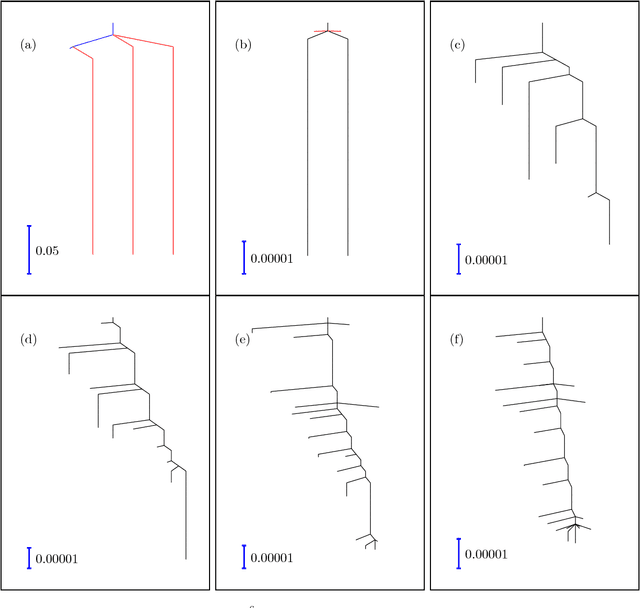
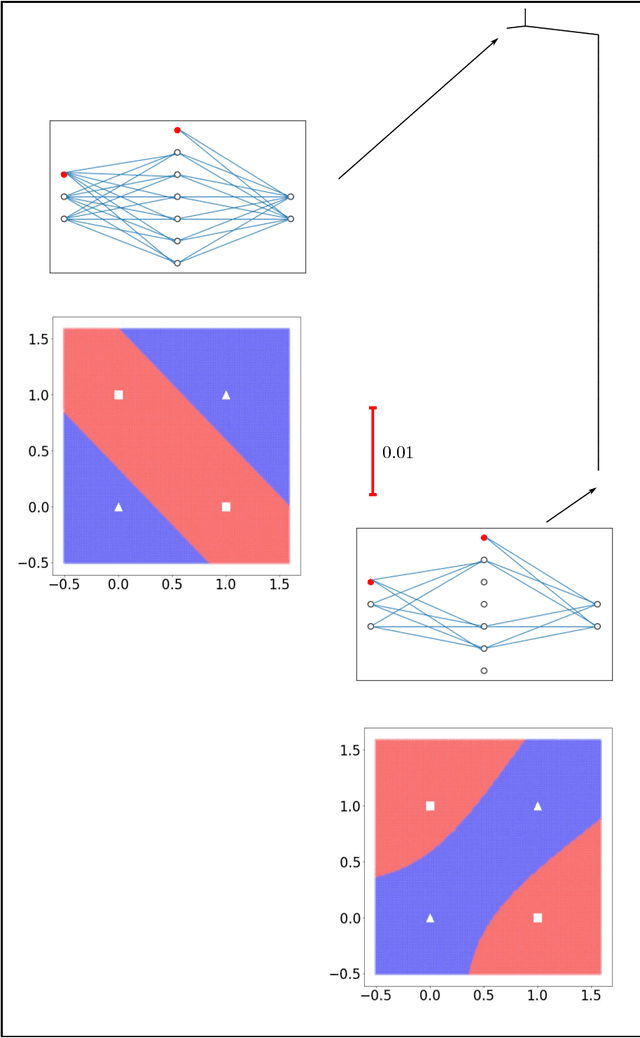
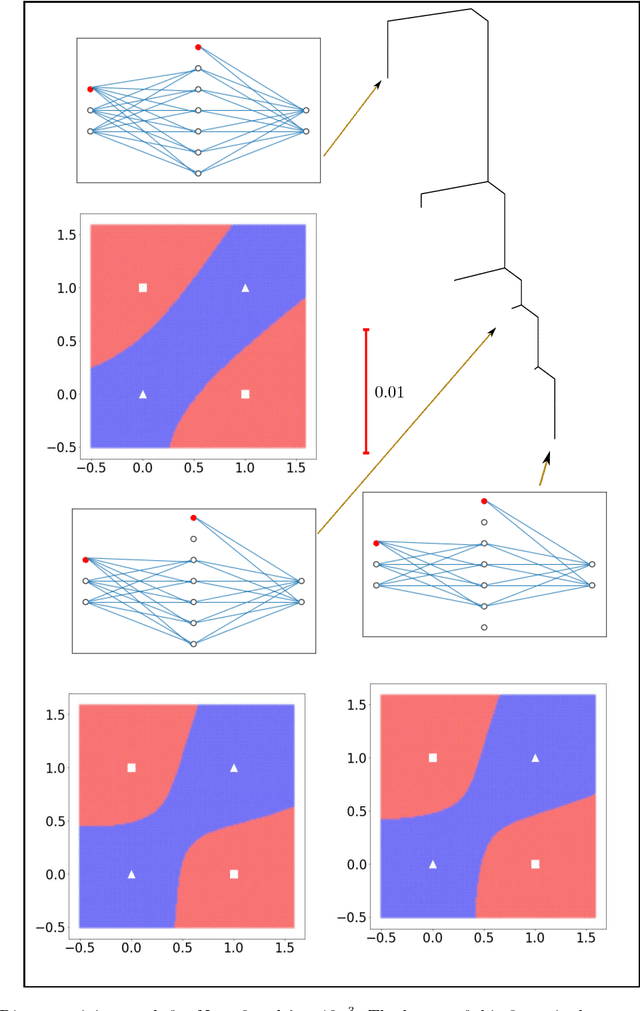
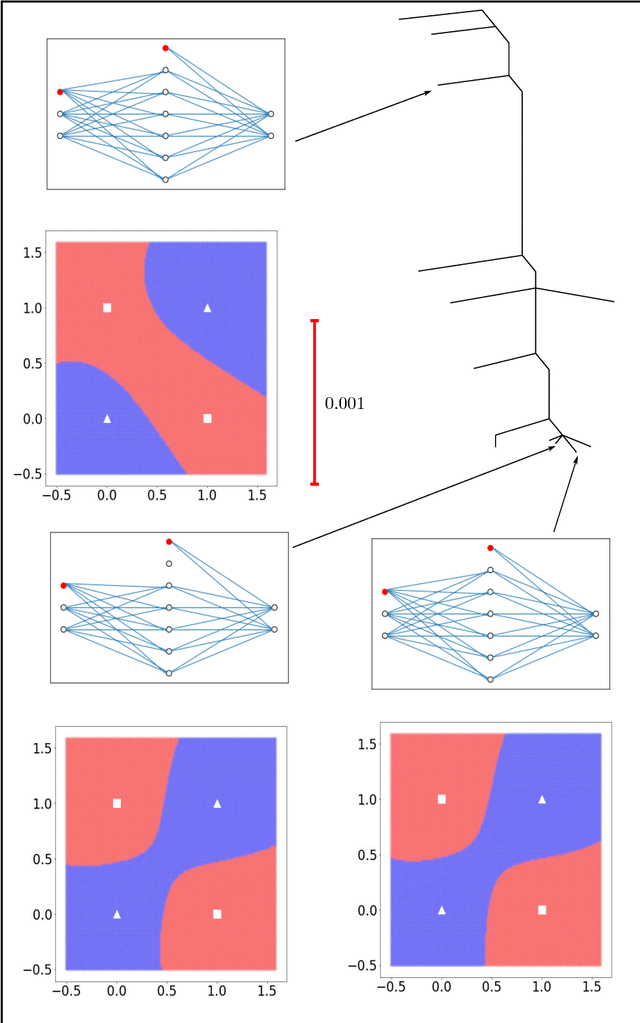
Abstract:Training an artificial neural network involves an optimization process over the landscape defined by the cost (loss) as a function of the network parameters. We explore these landscapes using optimisation tools developed for potential energy landscapes in molecular science. The number of local minima and transition states (saddle points of index one), as well as the ratio of transition states to minima, grow rapidly with the number of nodes in the network. There is also a strong dependence on the regularisation parameter, with the landscape becoming more convex (fewer minima) as the regularisation term increases. We demonstrate that in our formulation, stationary points for networks with $N_h$ hidden nodes, including the minimal network required to fit the XOR data, are also stationary points for networks with $N_{h} +1$ hidden nodes when all the weights involving the additional nodes are zero. Hence, smaller networks optimized to train the XOR data are embedded in the landscapes of larger networks. Our results clarify certain aspects of the classification and sensitivity (to perturbations in the input data) of minima and saddle points for this system, and may provide insight into dropout and network compression.
* 19 pages, 6 figures. Submitted to journal in Oct, 2017
Perspective: Energy Landscapes for Machine Learning
Mar 23, 2017



Abstract:Machine learning techniques are being increasingly used as flexible non-linear fitting and prediction tools in the physical sciences. Fitting functions that exhibit multiple solutions as local minima can be analysed in terms of the corresponding machine learning landscape. Methods to explore and visualise molecular potential energy landscapes can be applied to these machine learning landscapes to gain new insight into the solution space involved in training and the nature of the corresponding predictions. In particular, we can define quantities analogous to molecular structure, thermodynamics, and kinetics, and relate these emergent properties to the structure of the underlying landscape. This Perspective aims to describe these analogies with examples from recent applications, and suggest avenues for new interdisciplinary research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge