Towards Robust Deep Neural Networks

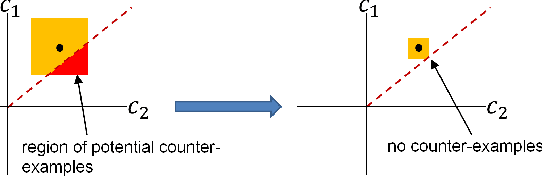
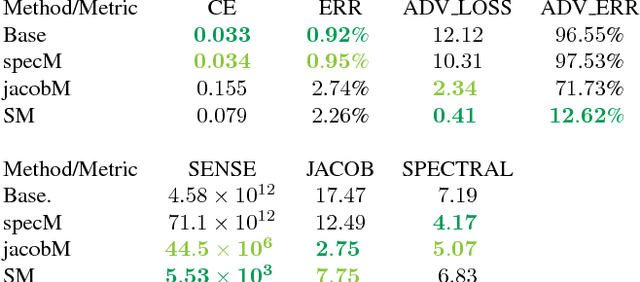
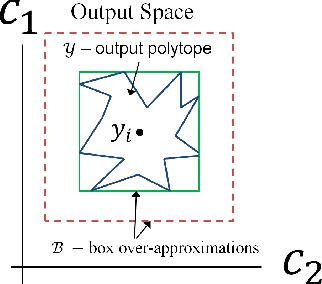
We examine the relationship between the energy landscape of neural networks and their robustness to adversarial attacks. Combining energy landscape techniques developed in computational chemistry with tools drawn from formal methods, we produce empirical evidence that networks corresponding to lower-lying minima in the landscape tend to be more robust. The robustness measure used is the inverse of the sensitivity measure, which we define as the volume of an over-approximation of the reachable set of network outputs under all additive $l_{\infty}$ bounded perturbations on the input data. We present a novel loss function which contains a weighted sensitivity component in addition to the traditional task-oriented and regularization terms. In our experiments on standard machine learning and computer vision datasets (e.g., Iris and MNIST), we show that the proposed loss function leads to networks which reliably optimize the robustness measure as well as other related metrics of adversarial robustness without significant degradation in the classification error.

The Loss Surface of XOR Artificial Neural Networks

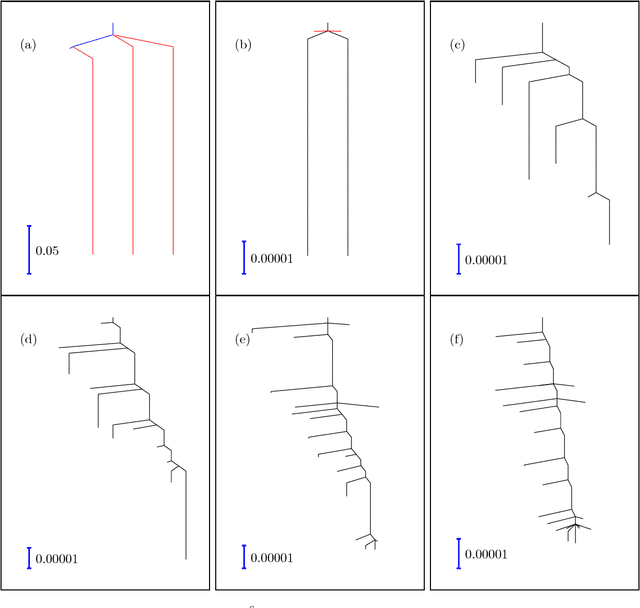
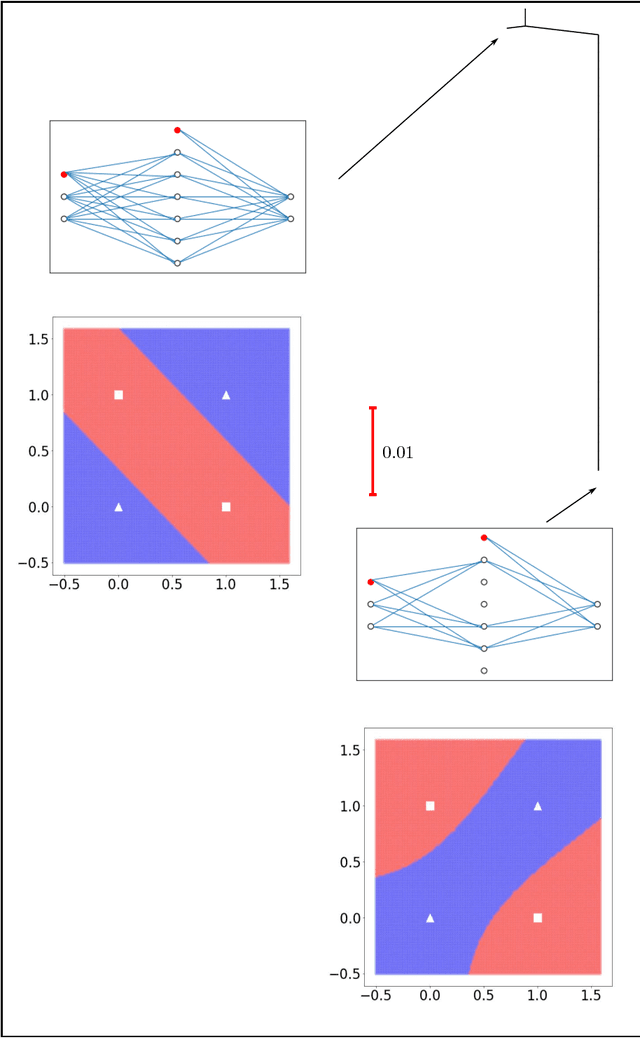
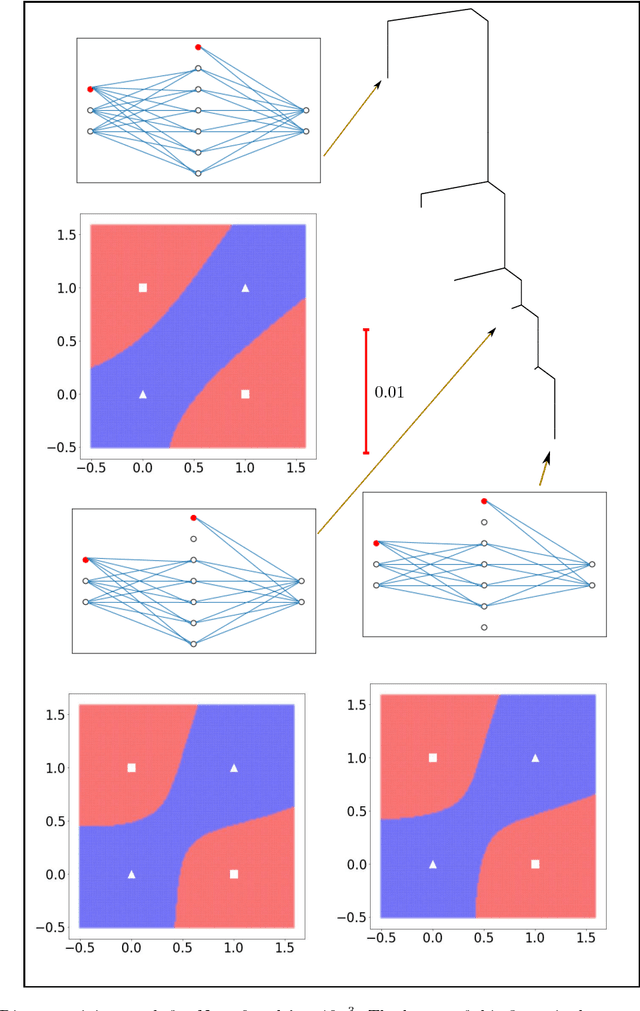
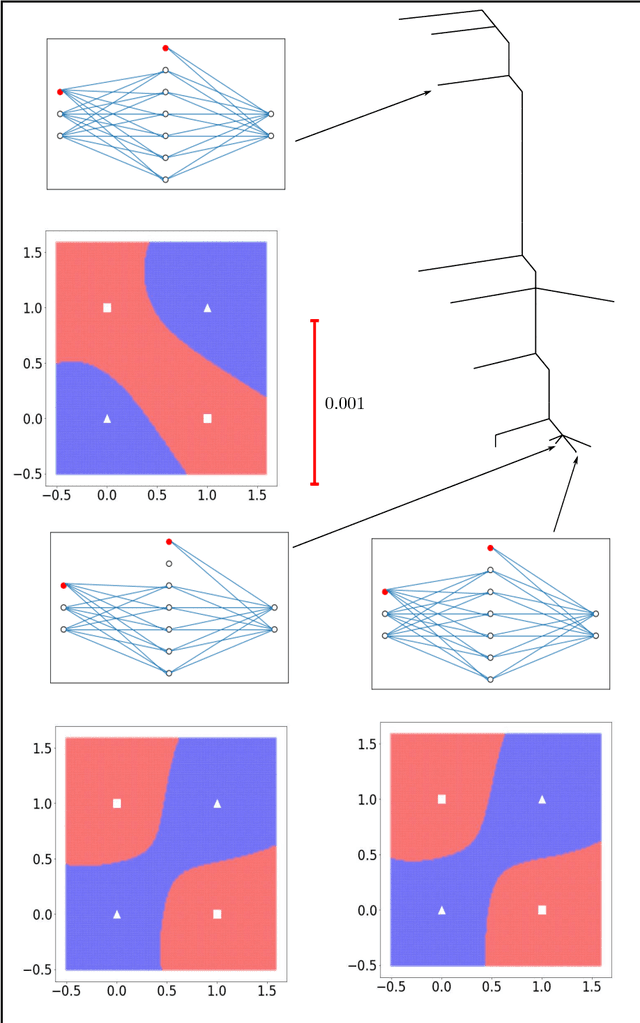
Training an artificial neural network involves an optimization process over the landscape defined by the cost (loss) as a function of the network parameters. We explore these landscapes using optimisation tools developed for potential energy landscapes in molecular science. The number of local minima and transition states (saddle points of index one), as well as the ratio of transition states to minima, grow rapidly with the number of nodes in the network. There is also a strong dependence on the regularisation parameter, with the landscape becoming more convex (fewer minima) as the regularisation term increases. We demonstrate that in our formulation, stationary points for networks with $N_h$ hidden nodes, including the minimal network required to fit the XOR data, are also stationary points for networks with $N_{h} +1$ hidden nodes when all the weights involving the additional nodes are zero. Hence, smaller networks optimized to train the XOR data are embedded in the landscapes of larger networks. Our results clarify certain aspects of the classification and sensitivity (to perturbations in the input data) of minima and saddle points for this system, and may provide insight into dropout and network compression.