Edgar A. Bernal
Manifold Regularization for Memory-Efficient Training of Deep Neural Networks
May 26, 2023Abstract:One of the prevailing trends in the machine- and deep-learning community is to gravitate towards the use of increasingly larger models in order to keep pushing the state-of-the-art performance envelope. This tendency makes access to the associated technologies more difficult for the average practitioner and runs contrary to the desire to democratize knowledge production in the field. In this paper, we propose a framework for achieving improved memory efficiency in the process of learning traditional neural networks by leveraging inductive-bias-driven network design principles and layer-wise manifold-oriented regularization objectives. Use of the framework results in improved absolute performance and empirical generalization error relative to traditional learning techniques. We provide empirical validation of the framework, including qualitative and quantitative evidence of its effectiveness on two standard image datasets, namely CIFAR-10 and CIFAR-100. The proposed framework can be seamlessly combined with existing network compression methods for further memory savings.
Training Deep Normalizing Flow Models in Highly Incomplete Data Scenarios with Prior Regularization
Apr 03, 2021



Abstract:Deep generative frameworks including GANs and normalizing flow models have proven successful at filling in missing values in partially observed data samples by effectively learning -- either explicitly or implicitly -- complex, high-dimensional statistical distributions. In tasks where the data available for learning is only partially observed, however, their performance decays monotonically as a function of the data missingness rate. In high missing data rate regimes (e.g., 60% and above), it has been observed that state-of-the-art models tend to break down and produce unrealistic and/or semantically inaccurate data. We propose a novel framework to facilitate the learning of data distributions in high paucity scenarios that is inspired by traditional formulations of solutions to ill-posed problems. The proposed framework naturally stems from posing the process of learning from incomplete data as a joint optimization task of the parameters of the model being learned and the missing data values. The method involves enforcing a prior regularization term that seamlessly integrates with objectives used to train explicit and tractable deep generative frameworks such as deep normalizing flow models. We demonstrate via extensive experimental validation that the proposed framework outperforms competing techniques, particularly as the rate of data paucity approaches unity.
Machine learning the real discriminant locus
Jun 24, 2020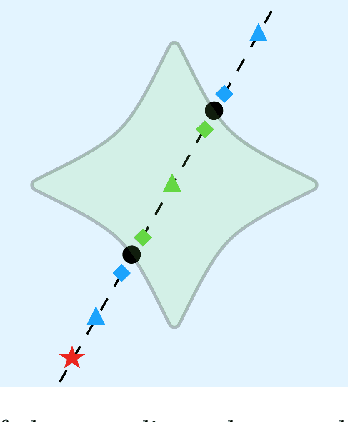
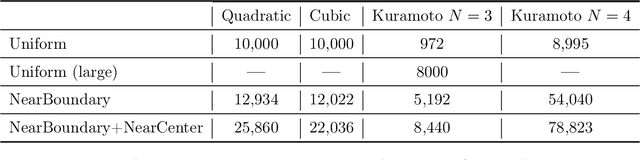
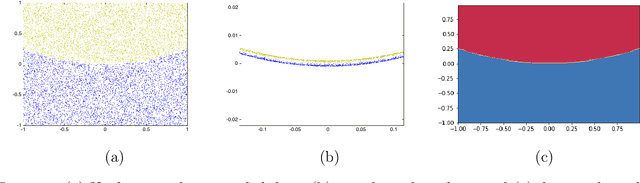
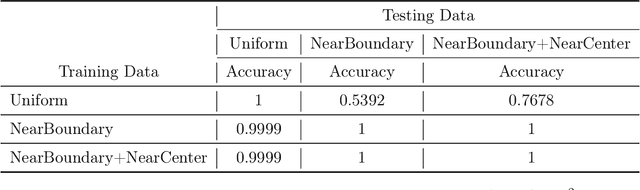
Abstract:Parameterized systems of polynomial equations arise in many applications in science and engineering with the real solutions describing, for example, equilibria of a dynamical system, linkages satisfying design constraints, and scene reconstruction in computer vision. Since different parameter values can have a different number of real solutions, the parameter space is decomposed into regions whose boundary forms the real discriminant locus. This article views locating the real discriminant locus as a supervised classification problem in machine learning where the goal is to determine classification boundaries over the parameter space, with the classes being the number of real solutions. For multidimensional parameter spaces, this article presents a novel sampling method which carefully samples the parameter space. At each sample point, homotopy continuation is used to obtain the number of real solutions to the corresponding polynomial system. Machine learning techniques including nearest neighbor and deep learning are used to efficiently approximate the real discriminant locus. One application of having learned the real discriminant locus is to develop a real homotopy method that only tracks the real solution paths unlike traditional methods which track all~complex~solution~paths. Examples show that the proposed approach can efficiently approximate complicated solution boundaries such as those arising from the equilibria of the Kuramoto model.
MCFlow: Monte Carlo Flow Models for Data Imputation
Mar 27, 2020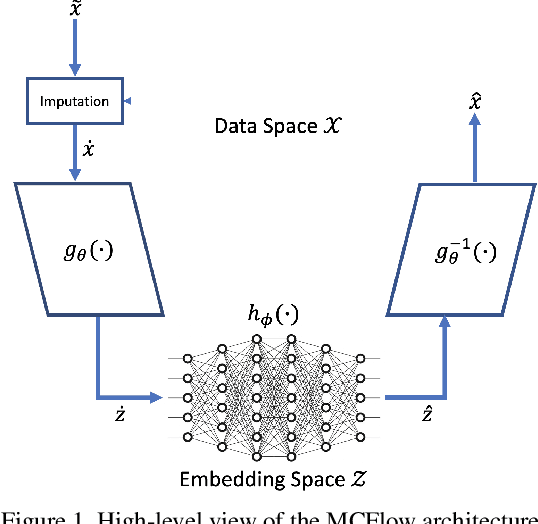
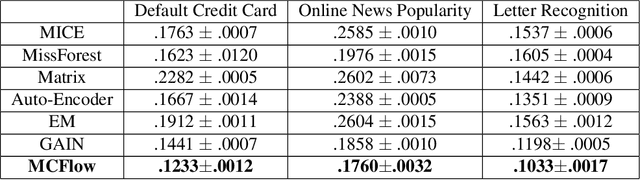
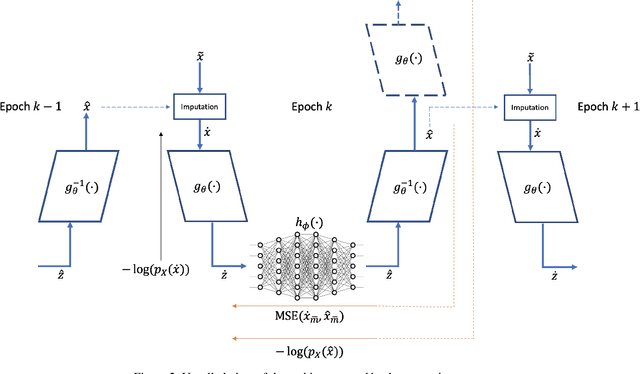
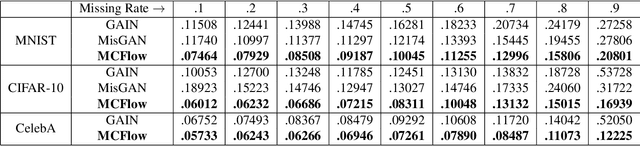
Abstract:We consider the topic of data imputation, a foundational task in machine learning that addresses issues with missing data. To that end, we propose MCFlow, a deep framework for imputation that leverages normalizing flow generative models and Monte Carlo sampling. We address the causality dilemma that arises when training models with incomplete data by introducing an iterative learning scheme which alternately updates the density estimate and the values of the missing entries in the training data. We provide extensive empirical validation of the effectiveness of the proposed method on standard multivariate and image datasets, and benchmark its performance against state-of-the-art alternatives. We demonstrate that MCFlow is superior to competing methods in terms of the quality of the imputed data, as well as with regards to its ability to preserve the semantic structure of the data.
Medical Time Series Classification with Hierarchical Attention-based Temporal Convolutional Networks: A Case Study of Myotonic Dystrophy Diagnosis
Mar 28, 2019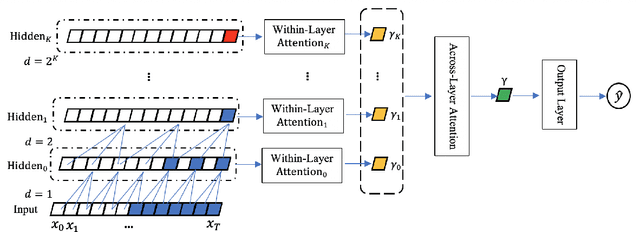
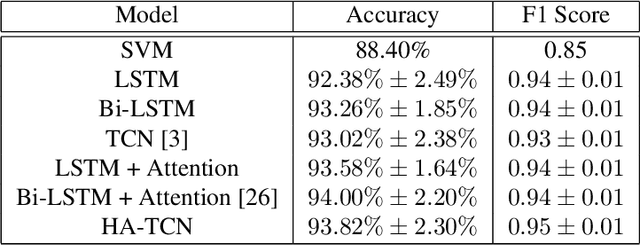
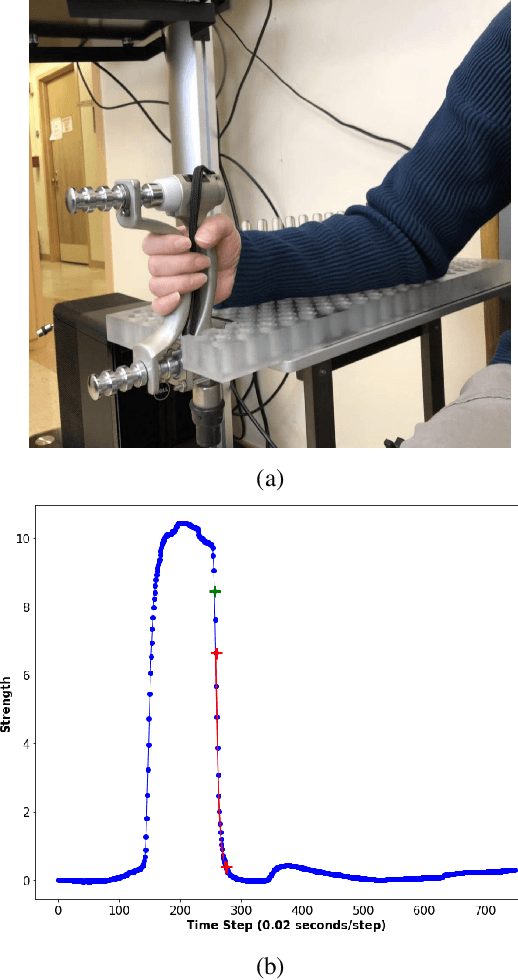
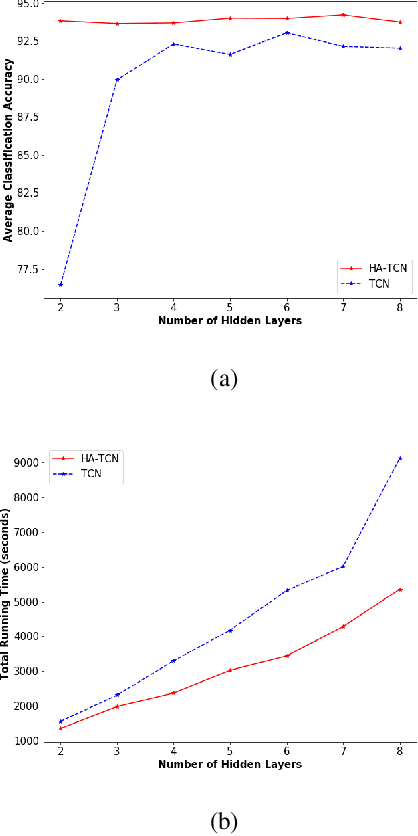
Abstract:Myotonia, which refers to delayed muscle relaxation after contraction, is the main symptom of myotonic dystrophy patients. We propose a hierarchical attention-based temporal convolutional network (HA-TCN) for myotonic dystrohpy diagnosis from handgrip time series data, and introduce mechanisms that enable model explainability. We compare the performance of the HA-TCN model against that of benchmark TCN models, LSTM models with and without attention mechanisms, and SVM approaches with handcrafted features. In terms of classification accuracy and F1 score, we found all deep learning models have similar levels of performance, and they all outperform SVM. Further, the HA-TCN model outperforms its TCN counterpart with regards to computational efficiency regardless of network depth, and in terms of performance particularly when the number of hidden layers is small. Lastly, HA-TCN models can consistently identify relevant time series segments in the relaxation phase of the handgrip time series, and exhibit increased robustness to noise when compared to attention-based LSTM models.
Towards Robust Deep Neural Networks
Oct 27, 2018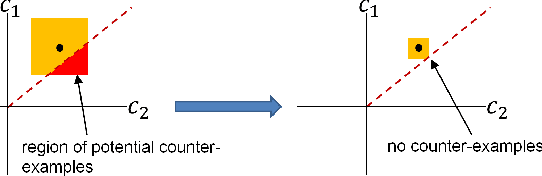
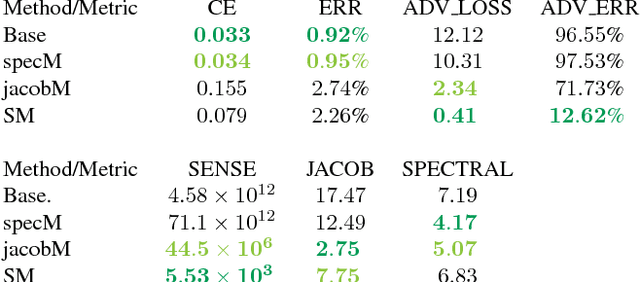
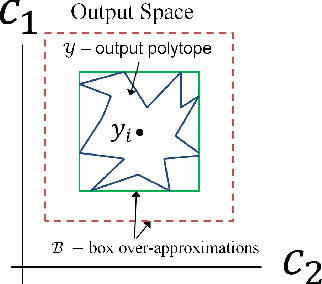

Abstract:We examine the relationship between the energy landscape of neural networks and their robustness to adversarial attacks. Combining energy landscape techniques developed in computational chemistry with tools drawn from formal methods, we produce empirical evidence that networks corresponding to lower-lying minima in the landscape tend to be more robust. The robustness measure used is the inverse of the sensitivity measure, which we define as the volume of an over-approximation of the reachable set of network outputs under all additive $l_{\infty}$ bounded perturbations on the input data. We present a novel loss function which contains a weighted sensitivity component in addition to the traditional task-oriented and regularization terms. In our experiments on standard machine learning and computer vision datasets (e.g., Iris and MNIST), we show that the proposed loss function leads to networks which reliably optimize the robustness measure as well as other related metrics of adversarial robustness without significant degradation in the classification error.
The Loss Surface of XOR Artificial Neural Networks
Apr 06, 2018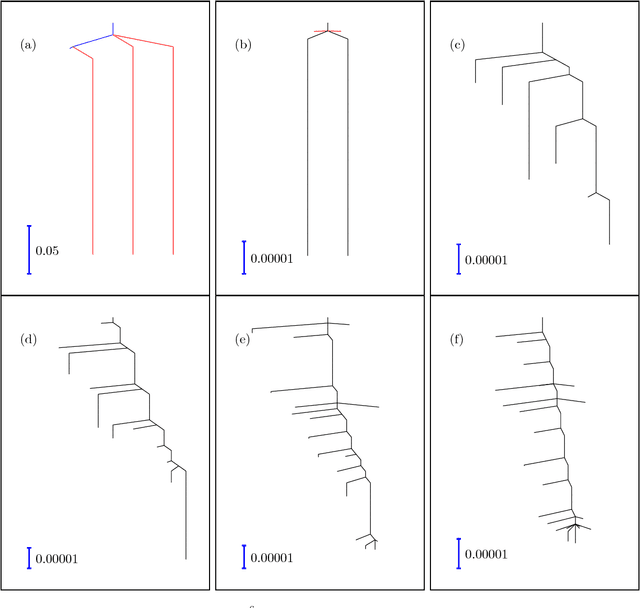
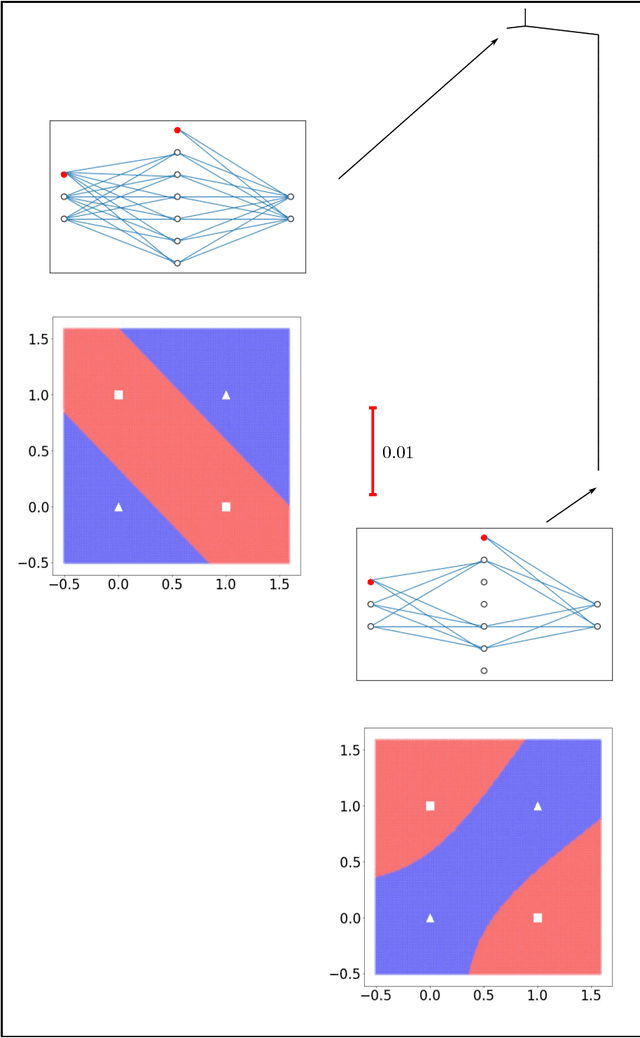
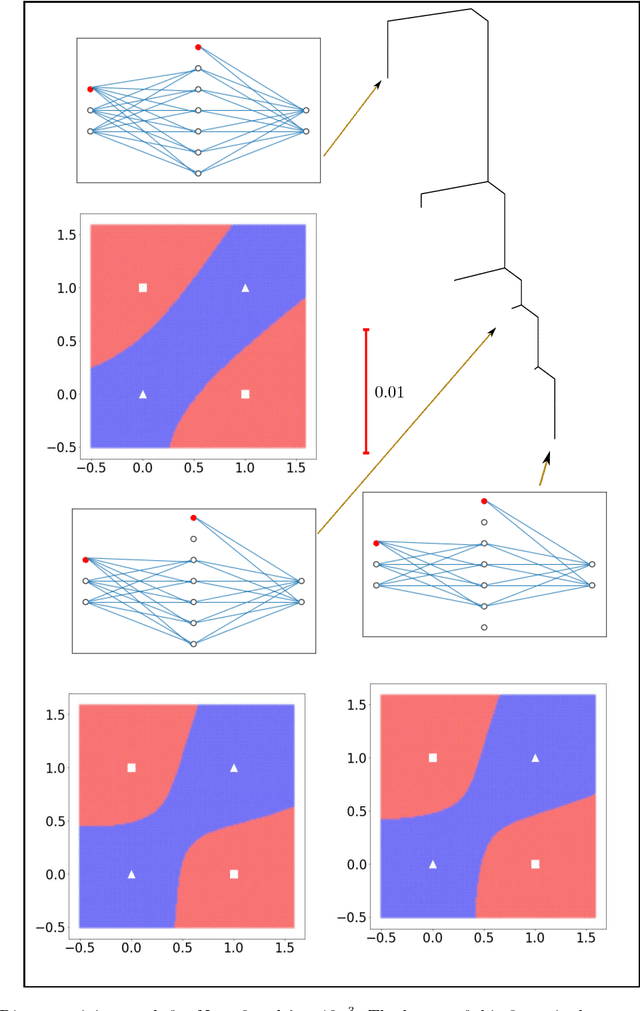
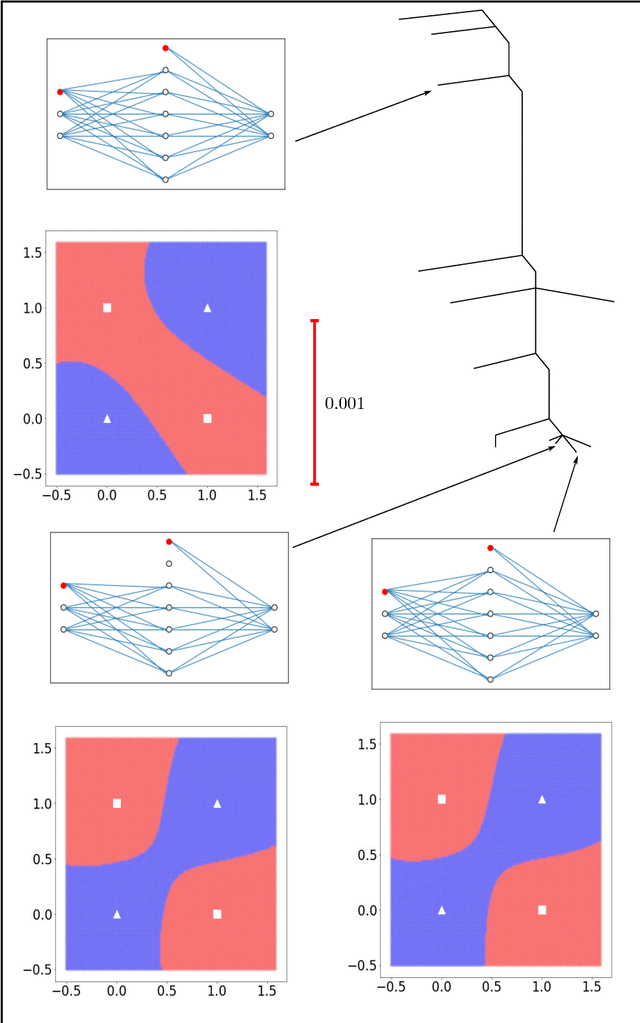
Abstract:Training an artificial neural network involves an optimization process over the landscape defined by the cost (loss) as a function of the network parameters. We explore these landscapes using optimisation tools developed for potential energy landscapes in molecular science. The number of local minima and transition states (saddle points of index one), as well as the ratio of transition states to minima, grow rapidly with the number of nodes in the network. There is also a strong dependence on the regularisation parameter, with the landscape becoming more convex (fewer minima) as the regularisation term increases. We demonstrate that in our formulation, stationary points for networks with $N_h$ hidden nodes, including the minimal network required to fit the XOR data, are also stationary points for networks with $N_{h} +1$ hidden nodes when all the weights involving the additional nodes are zero. Hence, smaller networks optimized to train the XOR data are embedded in the landscapes of larger networks. Our results clarify certain aspects of the classification and sensitivity (to perturbations in the input data) of minima and saddle points for this system, and may provide insight into dropout and network compression.
* 19 pages, 6 figures. Submitted to journal in Oct, 2017
Deep Multimodal Representation Learning from Temporal Data
Apr 11, 2017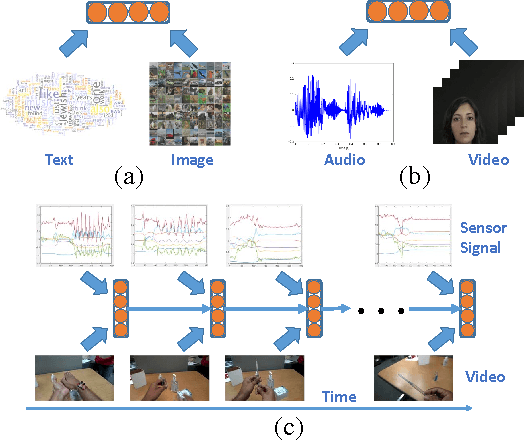
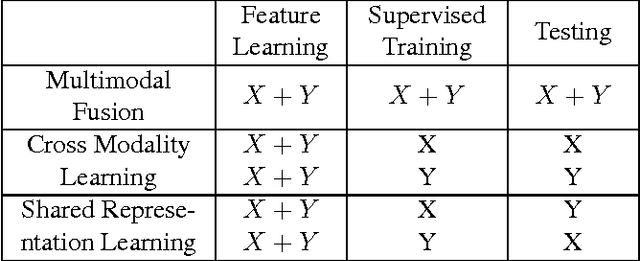
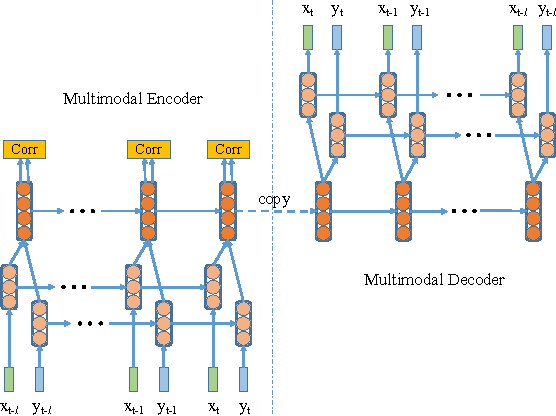

Abstract:In recent years, Deep Learning has been successfully applied to multimodal learning problems, with the aim of learning useful joint representations in data fusion applications. When the available modalities consist of time series data such as video, audio and sensor signals, it becomes imperative to consider their temporal structure during the fusion process. In this paper, we propose the Correlational Recurrent Neural Network (CorrRNN), a novel temporal fusion model for fusing multiple input modalities that are inherently temporal in nature. Key features of our proposed model include: (i) simultaneous learning of the joint representation and temporal dependencies between modalities, (ii) use of multiple loss terms in the objective function, including a maximum correlation loss term to enhance learning of cross-modal information, and (iii) the use of an attention model to dynamically adjust the contribution of different input modalities to the joint representation. We validate our model via experimentation on two different tasks: video- and sensor-based activity classification, and audio-visual speech recognition. We empirically analyze the contributions of different components of the proposed CorrRNN model, and demonstrate its robustness, effectiveness and state-of-the-art performance on multiple datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge