HomOpt: A Homotopy-Based Hyperparameter Optimization Method

Machine learning has achieved remarkable success over the past couple of decades, often attributed to a combination of algorithmic innovations and the availability of high-quality data available at scale. However, a third critical component is the fine-tuning of hyperparameters, which plays a pivotal role in achieving optimal model performance. Despite its significance, hyperparameter optimization (HPO) remains a challenging task for several reasons. Many HPO techniques rely on naive search methods or assume that the loss function is smooth and continuous, which may not always be the case. Traditional methods, like grid search and Bayesian optimization, often struggle to quickly adapt and efficiently search the loss landscape. Grid search is computationally expensive, while Bayesian optimization can be slow to prime. Since the search space for HPO is frequently high-dimensional and non-convex, it is often challenging to efficiently find a global minimum. Moreover, optimal hyperparameters can be sensitive to the specific dataset or task, further complicating the search process. To address these issues, we propose a new hyperparameter optimization method, HomOpt, using a data-driven approach based on a generalized additive model (GAM) surrogate combined with homotopy optimization. This strategy augments established optimization methodologies to boost the performance and effectiveness of any given method with faster convergence to the optimum on continuous, discrete, and categorical domain spaces. We compare the effectiveness of HomOpt applied to multiple optimization techniques (e.g., Random Search, TPE, Bayes, and SMAC) showing improved objective performance on many standardized machine learning benchmarks and challenging open-set recognition tasks.

LINFA: a Python library for variational inference with normalizing flow and annealing

Variational inference is an increasingly popular method in statistics and machine learning for approximating probability distributions. We developed LINFA (Library for Inference with Normalizing Flow and Annealing), a Python library for variational inference to accommodate computationally expensive models and difficult-to-sample distributions with dependent parameters. We discuss the theoretical background, capabilities, and performance of LINFA in various benchmarks. LINFA is publicly available on GitHub at https://github.com/desResLab/LINFA.

Output Mode Switching for Parallel Five-bar Manipulators Using a Graph-based Path Planner

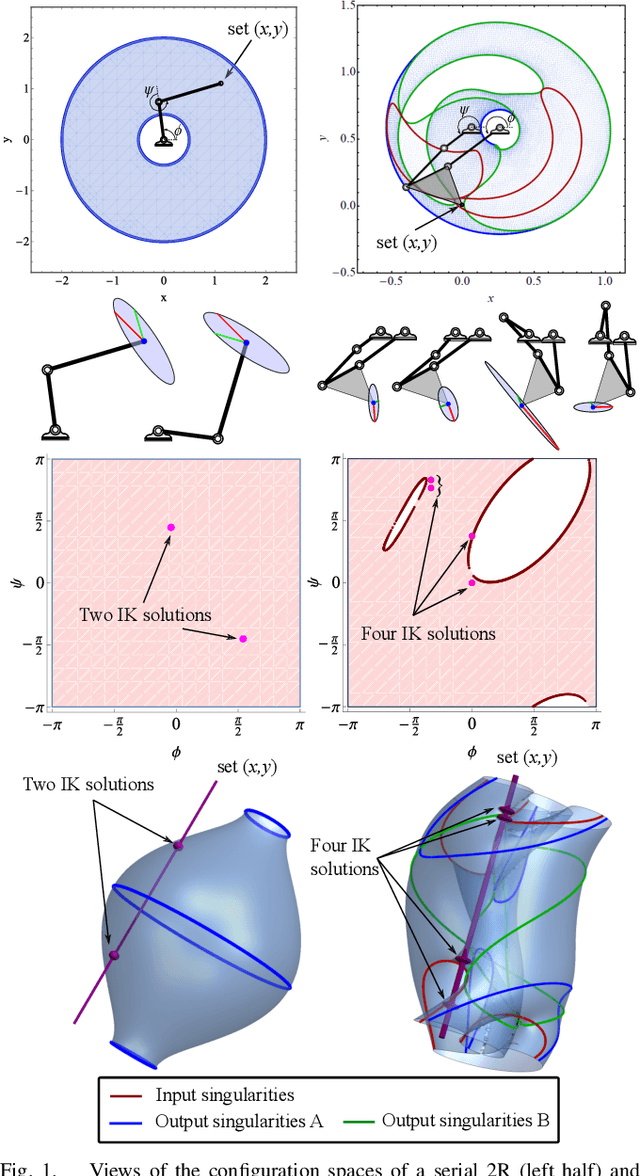
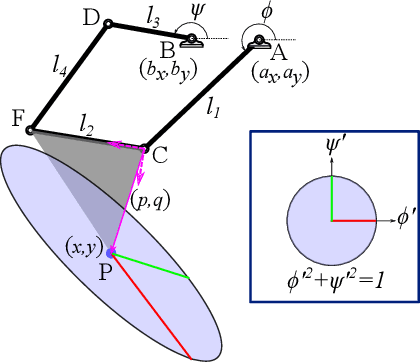
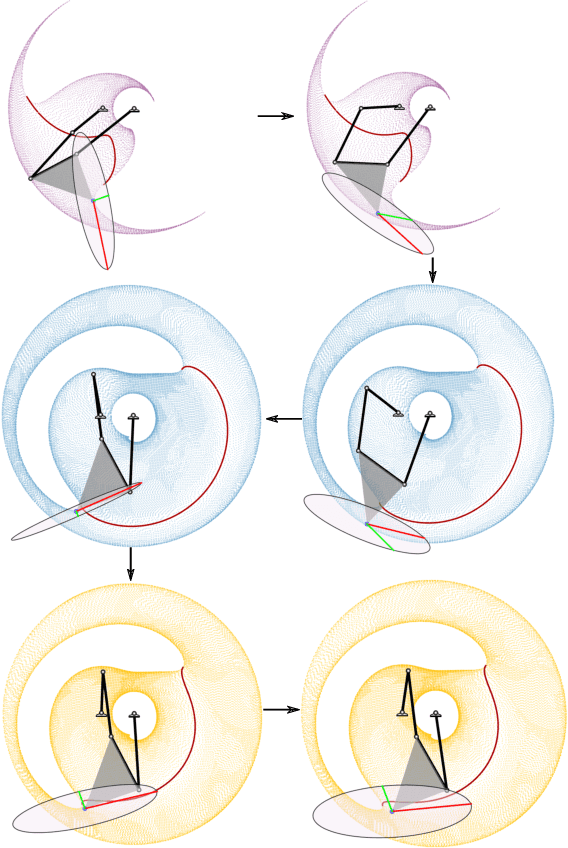
The configuration manifolds of parallel manipulators exhibit more nonlinearity than serial manipulators. Qualitatively, they can be seen to possess extra folds. By projecting such manifolds onto spaces of engineering relevance, such as an output workspace or an input actuator space, these folds cast edges that exhibit nonsmooth behavior. For example, inside the global workspace bounds of a five-bar linkage appear several local workspace bounds that only constrain certain output modes of the mechanism. The presence of such boundaries, which manifest in both input and output projections, serve as a source of confusion when these projections are studied exclusively instead of the configuration manifold itself. Particularly, the design of nonsymmetric parallel manipulators has been confounded by the presence of exotic projections in their input and output spaces. In this paper, we represent the configuration space with a radius graph, then weight each edge by solving an optimization problem using homotopy continuation to quantify transmission quality. We then employ a graph path planner to approximate geodesics between configuration points that avoid regions of low transmission quality. Our methodology automatically generates paths capable of transitioning between non-neighboring output modes, a motion which involves osculating multiple workspace boundaries (local, global, or both). We apply our technique to two nonsymmetric five-bar examples that demonstrate how transmission properties and other characteristics of the workspace can be selected by switching output modes.

AdaAnn: Adaptive Annealing Scheduler for Probability Density Approximation

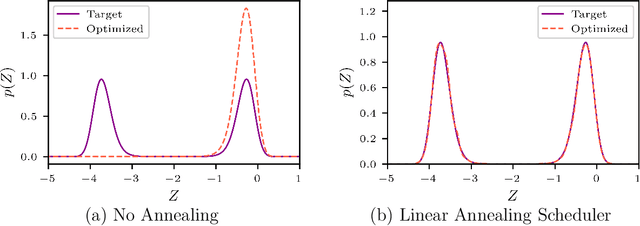
Approximating probability distributions can be a challenging task, particularly when they are supported over regions of high geometrical complexity or exhibit multiple modes. Annealing can be used to facilitate this task which is often combined with constant a priori selected increments in inverse temperature. However, using constant increments limit the computational efficiency due to the inability to adapt to situations where smooth changes in the annealed density could be handled equally well with larger increments. We introduce AdaAnn, an adaptive annealing scheduler that automatically adjusts the temperature increments based on the expected change in the Kullback-Leibler divergence between two distributions with a sufficiently close annealing temperature. AdaAnn is easy to implement and can be integrated into existing sampling approaches such as normalizing flows for variational inference and Markov chain Monte Carlo. We demonstrate the computational efficiency of the AdaAnn scheduler for variational inference with normalizing flows on a number of examples, including density approximation and parameter estimation for dynamical systems.

Machine learning the real discriminant locus

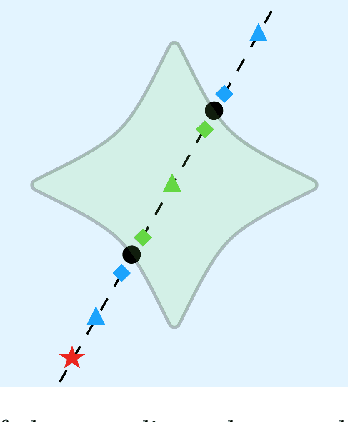
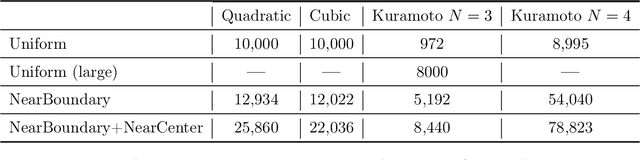
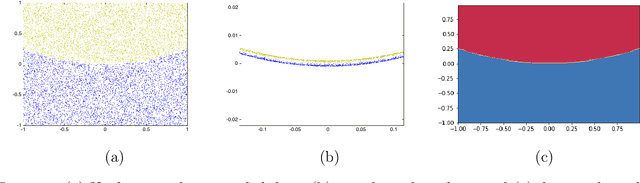
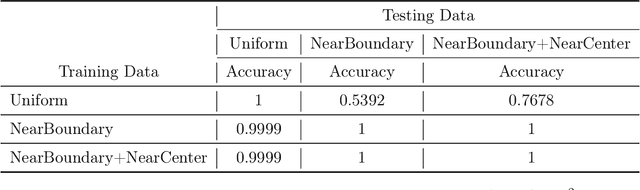
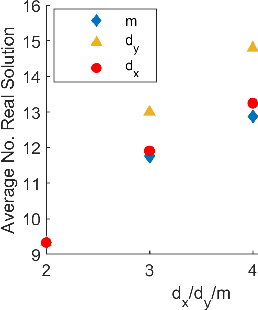
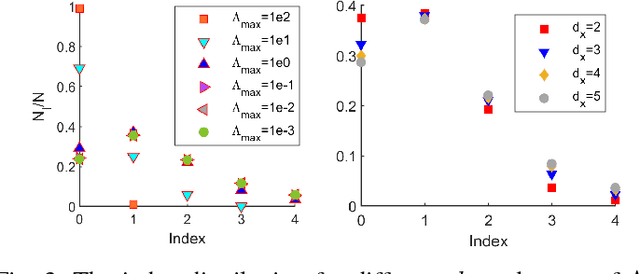
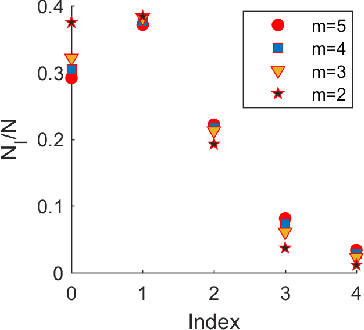
Parameterized systems of polynomial equations arise in many applications in science and engineering with the real solutions describing, for example, equilibria of a dynamical system, linkages satisfying design constraints, and scene reconstruction in computer vision. Since different parameter values can have a different number of real solutions, the parameter space is decomposed into regions whose boundary forms the real discriminant locus. This article views locating the real discriminant locus as a supervised classification problem in machine learning where the goal is to determine classification boundaries over the parameter space, with the classes being the number of real solutions. For multidimensional parameter spaces, this article presents a novel sampling method which carefully samples the parameter space. At each sample point, homotopy continuation is used to obtain the number of real solutions to the corresponding polynomial system. Machine learning techniques including nearest neighbor and deep learning are used to efficiently approximate the real discriminant locus. One application of having learned the real discriminant locus is to develop a real homotopy method that only tracks the real solution paths unlike traditional methods which track all~complex~solution~paths. Examples show that the proposed approach can efficiently approximate complicated solution boundaries such as those arising from the equilibria of the Kuramoto model.

Using monodromy to statistically estimate the number of solutions

Synthesis problems for linkages in kinematics often yield large structured parameterized polynomial systems which generically have far fewer solutions than traditional upper bounds would suggest. This paper describes statistical models for estimating the generic number of solutions of such parameterized polynomial systems. The new approach extends previous work on success ratios of parameter homotopies to using monodromy loops as well as the addition of a trace test that provides a stopping criterion for validating that all solutions have been found. Several examples are presented demonstrating the method including Watt I six-bar motion generation problems.

The loss surface of deep linear networks viewed through the algebraic geometry lens

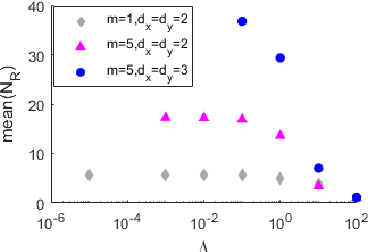
By using the viewpoint of modern computational algebraic geometry, we explore properties of the optimization landscapes of the deep linear neural network models. After clarifying on the various definitions of "flat" minima, we show that the geometrically flat minima, which are merely artifacts of residual continuous symmetries of the deep linear networks, can be straightforwardly removed by a generalized $L_2$ regularization. Then, we establish upper bounds on the number of isolated stationary points of these networks with the help of algebraic geometry. Using these upper bounds and utilizing a numerical algebraic geometry method, we find all stationary points of modest depth and matrix size. We show that in the presence of the non-zero regularization, deep linear networks indeed possess local minima which are not the global minima. Our computational results clarify certain aspects of the loss surfaces of deep linear networks and provide novel insights.