Galois/monodromy groups for decomposing minimal problems in 3D reconstruction

We consider Galois/monodromy groups arising in computer vision applications, with a view towards building more efficient polynomial solvers. The Galois/monodromy group allows us to decide when a given problem decomposes into algebraic subproblems, and whether or not it has any symmetries. Tools from numerical algebraic geometry and computational group theory allow us to apply this framework to classical and novel reconstruction problems. We consider three classical cases--3-point absolute pose, 5-point relative pose, and 4-point homography estimation for calibrated cameras--where the decomposition and symmetries may be naturally understood in terms of the Galois/monodromy group. We then show how our framework can be applied to novel problems from absolute and relative pose estimation. For instance, we discover new symmetries for absolute pose problems involving mixtures of point and line features. We also describe a problem of estimating a pair of calibrated homographies between three images. For this problem of degree 64, we can reduce the degree to 16; the latter better reflecting the intrinsic difficulty of algebraically solving the problem. As a byproduct, we obtain new constraints on compatible homographies, which may be of independent interest.

Machine learning the real discriminant locus

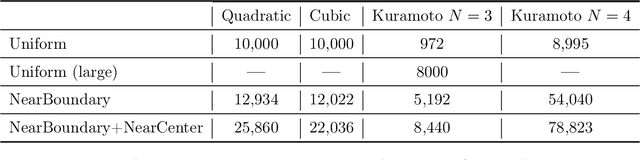
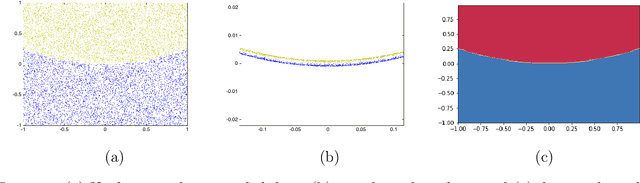
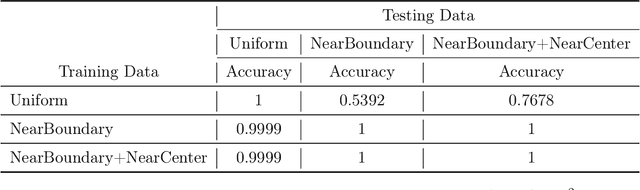
Parameterized systems of polynomial equations arise in many applications in science and engineering with the real solutions describing, for example, equilibria of a dynamical system, linkages satisfying design constraints, and scene reconstruction in computer vision. Since different parameter values can have a different number of real solutions, the parameter space is decomposed into regions whose boundary forms the real discriminant locus. This article views locating the real discriminant locus as a supervised classification problem in machine learning where the goal is to determine classification boundaries over the parameter space, with the classes being the number of real solutions. For multidimensional parameter spaces, this article presents a novel sampling method which carefully samples the parameter space. At each sample point, homotopy continuation is used to obtain the number of real solutions to the corresponding polynomial system. Machine learning techniques including nearest neighbor and deep learning are used to efficiently approximate the real discriminant locus. One application of having learned the real discriminant locus is to develop a real homotopy method that only tracks the real solution paths unlike traditional methods which track all~complex~solution~paths. Examples show that the proposed approach can efficiently approximate complicated solution boundaries such as those arising from the equilibria of the Kuramoto model.