Minimal Perspective Autocalibration

We introduce a new family of minimal problems for reconstruction from multiple views. Our primary focus is a novel approach to autocalibration, a long-standing problem in computer vision. Traditional approaches to this problem, such as those based on Kruppa's equations or the modulus constraint, rely explicitly on the knowledge of multiple fundamental matrices or a projective reconstruction. In contrast, we consider a novel formulation involving constraints on image points, the unknown depths of 3D points, and a partially specified calibration matrix $K$. For $2$ and $3$ views, we present a comprehensive taxonomy of minimal autocalibration problems obtained by relaxing some of these constraints. These problems are organized into classes according to the number of views and any assumed prior knowledge of $K$. Within each class, we determine problems with the fewest -- or a relatively small number of -- solutions. From this zoo of problems, we devise three practical solvers. Experiments with synthetic and real data and interfacing our solvers with COLMAP demonstrate that we achieve superior accuracy compared to state-of-the-art calibration methods. The code is available at https://github.com/andreadalcin/MinimalPerspectiveAutocalibration

Efficient Solution of Point-Line Absolute Pose

We revisit certain problems of pose estimation based on 3D--2D correspondences between features which may be points or lines. Specifically, we address the two previously-studied minimal problems of estimating camera extrinsics from $p \in \{ 1, 2 \}$ point--point correspondences and $l=3-p$ line--line correspondences. To the best of our knowledge, all of the previously-known practical solutions to these problems required computing the roots of degree $\ge 4$ (univariate) polynomials when $p=2$, or degree $\ge 8$ polynomials when $p=1.$ We describe and implement two elementary solutions which reduce the degrees of the needed polynomials from $4$ to $2$ and from $8$ to $4$, respectively. We show experimentally that the resulting solvers are numerically stable and fast: when compared to the previous state-of-the art, we may obtain nearly an order of magnitude speedup. The code is available at \url{https://github.com/petrhruby97/efficient\_absolute}

Algebra and Geometry of Camera Resectioning

We study algebraic varieties associated with the camera resectioning problem. We characterize these resectioning varieties' multigraded vanishing ideals using Gr\"obner basis techniques. As an application, we derive and re-interpret celebrated results in geometric computer vision related to camera-point duality. We also clarify some relationships between the classical problems of optimal resectioning and triangulation, state a conjectural formula for the Euclidean distance degree of the resectioning variety, and discuss how this conjecture relates to the recently-resolved multiview conjecture.

An Atlas for the Pinhole Camera

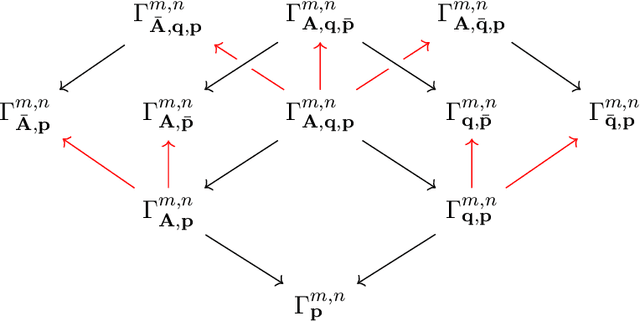
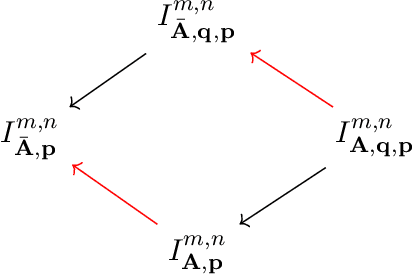
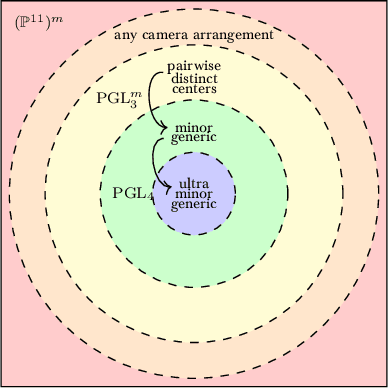
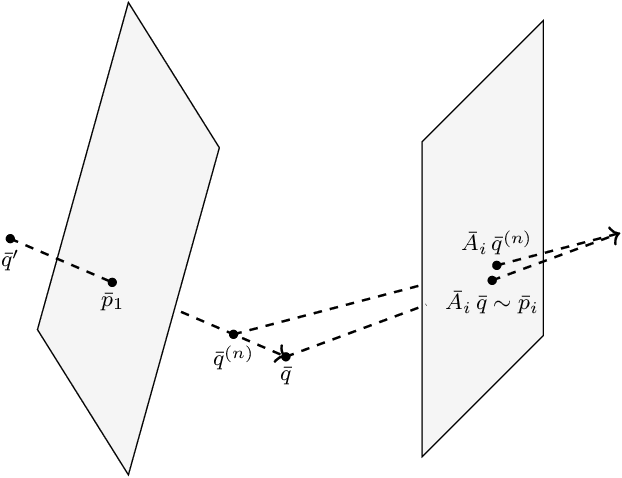
We introduce an atlas of algebro-geometric objects associated with image formation in pinhole cameras. The nodes of the atlas are algebraic varieties or their vanishing ideals related to each other by projection or elimination and restriction or specialization respectively. This atlas offers a unifying framework for the study of problems in 3D computer vision. We initiate the study of the atlas by completely characterizing a part of the atlas stemming from the triangulation problem. We conclude with several open problems and generalizations of the atlas.

Learning to Solve Hard Minimal Problems

We present an approach to solving hard geometric optimization problems in the RANSAC framework. The hard minimal problems arise from relaxing the original geometric optimization problem into a minimal problem with many spurious solutions. Our approach avoids computing large numbers of spurious solutions. We design a learning strategy for selecting a starting problem-solution pair that can be numerically continued to the problem and the solution of interest. We demonstrate our approach by developing a RANSAC solver for the problem of computing the relative pose of three calibrated cameras, via a minimal relaxation using four points in each view. On average, we can solve a single problem in under 70 $\mu s.$ We also benchmark and study our engineering choices on the very familiar problem of computing the relative pose of two calibrated cameras, via the minimal case of five points in two views.

Galois/monodromy groups for decomposing minimal problems in 3D reconstruction

We consider Galois/monodromy groups arising in computer vision applications, with a view towards building more efficient polynomial solvers. The Galois/monodromy group allows us to decide when a given problem decomposes into algebraic subproblems, and whether or not it has any symmetries. Tools from numerical algebraic geometry and computational group theory allow us to apply this framework to classical and novel reconstruction problems. We consider three classical cases--3-point absolute pose, 5-point relative pose, and 4-point homography estimation for calibrated cameras--where the decomposition and symmetries may be naturally understood in terms of the Galois/monodromy group. We then show how our framework can be applied to novel problems from absolute and relative pose estimation. For instance, we discover new symmetries for absolute pose problems involving mixtures of point and line features. We also describe a problem of estimating a pair of calibrated homographies between three images. For this problem of degree 64, we can reduce the degree to 16; the latter better reflecting the intrinsic difficulty of algebraically solving the problem. As a byproduct, we obtain new constraints on compatible homographies, which may be of independent interest.

PL${}_{1}$P -- Point-line Minimal Problems under Partial Visibility in Three Views

We present a complete classification of minimal problems for generic arrangements of points and lines in space observed partially by three calibrated perspective cameras when each line is incident to at most one point. This is a large class of interesting minimal problems that allows missing observations in images due to occlusions and missed detections. There is an infinite number of such minimal problems; however, we show that they can be reduced to 140616 equivalence classes by removing superfluous features and relabeling the cameras. We also introduce camera-minimal problems, which are practical for designing minimal solvers, and show how to pick a simplest camera-minimal problem for each minimal problem. This simplification results in 74575 equivalence classes. Only 76 of these were known; the rest are new. In order to identify problems that have potential for practical solving of image matching and 3D reconstruction, we present several smaller natural subfamilies of camera-minimal problems as well as compute solution counts for all camera-minimal problems which have less than 300 solutions for generic data.

Trifocal Relative Pose from Lines at Points and its Efficient Solution

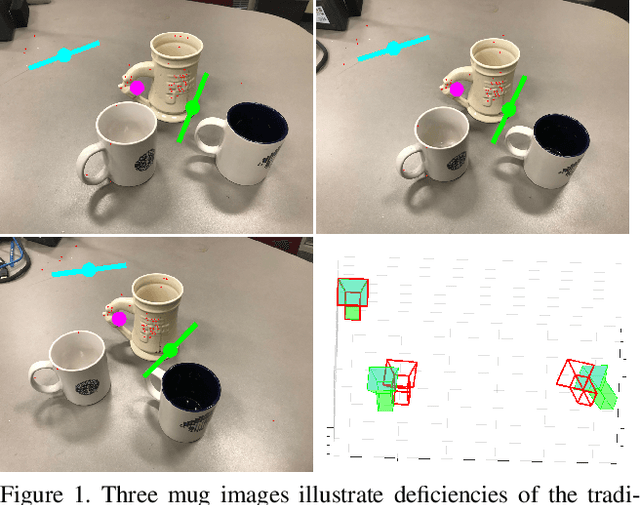
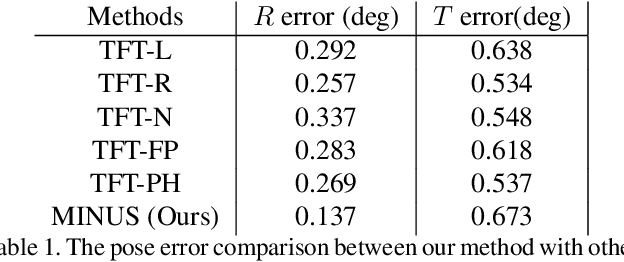
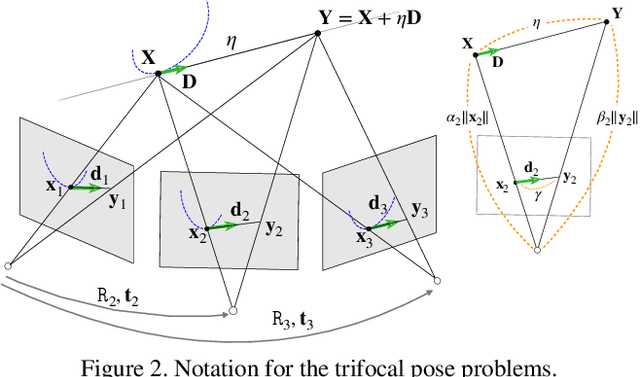
We present a new minimal problem for relative pose estimation mixing point features with lines incident at points observed in three views and its efficient homotopy continuation solver. We demonstrate the generality of the approach by analyzing and solving an additional problem with mixed point and line correspondences in three views. The minimal problems include correspondences of (i) three points and one line and (ii) three points and two lines through two of the points which is reported and analyzed here for the first time. These are difficult to solve, as they have 216 and - as shown here - 312 solutions, but cover important practical situations when line and point features appear together, e.g., in urban scenes or when observing curves. We demonstrate that even such difficult problems can be solved robustly using a suitable homotopy continuation technique and we provide an implementation optimized for minimal problems that can be integrated into engineering applications. Our simulated and real experiments demonstrate our solvers in the camera geometry computation task in structure from motion. We show that new solvers allow for reconstructing challenging scenes where the standard two-view initialization of structure from motion fails.

PLMP - Point-Line Minimal Problems in Complete Multi-View Visibility

We present a complete classification of all minimal problems for generic arrangements of points and lines completely observed by calibrated perspective cameras. We show that there are only 30 minimal problems in total, no problems exist for more than 6 cameras, for more than 5 points, and for more than 6 lines. We present a sequence of tests for detecting minimality starting with counting degrees of freedom and ending with full symbolic and numeric verification of representative examples. For all minimal problems discovered, we present their algebraic degrees, i.e. the number of solutions, which measure their intrinsic difficulty. Our classification shows that there are many interesting new minimal problems. Our results also show how exactly the difficulty of problems grows with the number of views. Importantly, we discovered several new minimal problems with small degrees that might be practical in image matching and 3D reconstruction.