State estimation of a moving frequency source from observations at multiple receivers

The task of position and velocity estimation of a moving transmitter (with either a known or unknown frequency) is a common problem arising in many different application domains. Based on the Doppler effect, this work presents a direct solution using only the frequency measured by a multitude of receivers with a known state. A natural rewriting of the problem as a system of polynomial equations allows for the use of homotopy continuation to find the global solution without any a priori information about the frequency source. We show that the data from six or seven receivers is sufficient in case of known or unknown frequency, respectively. After a brief development of the mathematics, two simple examples are provided: (1) position and velocity estimation of a vocalizing dolphin emitting an acoustic signal and (2) initial orbit determination of a satellite emitting an electromagnetic signal.

Learning to Solve Hard Minimal Problems

We present an approach to solving hard geometric optimization problems in the RANSAC framework. The hard minimal problems arise from relaxing the original geometric optimization problem into a minimal problem with many spurious solutions. Our approach avoids computing large numbers of spurious solutions. We design a learning strategy for selecting a starting problem-solution pair that can be numerically continued to the problem and the solution of interest. We demonstrate our approach by developing a RANSAC solver for the problem of computing the relative pose of three calibrated cameras, via a minimal relaxation using four points in each view. On average, we can solve a single problem in under 70 $\mu s.$ We also benchmark and study our engineering choices on the very familiar problem of computing the relative pose of two calibrated cameras, via the minimal case of five points in two views.

PL${}_{1}$P -- Point-line Minimal Problems under Partial Visibility in Three Views

We present a complete classification of minimal problems for generic arrangements of points and lines in space observed partially by three calibrated perspective cameras when each line is incident to at most one point. This is a large class of interesting minimal problems that allows missing observations in images due to occlusions and missed detections. There is an infinite number of such minimal problems; however, we show that they can be reduced to 140616 equivalence classes by removing superfluous features and relabeling the cameras. We also introduce camera-minimal problems, which are practical for designing minimal solvers, and show how to pick a simplest camera-minimal problem for each minimal problem. This simplification results in 74575 equivalence classes. Only 76 of these were known; the rest are new. In order to identify problems that have potential for practical solving of image matching and 3D reconstruction, we present several smaller natural subfamilies of camera-minimal problems as well as compute solution counts for all camera-minimal problems which have less than 300 solutions for generic data.

Trifocal Relative Pose from Lines at Points and its Efficient Solution

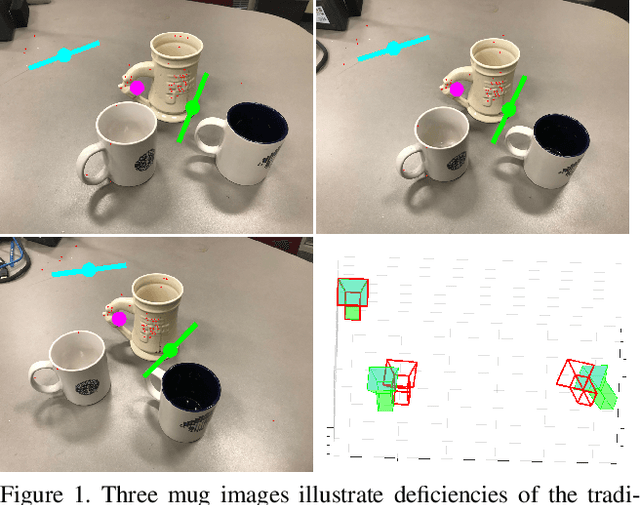
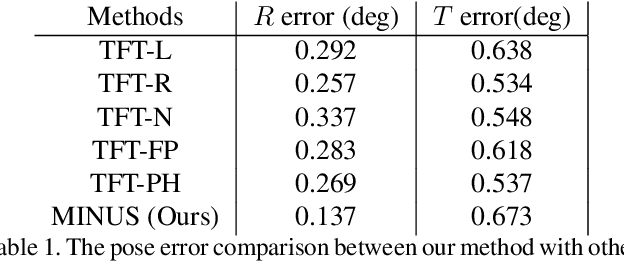
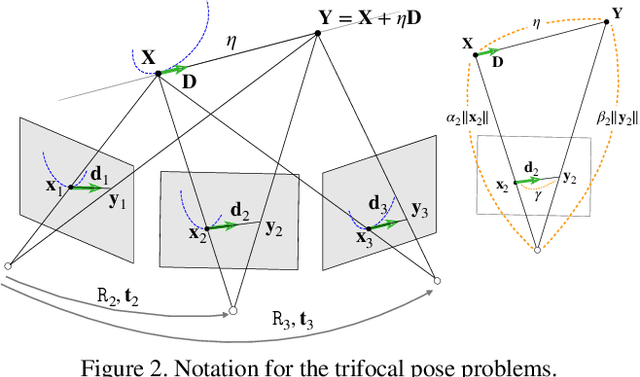
We present a new minimal problem for relative pose estimation mixing point features with lines incident at points observed in three views and its efficient homotopy continuation solver. We demonstrate the generality of the approach by analyzing and solving an additional problem with mixed point and line correspondences in three views. The minimal problems include correspondences of (i) three points and one line and (ii) three points and two lines through two of the points which is reported and analyzed here for the first time. These are difficult to solve, as they have 216 and - as shown here - 312 solutions, but cover important practical situations when line and point features appear together, e.g., in urban scenes or when observing curves. We demonstrate that even such difficult problems can be solved robustly using a suitable homotopy continuation technique and we provide an implementation optimized for minimal problems that can be integrated into engineering applications. Our simulated and real experiments demonstrate our solvers in the camera geometry computation task in structure from motion. We show that new solvers allow for reconstructing challenging scenes where the standard two-view initialization of structure from motion fails.

PLMP - Point-Line Minimal Problems in Complete Multi-View Visibility

We present a complete classification of all minimal problems for generic arrangements of points and lines completely observed by calibrated perspective cameras. We show that there are only 30 minimal problems in total, no problems exist for more than 6 cameras, for more than 5 points, and for more than 6 lines. We present a sequence of tests for detecting minimality starting with counting degrees of freedom and ending with full symbolic and numeric verification of representative examples. For all minimal problems discovered, we present their algebraic degrees, i.e. the number of solutions, which measure their intrinsic difficulty. Our classification shows that there are many interesting new minimal problems. Our results also show how exactly the difficulty of problems grows with the number of views. Importantly, we discovered several new minimal problems with small degrees that might be practical in image matching and 3D reconstruction.