Crater Projection in Linear Pushbroom Camera Images

Scientific imaging of the Moon, Mars, and other celestial bodies is often accomplished with pushbroom cameras. Craters with elliptical rims are common objects of interest within the images produced by such sensors. This work provides a framework to analyze the appearance of crater rims in pushbroom images. With knowledge of only common ellipse parameters describing the crater rim, explicit formulations are developed and shown to be convenient for drawing the apparent crater in pushbroom images. Implicit forms are also developed and indicate the orbital conditions under which craters form conics in images. Several numerical examples are provided which demonstrate how different forms of crater rim projections can be interpreted and used in practice.

State estimation of a moving frequency source from observations at multiple receivers

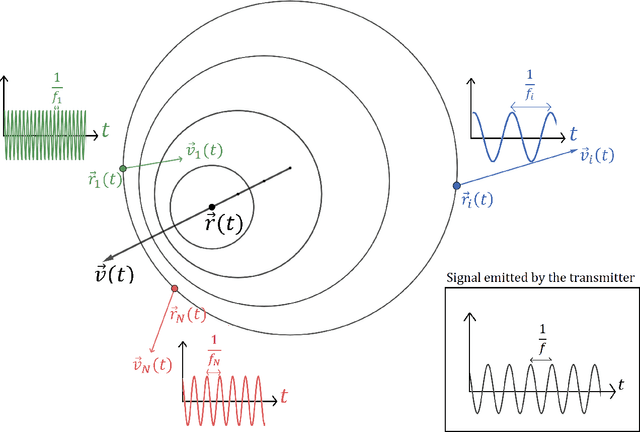
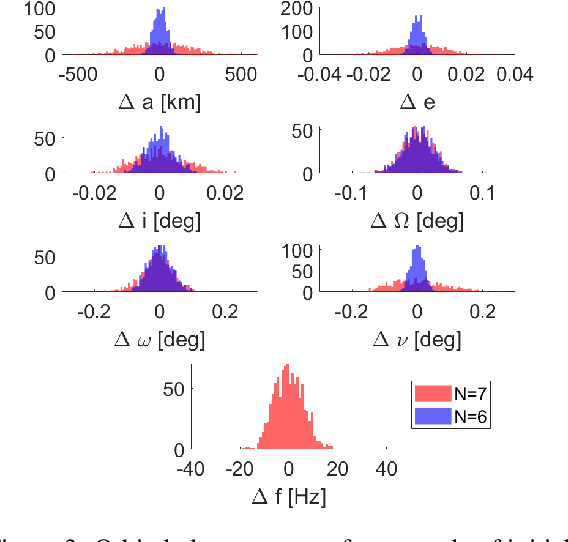
The task of position and velocity estimation of a moving transmitter (with either a known or unknown frequency) is a common problem arising in many different application domains. Based on the Doppler effect, this work presents a direct solution using only the frequency measured by a multitude of receivers with a known state. A natural rewriting of the problem as a system of polynomial equations allows for the use of homotopy continuation to find the global solution without any a priori information about the frequency source. We show that the data from six or seven receivers is sufficient in case of known or unknown frequency, respectively. After a brief development of the mathematics, two simple examples are provided: (1) position and velocity estimation of a vocalizing dolphin emitting an acoustic signal and (2) initial orbit determination of a satellite emitting an electromagnetic signal.