Optimal DLT-based Solutions for the Perspective-n-Point

We propose a modified normalized direct linear transform (DLT) algorithm for solving the perspective-n-point (PnP) problem with much better behavior than the conventional DLT. The modification consists of analytically weighting the different measurements in the linear system with a negligible increase in computational load. Our approach exhibits clear improvements -- in both performance and runtime -- when compared to popular methods such as EPnP, CPnP, RPnP, and OPnP. Our new non-iterative solution approaches that of the true optimal found via Gauss-Newton optimization, but at a fraction of the computational cost. Our optimal DLT (oDLT) implementation, as well as the experiments, are released in open source.

LOSTU: Fast, Scalable, and Uncertainty-Aware Triangulation

Triangulation algorithms often aim to minimize the reprojection ($L_2$) error, but this only provides the maximum likelihood estimate when there are no errors in the camera parameters or camera poses. Although recent advancements have yielded techniques to estimate camera parameters accounting for 3D point uncertainties, most structure from motion (SfM) pipelines still use older triangulation algorithms. This work leverages recent discoveries to provide a fast, scalable, and statistically optimal way to triangulate called LOSTU. Results show that LOSTU consistently produces lower 3D reconstruction errors than conventional $L_2$ triangulation methods -- often allowing LOSTU to successfully triangulate more points. Moreover, in addition to providing a better 3D reconstruction, LOSTU can be substantially faster than Levenberg-Marquardt (or similar) optimization schemes.

State estimation of a moving frequency source from observations at multiple receivers

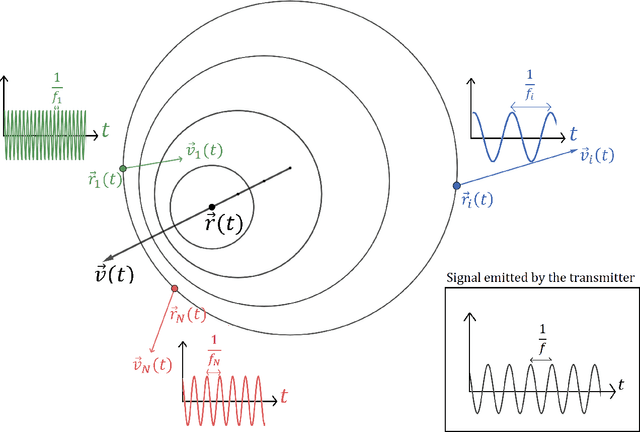
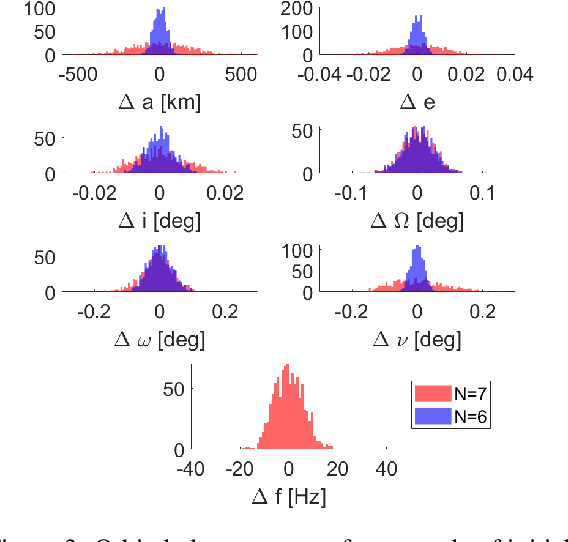
The task of position and velocity estimation of a moving transmitter (with either a known or unknown frequency) is a common problem arising in many different application domains. Based on the Doppler effect, this work presents a direct solution using only the frequency measured by a multitude of receivers with a known state. A natural rewriting of the problem as a system of polynomial equations allows for the use of homotopy continuation to find the global solution without any a priori information about the frequency source. We show that the data from six or seven receivers is sufficient in case of known or unknown frequency, respectively. After a brief development of the mathematics, two simple examples are provided: (1) position and velocity estimation of a vocalizing dolphin emitting an acoustic signal and (2) initial orbit determination of a satellite emitting an electromagnetic signal.

Pole Estimation and Optical Navigation using Circle of Latitude Projections

Images of both rotating celestial bodies (e.g., asteroids) and spheroidal planets with banded atmospheres (e.g., Jupiter) can contain features that are well-modeled as a circle of latitude (CoL). The projections of these CoLs appear as ellipses in images collected by cameras or telescopes onboard exploration spacecraft. This work shows how CoL projections may be used to determine the pole orientation and covariance for a spinning asteroid. In the case of a known planet modeled as an oblate spheroid, it is shown how similar CoL projections may be used for spacecraft localization. These methods are developed using the principles of projective geometry. Numerical results are provided for simulated images of asteroid Bennu (for pole orientation) and of Jupiter (for spacecraft localization).

Initial Orbit Determination from Only Heading Measurements

This work introduces the problem of initial orbit determination (IOD) from only heading measurements. Such a problem occurs in practice when estimating the orbit of a spacecraft using visual odometry measurements from an optical camera. After reviewing the problem geometry, a simple solution is developed in the form of an iterative scheme on the parameters describing the orbital hodograph. Numerical results are presented for an example spacecraft in low lunar orbit. The principal intent of this brief study is to communicate the existence of a new class of IOD problem to the community and to encourage the broader study of hodographs and heading-only IOD.

Absolute Triangulation Algorithms for Space Exploration

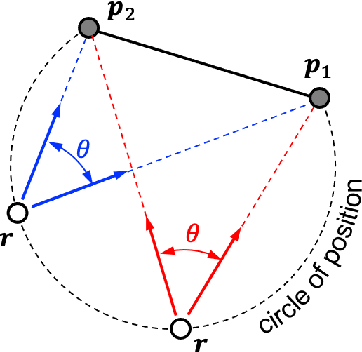
Images are an important source of information for spacecraft navigation and for three-dimensional reconstruction of observed space objects. Both of these applications take the form of a triangulation problem when the camera has a known attitude and the measurements extracted from the image are line of sight (LOS) directions. This work provides a comprehensive review of the history and theoretical foundations of triangulation. A variety of classical triangulation algorithms are reviewed, including a number of suboptimal linear methods (many LOS measurements) and the optimal method of Hartley and Sturm (only two LOS measurements). Two new optimal non-iterative triangulation algorithms are introduced that provide the same solution as Hartley and Sturm. The optimal two-measurement case can be solved as a quadratic equation in many common situations. The optimal many-measurement case may be solved without iteration as a linear system using the new Linear Optimal Sine Triangulation (LOST) method. The various triangulation algorithms are assessed with a few numerical examples, including planetary terrain relative navigation, angles-only optical navigation at Uranus, 3-D reconstruction of Notre-Dame de Paris, and angles-only relative navigation.

Lunar Crater Identification in Digital Images

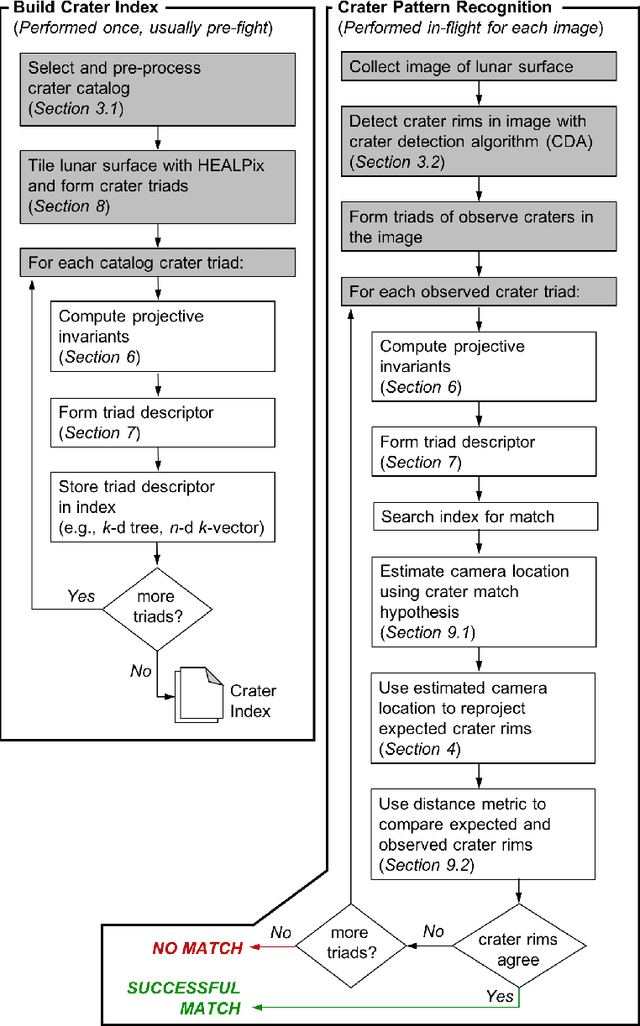
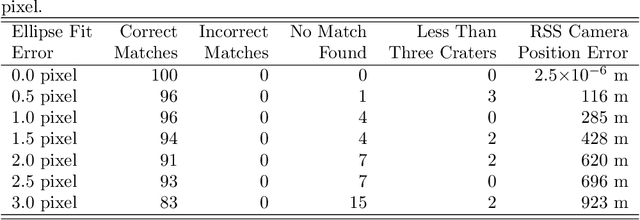
It is often necessary to identify a pattern of observed craters in a single image of the lunar surface and without any prior knowledge of the camera's location. This so-called "lost-in-space" crater identification problem is common in both crater-based terrain relative navigation (TRN) and in automatic registration of scientific imagery. Past work on crater identification has largely been based on heuristic schemes, with poor performance outside of a narrowly defined operating regime (e.g., nadir pointing images, small search areas). This work provides the first mathematically rigorous treatment of the general crater identification problem. It is shown when it is (and when it is not) possible to recognize a pattern of elliptical crater rims in an image formed by perspective projection. For the cases when it is possible to recognize a pattern, descriptors are developed using invariant theory that provably capture all of the viewpoint invariant information. These descriptors may be pre-computed for known crater patterns and placed in a searchable index for fast recognition. New techniques are also developed for computing pose from crater rim observations and for evaluating crater rim correspondences. These techniques are demonstrated on both synthetic and real images.