Tensor Denoising via Amplification and Stable Rank Methods

Tensors in the form of multilinear arrays are ubiquitous in data science applications. Captured real-world data, including video, hyperspectral images, and discretized physical systems, naturally occur as tensors and often come with attendant noise. Under the additive noise model and with the assumption that the underlying clean tensor has low rank, many denoising methods have been created that utilize tensor decomposition to effect denoising through low rank tensor approximation. However, all such decomposition methods require estimating the tensor rank, or related measures such as the tensor spectral and nuclear norms, all of which are NP-hard problems. In this work we adapt the previously developed framework of tensor amplification, which provides good approximations of the spectral and nuclear tensor norms, to denoising synthetic tensors of various sizes, ranks, and noise levels, along with real-world tensors derived from physiological signals. We also introduce denoising methods based on two variations of rank estimates called stable $X$-rank and stable slice rank. The experimental results show that in the low rank context, tensor-based amplification provides comparable denoising performance in high signal-to-noise ratio (SNR) settings and superior performance in noisy (i.e., low SNR) settings, while the stable $X$-rank method achieves superior denoising performance on the physiological signal data.

A Novel Tropical Geometry-based Interpretable Machine Learning Method: Application in Prognosis of Advanced Heart Failure

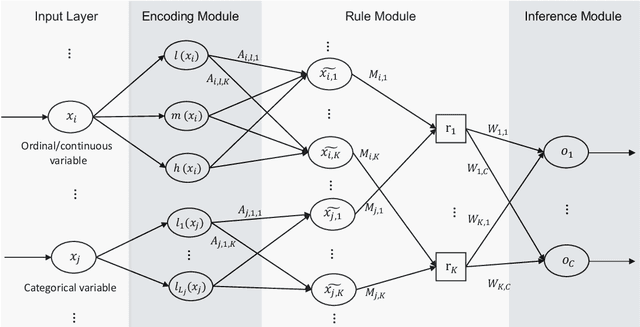
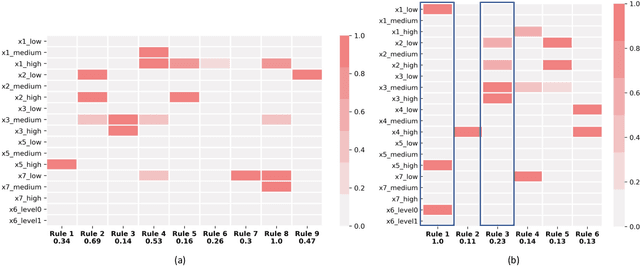
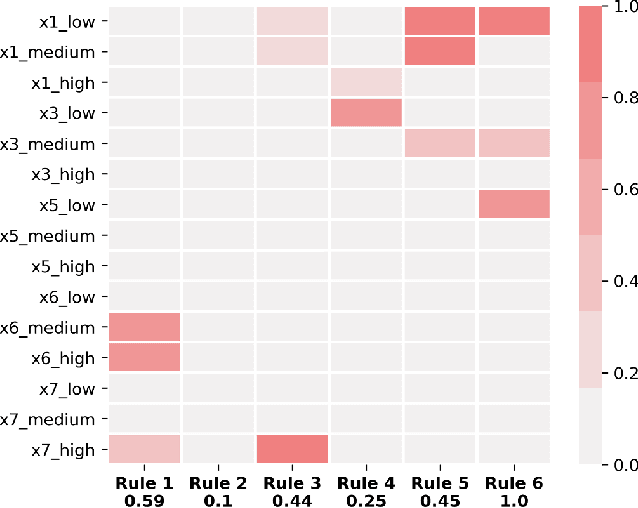
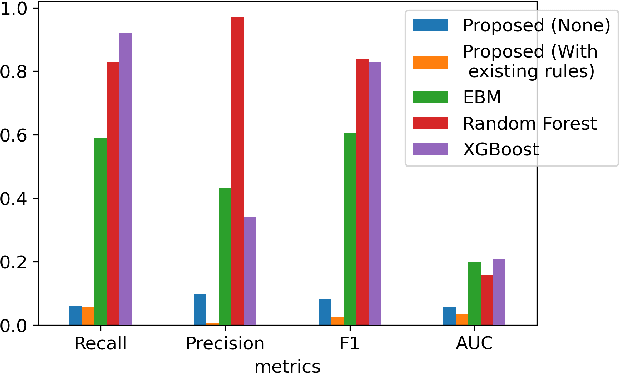
A model's interpretability is essential to many practical applications such as clinical decision support systems. In this paper, a novel interpretable machine learning method is presented, which can model the relationship between input variables and responses in humanly understandable rules. The method is built by applying tropical geometry to fuzzy inference systems, wherein variable encoding functions and salient rules can be discovered by supervised learning. Experiments using synthetic datasets were conducted to investigate the performance and capacity of the proposed algorithm in classification and rule discovery. Furthermore, the proposed method was applied to a clinical application that identified heart failure patients that would benefit from advanced therapies such as heart transplant or durable mechanical circulatory support. Experimental results show that the proposed network achieved great performance on the classification tasks. In addition to learning humanly understandable rules from the dataset, existing fuzzy domain knowledge can be easily transferred into the network and used to facilitate model training. From our results, the proposed model and the ability of learning existing domain knowledge can significantly improve the model generalizability. The characteristics of the proposed network make it promising in applications requiring model reliability and justification.

Lunar Crater Identification in Digital Images

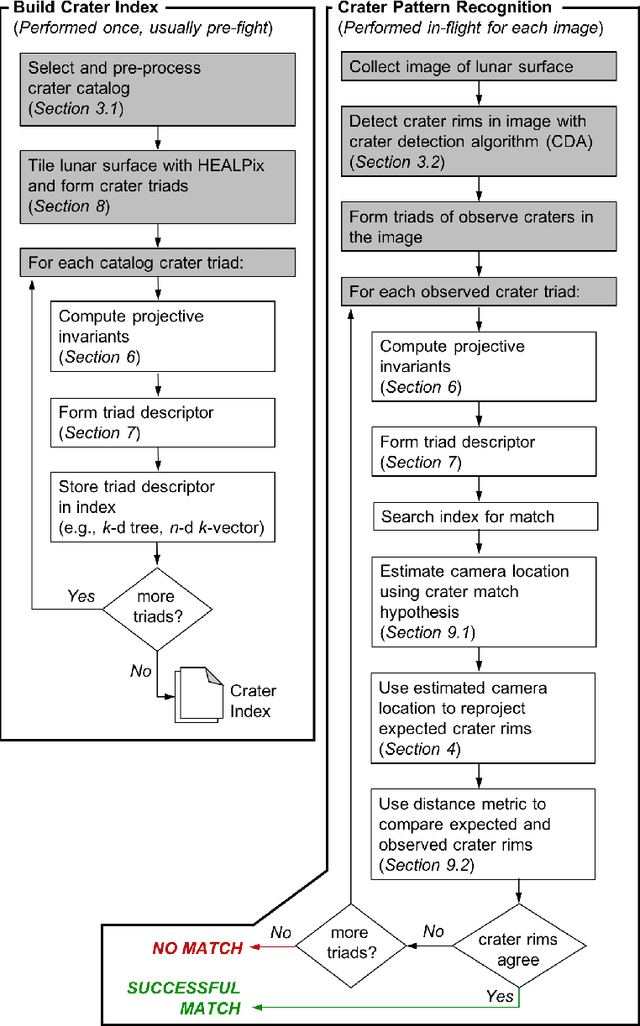
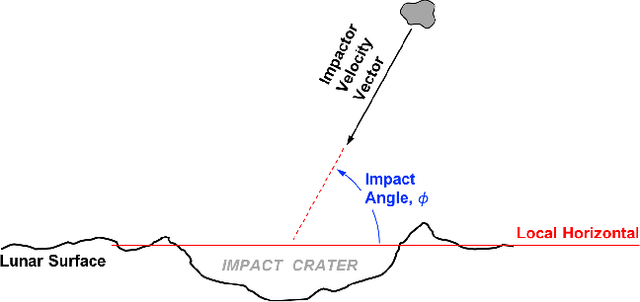
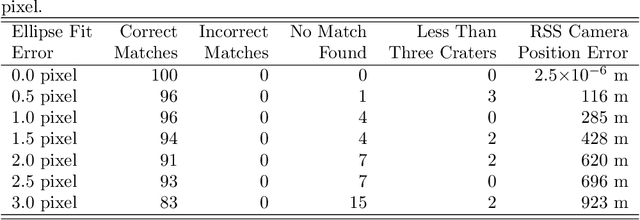
It is often necessary to identify a pattern of observed craters in a single image of the lunar surface and without any prior knowledge of the camera's location. This so-called "lost-in-space" crater identification problem is common in both crater-based terrain relative navigation (TRN) and in automatic registration of scientific imagery. Past work on crater identification has largely been based on heuristic schemes, with poor performance outside of a narrowly defined operating regime (e.g., nadir pointing images, small search areas). This work provides the first mathematically rigorous treatment of the general crater identification problem. It is shown when it is (and when it is not) possible to recognize a pattern of elliptical crater rims in an image formed by perspective projection. For the cases when it is possible to recognize a pattern, descriptors are developed using invariant theory that provably capture all of the viewpoint invariant information. These descriptors may be pre-computed for known crater patterns and placed in a searchable index for fast recognition. New techniques are also developed for computing pose from crater rim observations and for evaluating crater rim correspondences. These techniques are demonstrated on both synthetic and real images.