Integrating 3D Slicer with a Dynamic Simulator for Situational Aware Robotic Interventions

Image-guided robotic interventions represent a transformative frontier in surgery, blending advanced imaging and robotics for improved precision and outcomes. This paper addresses the critical need for integrating open-source platforms to enhance situational awareness in image-guided robotic research. We present an open-source toolset that seamlessly combines a physics-based constraint formulation framework, AMBF, with a state-of-the-art imaging platform application, 3D Slicer. Our toolset facilitates the creation of highly customizable interactive digital twins, that incorporates processing and visualization of medical imaging, robot kinematics, and scene dynamics for real-time robot control. Through a feasibility study, we showcase real-time synchronization of a physical robotic interventional environment in both 3D Slicer and AMBF, highlighting low-latency updates and improved visualization.

Condition numbers in multiview geometry, instability in relative pose estimation, and RANSAC

In this paper we introduce a general framework for analyzing the numerical conditioning of minimal problems in multiple view geometry, using tools from computational algebra and Riemannian geometry. Special motivation comes from the fact that relative pose estimation, based on standard 5-point or 7-point Random Sample Consensus (RANSAC) algorithms, can fail even when no outliers are present and there is enough data to support a hypothesis. We argue that these cases arise due to the intrinsic instability of the 5- and 7-point minimal problems. We apply our framework to characterize the instabilities, both in terms of the world scenes that lead to infinite condition number, and directly in terms of ill-conditioned image data. The approach produces computational tests for assessing the condition number before solving the minimal problem. Lastly synthetic and real data experiments suggest that RANSAC serves not only to remove outliers, but also to select for well-conditioned image data, as predicted by our theory.

On the Instability of Relative Pose Estimation and RANSAC's Role

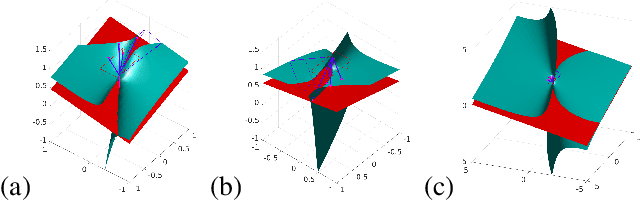
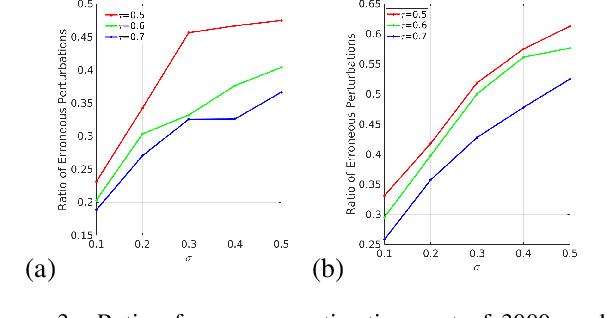
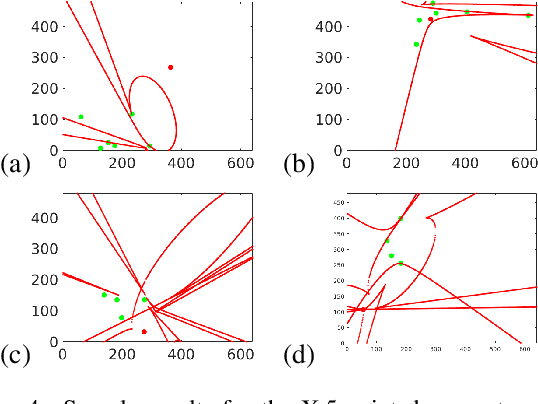
In this paper we study the numerical instabilities of the 5- and 7-point problems for essential and fundamental matrix estimation in multiview geometry. In both cases we characterize the ill-posed world scenes where the condition number for epipolar estimation is infinite. We also characterize the ill-posed instances in terms of the given image data. To arrive at these results, we present a general framework for analyzing the conditioning of minimal problems in multiview geometry, based on Riemannian manifolds. Experiments with synthetic and real-world data then reveal a striking conclusion: that Random Sample Consensus (RANSAC) in Structure-from-Motion (SfM) does not only serve to filter out outliers, but RANSAC also selects for well-conditioned image data, sufficiently separated from the ill-posed locus that our theory predicts. Our findings suggest that, in future work, one could try to accelerate and increase the success of RANSAC by testing only well-conditioned image data.

Benchmarking Pedestrian Odometry: The Brown Pedestrian Odometry Dataset (BPOD)

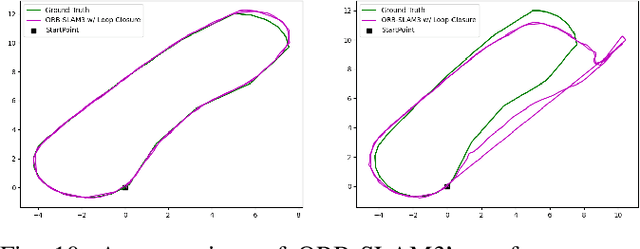
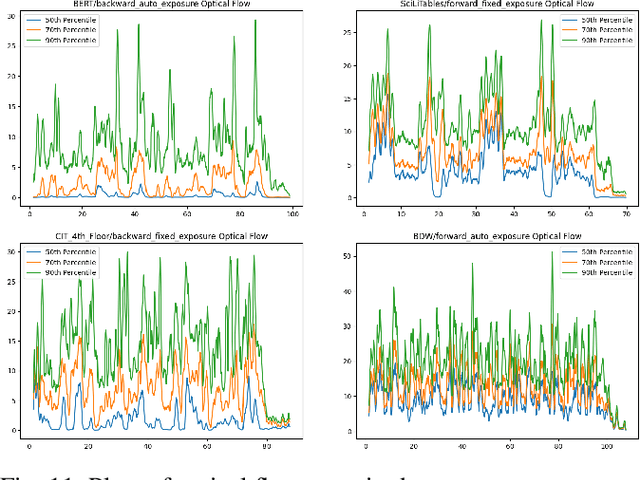
We present the Brown Pedestrian Odometry Dataset (BPOD) for benchmarking visual odometry algorithms in head-mounted pedestrian settings. This dataset was captured using synchronized global and rolling shutter stereo cameras in 12 diverse indoor and outdoor locations on Brown University's campus. Compared to existing datasets, BPOD contains more image blur and self-rotation, which are common in pedestrian odometry but rare elsewhere. Ground-truth trajectories are generated from stick-on markers placed along the pedestrian's path, and the pedestrian's position is documented using a third-person video. We evaluate the performance of representative direct, feature-based, and learning-based VO methods on BPOD. Our results show that significant development is needed to successfully capture pedestrian trajectories. The link to the dataset is here: \url{https://doi.org/10.26300/c1n7-7p93

GPU-Based Homotopy Continuation for Minimal Problems in Computer Vision

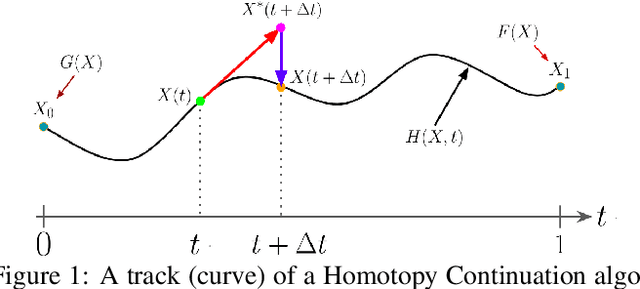
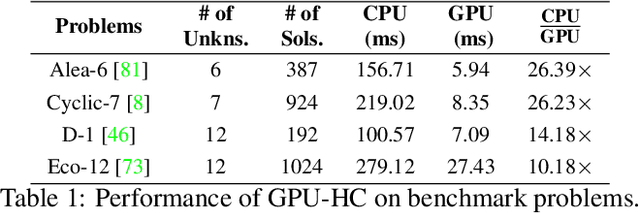
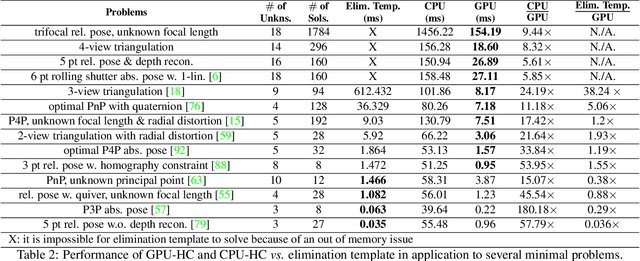
Systems of polynomial equations arise frequently in computer vision, especially in multiview geometry problems. Traditional methods for solving these systems typically aim to eliminate variables to reach a univariate polynomial, e.g., a tenth-order polynomial for 5-point pose estimation, using clever manipulations, or more generally using Grobner basis, resultants, and elimination templates, leading to successful algorithms for multiview geometry and other problems. However, these methods do not work when the problem is complex and when they do, they face efficiency and stability issues. Homotopy Continuation (HC) can solve more complex problems without the stability issues, and with guarantees of a global solution, but they are known to be slow. In this paper we show that HC can be parallelized on a GPU, showing significant speedups up to 26 times on polynomial benchmarks. We also show that GPU-HC can be generically applied to a range of computer vision problems, including 4-view triangulation and trifocal pose estimation with unknown focal length, which cannot be solved with elimination template but they can be efficiently solved with HC. GPU-HC opens the door to easy formulation and solution of a range of computer vision problems.

Trifocal Relative Pose from Lines at Points and its Efficient Solution

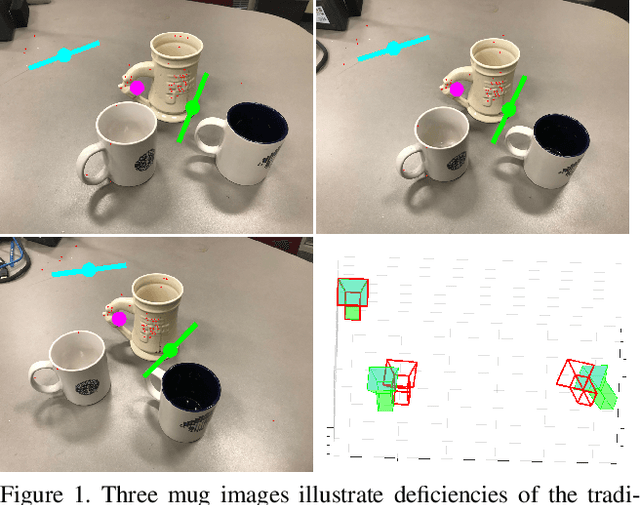
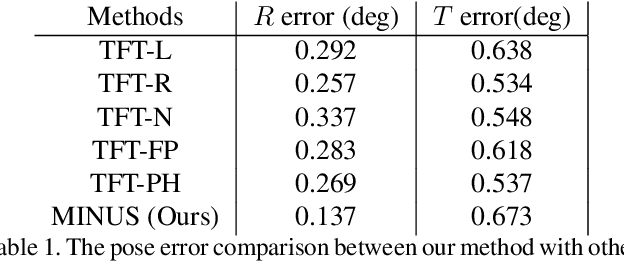
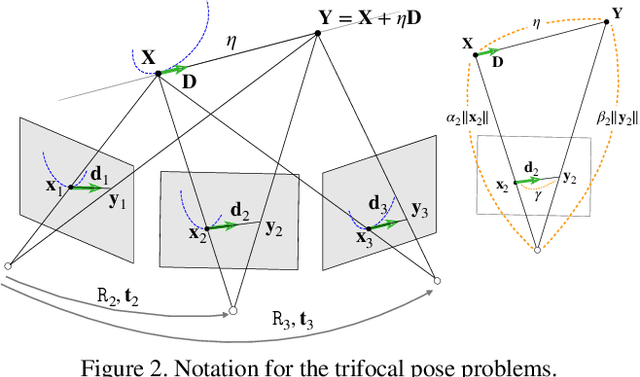
We present a new minimal problem for relative pose estimation mixing point features with lines incident at points observed in three views and its efficient homotopy continuation solver. We demonstrate the generality of the approach by analyzing and solving an additional problem with mixed point and line correspondences in three views. The minimal problems include correspondences of (i) three points and one line and (ii) three points and two lines through two of the points which is reported and analyzed here for the first time. These are difficult to solve, as they have 216 and - as shown here - 312 solutions, but cover important practical situations when line and point features appear together, e.g., in urban scenes or when observing curves. We demonstrate that even such difficult problems can be solved robustly using a suitable homotopy continuation technique and we provide an implementation optimized for minimal problems that can be integrated into engineering applications. Our simulated and real experiments demonstrate our solvers in the camera geometry computation task in structure from motion. We show that new solvers allow for reconstructing challenging scenes where the standard two-view initialization of structure from motion fails.