On the Instability of Relative Pose Estimation and RANSAC's Role
Paper and Code
Dec 29, 2021
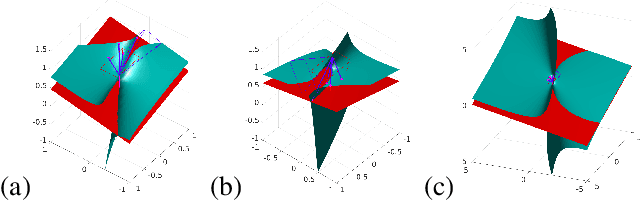
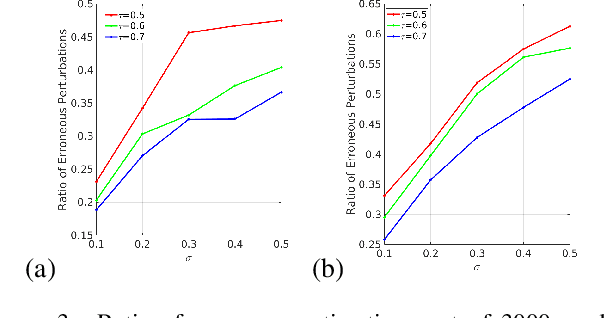
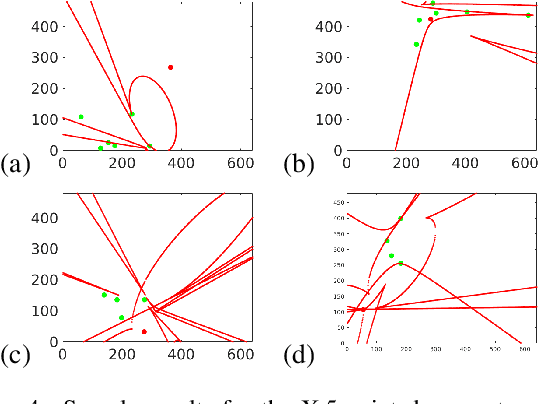
In this paper we study the numerical instabilities of the 5- and 7-point problems for essential and fundamental matrix estimation in multiview geometry. In both cases we characterize the ill-posed world scenes where the condition number for epipolar estimation is infinite. We also characterize the ill-posed instances in terms of the given image data. To arrive at these results, we present a general framework for analyzing the conditioning of minimal problems in multiview geometry, based on Riemannian manifolds. Experiments with synthetic and real-world data then reveal a striking conclusion: that Random Sample Consensus (RANSAC) in Structure-from-Motion (SfM) does not only serve to filter out outliers, but RANSAC also selects for well-conditioned image data, sufficiently separated from the ill-posed locus that our theory predicts. Our findings suggest that, in future work, one could try to accelerate and increase the success of RANSAC by testing only well-conditioned image data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge