GPU-Based Homotopy Continuation for Minimal Problems in Computer Vision

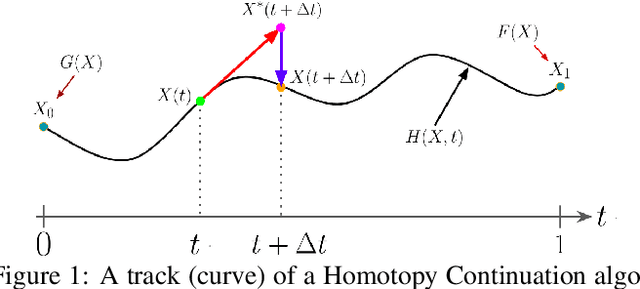
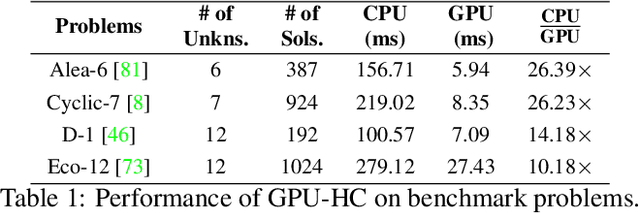
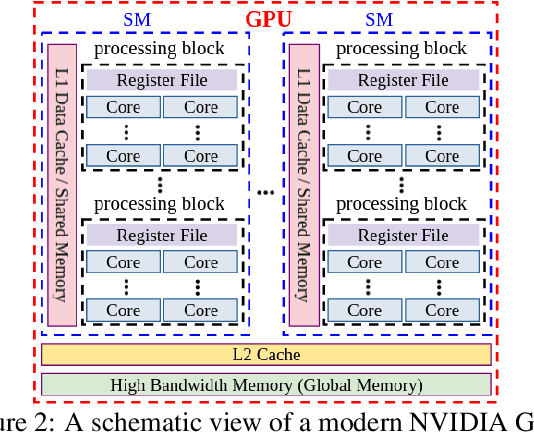
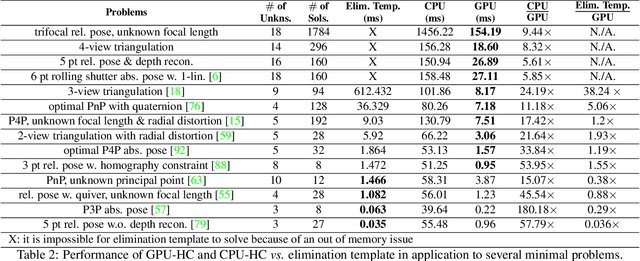
Systems of polynomial equations arise frequently in computer vision, especially in multiview geometry problems. Traditional methods for solving these systems typically aim to eliminate variables to reach a univariate polynomial, e.g., a tenth-order polynomial for 5-point pose estimation, using clever manipulations, or more generally using Grobner basis, resultants, and elimination templates, leading to successful algorithms for multiview geometry and other problems. However, these methods do not work when the problem is complex and when they do, they face efficiency and stability issues. Homotopy Continuation (HC) can solve more complex problems without the stability issues, and with guarantees of a global solution, but they are known to be slow. In this paper we show that HC can be parallelized on a GPU, showing significant speedups up to 26 times on polynomial benchmarks. We also show that GPU-HC can be generically applied to a range of computer vision problems, including 4-view triangulation and trifocal pose estimation with unknown focal length, which cannot be solved with elimination template but they can be efficiently solved with HC. GPU-HC opens the door to easy formulation and solution of a range of computer vision problems.

Truncated Log-concave Sampling with Reflective Hamiltonian Monte Carlo

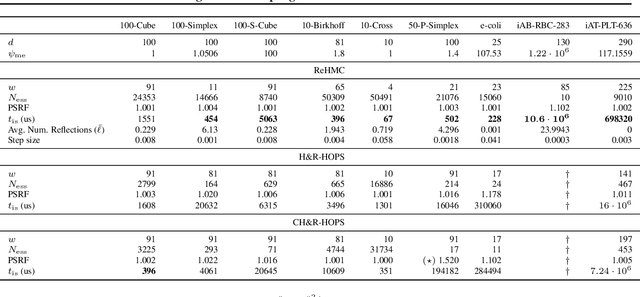
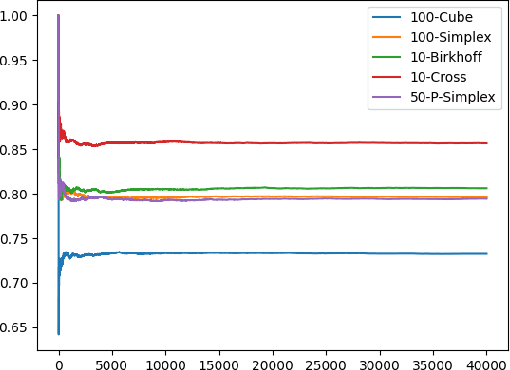
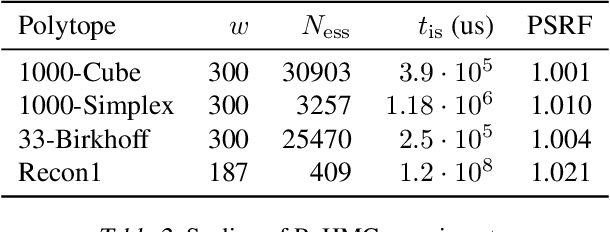
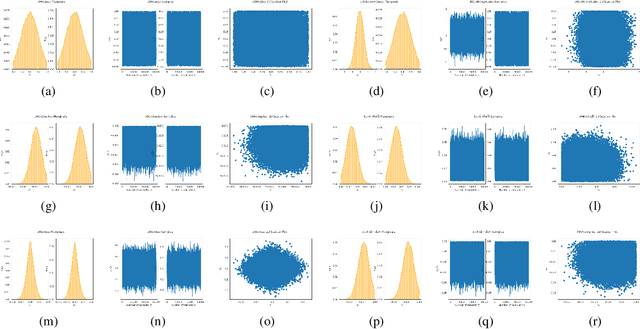
We introduce Reflective Hamiltonian Monte Carlo (ReHMC), an HMC-based algorithm, to sample from a log-concave distribution restricted to a convex polytope. We prove that, starting from a warm start, it mixes in $\widetilde O(\kappa d^2 \ell^2 \log (1 / \varepsilon))$ steps for a well-rounded polytope, ignoring logarithmic factors where $\kappa$ is the condition number of the negative log-density, $d$ is the dimension, $\ell$ is an upper bound on the number of reflections, and $\varepsilon$ is the accuracy parameter. We also developed an open source implementation of ReHMC and we performed an experimental study on various high-dimensional data-sets. Experiments suggest that ReHMC outperfroms Hit-and-Run and Coordinate-Hit-and-Run regarding the time it needs to produce an independent sample.

Trifocal Relative Pose from Lines at Points and its Efficient Solution

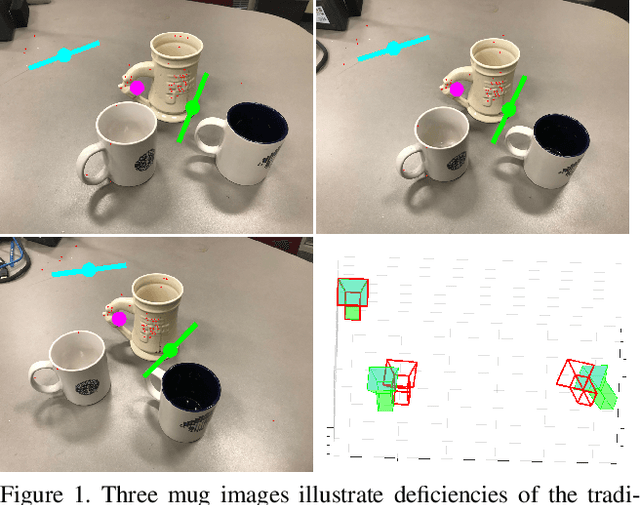
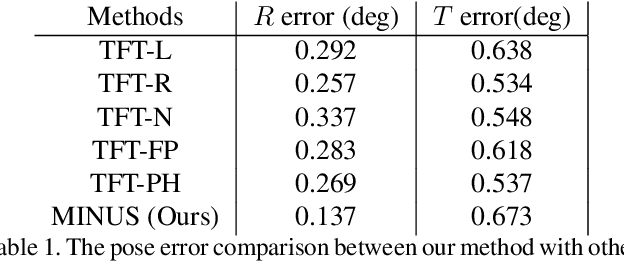
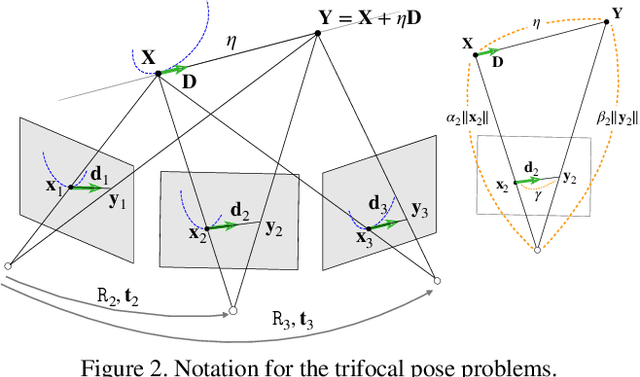
We present a new minimal problem for relative pose estimation mixing point features with lines incident at points observed in three views and its efficient homotopy continuation solver. We demonstrate the generality of the approach by analyzing and solving an additional problem with mixed point and line correspondences in three views. The minimal problems include correspondences of (i) three points and one line and (ii) three points and two lines through two of the points which is reported and analyzed here for the first time. These are difficult to solve, as they have 216 and - as shown here - 312 solutions, but cover important practical situations when line and point features appear together, e.g., in urban scenes or when observing curves. We demonstrate that even such difficult problems can be solved robustly using a suitable homotopy continuation technique and we provide an implementation optimized for minimal problems that can be integrated into engineering applications. Our simulated and real experiments demonstrate our solvers in the camera geometry computation task in structure from motion. We show that new solvers allow for reconstructing challenging scenes where the standard two-view initialization of structure from motion fails.

Characterizing and approximating eigenvalue sets of symmetric interval matrices

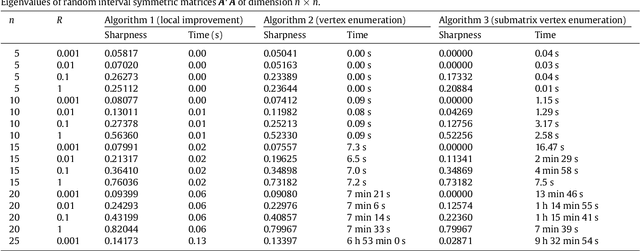
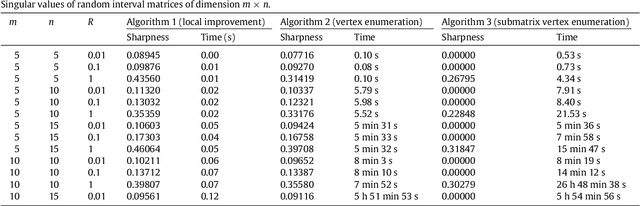
We consider the eigenvalue problem for the case where the input matrix is symmetric and its entries perturb in some given intervals. We present a characterization of some of the exact boundary points, which allows us to introduce an inner approximation algorithm, that in many case estimates exact bounds. To our knowledge, this is the first algorithm that is able to guaran- tee exactness. We illustrate our approach by several examples and numerical experiments.