Vissarion Fisikopoulos
Truncated Log-concave Sampling with Reflective Hamiltonian Monte Carlo
Feb 25, 2021
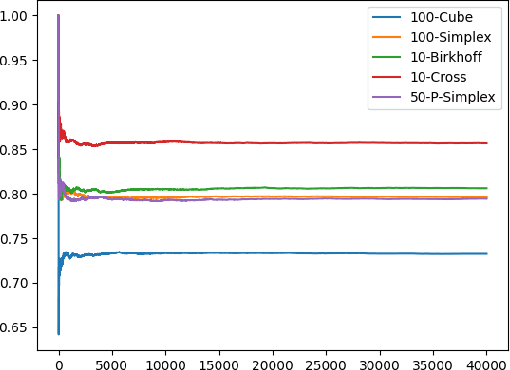
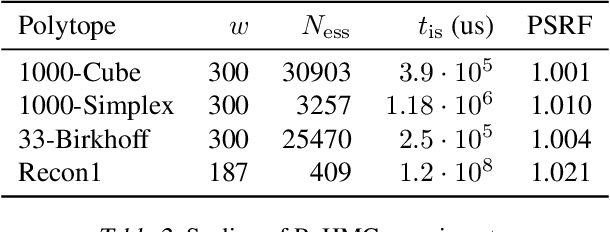
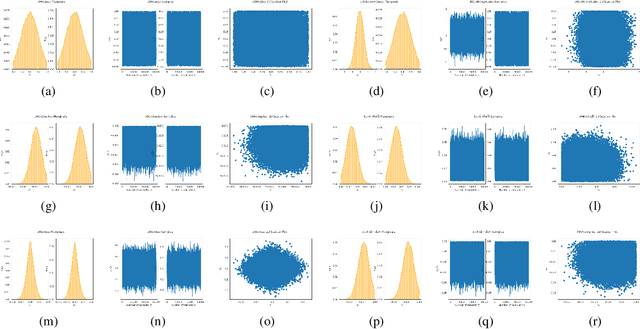
Abstract:We introduce Reflective Hamiltonian Monte Carlo (ReHMC), an HMC-based algorithm, to sample from a log-concave distribution restricted to a convex polytope. We prove that, starting from a warm start, it mixes in $\widetilde O(\kappa d^2 \ell^2 \log (1 / \varepsilon))$ steps for a well-rounded polytope, ignoring logarithmic factors where $\kappa$ is the condition number of the negative log-density, $d$ is the dimension, $\ell$ is an upper bound on the number of reflections, and $\varepsilon$ is the accuracy parameter. We also developed an open source implementation of ReHMC and we performed an experimental study on various high-dimensional data-sets. Experiments suggest that ReHMC outperfroms Hit-and-Run and Coordinate-Hit-and-Run regarding the time it needs to produce an independent sample.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge