Simulation Study of the Upper-limb Wrench Feasible Set with Glenohumeral Joint Constraints

The aim of this work is to improve musculoskeletal-based models of the upper-limb Wrench Feasible Set i.e. the set of achievable maximal wrenches at the hand for applications in collaborative robotics and computer aided ergonomics. In particular, a recent method performing wrench capacity evaluation called the Iterative Convex Hull Method is upgraded in order to integrate non dislocation and compression limitation constraints at the glenohumeral joint not taken into account in the available models. Their effects on the amplitude of the force capacities at the hand, glenohumeral joint reaction forces and upper-limb muscles coordination in comparison to the original iterative convex hull method are investigated in silico. The results highlight the glenohumeral potential dislocation for the majority of elements of the wrench feasible set with the original Iterative Convex Hull method and the fact that the modifications satisfy correctly stability constraints at the glenohumeral joint. Also, the induced muscles coordination pattern favors the action of stabilizing muscles, in particular the rotator-cuff muscles, and lowers that of known potential destabilizing ones according to the literature.

On-line feasible wrench polytope evaluation based on human musculoskeletal models: an iterative convex hull method

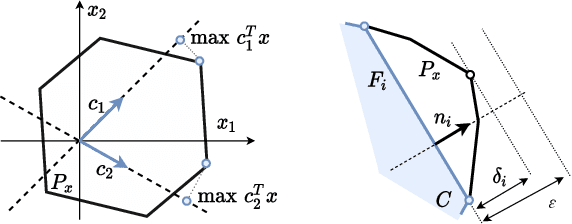
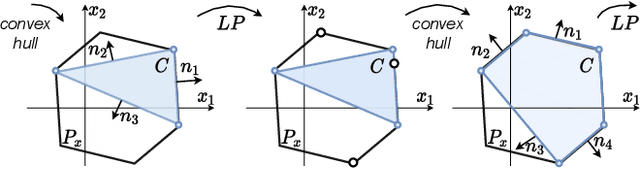
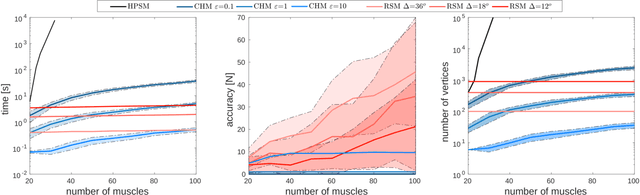
Many recent human-robot collaboration strategies, such as Assist-As-Needed (AAN), are promoting humancentered robot control, where the robot continuously adapts its assistance level based on the real-time need of its human counterpart. One of the fundamental assumptions of these approaches is the ability to measure or estimate the physical capacity of humans in real-time. In this work, we propose an algorithm for the feasibility set analysis of a generic class of linear algebra problems. This novel iterative convex-hull method is applied to the determination of the feasible Cartesian wrench polytope associated to a musculoskeletal model of the human upper limb. The method is capable of running in real-time and allows the user to define the desired estimation accuracy. The algorithm performance analysis shows that the execution time has near-linear relationship to the considered number of muscles, as opposed to the exponential relationship of the conventional methods. Finally, real-time robot control application of the algorithm is demonstrated in a Collaborative carrying experiment, where a human operator and a Franka Emika Panda robot jointly carry a 7kg object. The robot is controlled in accordance to the AAN paradigm maintaining the load carried by the human operator at 30% of its carrying capacity.

Efficient Set-Based Approaches for the Reliable Computation of Robot Capabilities

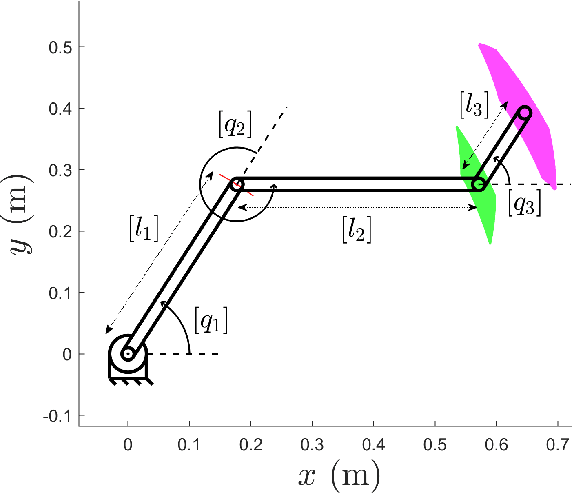
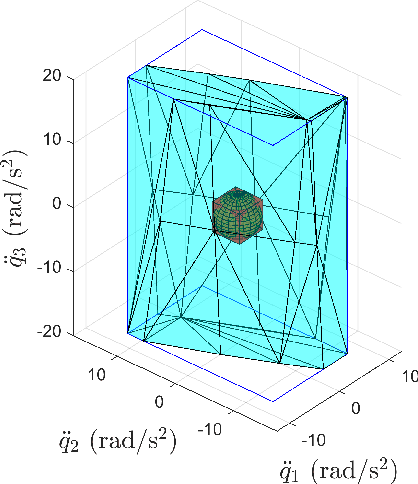
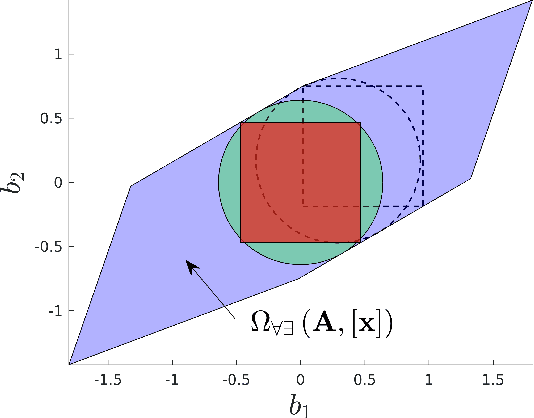
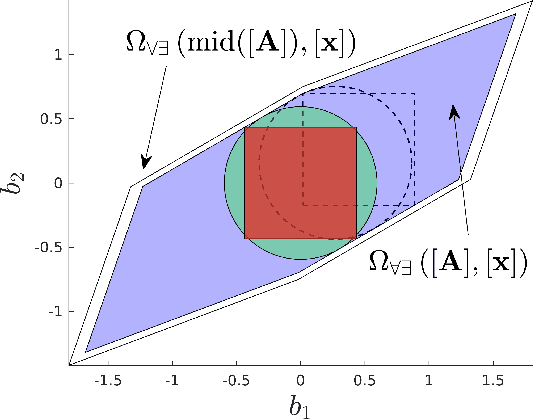
To reliably model real robot characteristics, interval linear systems of equations allow to describe families of problems that consider sets of values. This allows to easily account for typical complexities such as sets of joint states and design parameter uncertainties. Inner approximations of the solutions to the interval linear systems can be used to describe the common capabilities of a robotic manipulator corresponding to the considered sets of values. In this work, several classes of problems are considered. For each class, reliable and efficient polytope, n-cube, and n-ball inner approximations are presented. The interval approaches usually proposed are inefficient because they are too computationally heavy for certain applications, such as control. We propose efficient new inner approximation theorems for the considered classes of problems. This allows for usage with real-time applications as well as rapid analysis of potential designs. Several applications are presented for a redundant planar manipulator including locally evaluating the manipulator's velocity, acceleration, and static force capabilities, and evaluating its future acceleration capabilities over a given time horizon.

On-line force capability evaluation based on efficient polytope vertex search

Ellipsoid-based manipulability measures are often used to characterize the force/velocity task-space capabilities of robots. While computationally simple, this approach largely approximate and underestimate the true capabilities. Force/velocity polytopes appear to be a more appropriate representation to characterize robot's task-space capabilities. However, due to the computational complexity of the associated vertex search problem, the polytope approach is mostly restricted to offline use, e.g. as a tool aiding robot mechanical design, robot placement in work-space and offline trajectory planning. In this paper, a novel on-line polytope vertex search algorithm is proposed. It exploits the parallelotop geometry of actuator constraints. The proposed algorithm significantly reduces the complexity and computation time of the vertex search problem in comparison to commonly used algorithms. In order to highlight the on-line capability of the proposed algorithm and its potential for robot control, a challenging experiment with two collaborating Franka Emika Panda robots, carrying a load of 12 kilograms, is proposed. In this experiment, the load distribution is adapted on-line, as a function of the configuration dependant task-space force capability of each robot, in order to avoid, as much as possible, the saturation of their capacity.

Characterizing and approximating eigenvalue sets of symmetric interval matrices

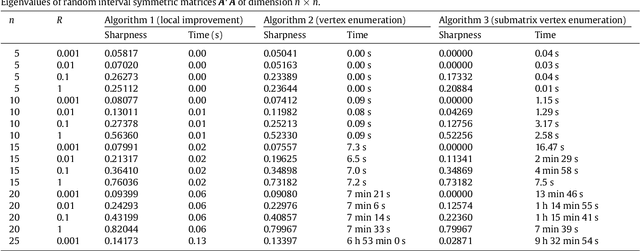
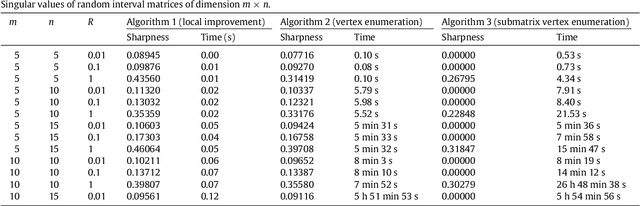
We consider the eigenvalue problem for the case where the input matrix is symmetric and its entries perturb in some given intervals. We present a characterization of some of the exact boundary points, which allows us to introduce an inner approximation algorithm, that in many case estimates exact bounds. To our knowledge, this is the first algorithm that is able to guaran- tee exactness. We illustrate our approach by several examples and numerical experiments.