Efficient Set-Based Approaches for the Reliable Computation of Robot Capabilities
Paper and Code
Apr 01, 2021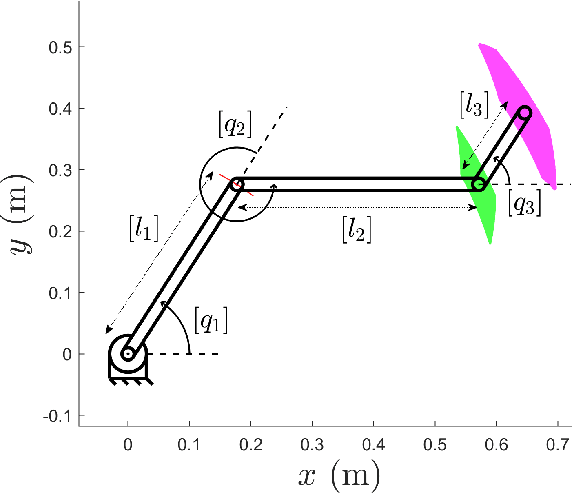
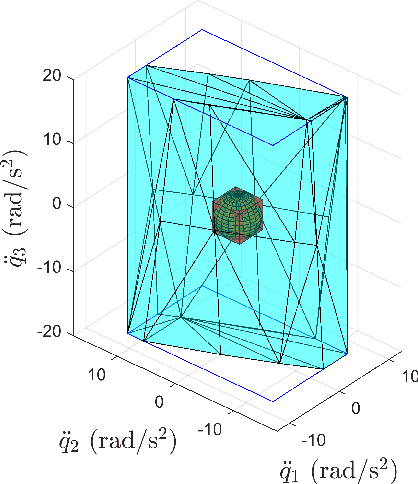
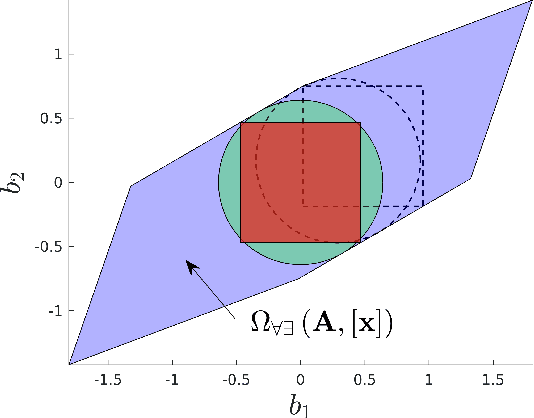
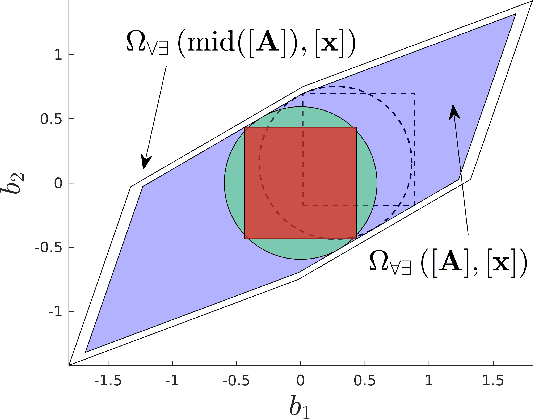
To reliably model real robot characteristics, interval linear systems of equations allow to describe families of problems that consider sets of values. This allows to easily account for typical complexities such as sets of joint states and design parameter uncertainties. Inner approximations of the solutions to the interval linear systems can be used to describe the common capabilities of a robotic manipulator corresponding to the considered sets of values. In this work, several classes of problems are considered. For each class, reliable and efficient polytope, n-cube, and n-ball inner approximations are presented. The interval approaches usually proposed are inefficient because they are too computationally heavy for certain applications, such as control. We propose efficient new inner approximation theorems for the considered classes of problems. This allows for usage with real-time applications as well as rapid analysis of potential designs. Several applications are presented for a redundant planar manipulator including locally evaluating the manipulator's velocity, acceleration, and static force capabilities, and evaluating its future acceleration capabilities over a given time horizon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge