Milan Hladík
AUCTUS, IMS
Kernel-Free Universum Quadratic Surface Twin Support Vector Machines for Imbalanced Data
Dec 02, 2024
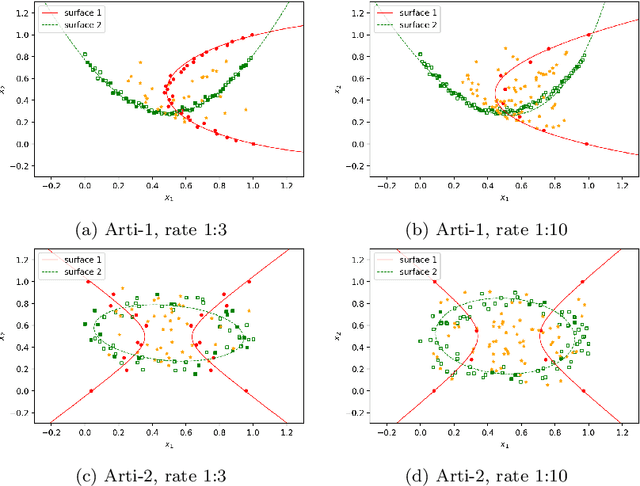
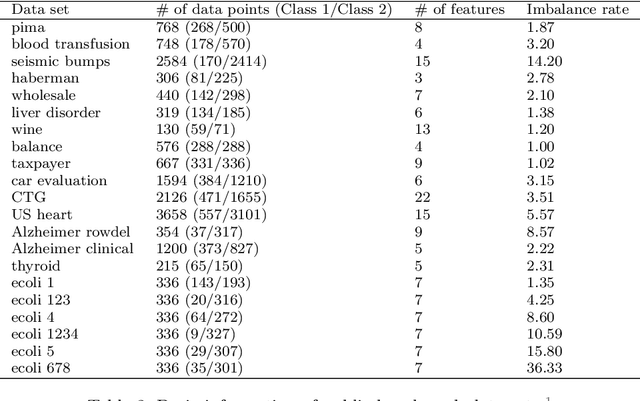
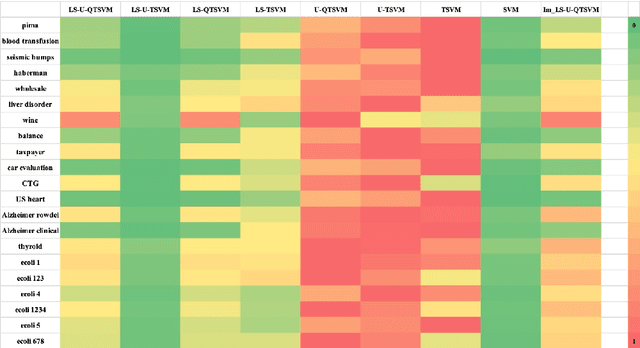
Abstract:Binary classification tasks with imbalanced classes pose significant challenges in machine learning. Traditional classifiers often struggle to accurately capture the characteristics of the minority class, resulting in biased models with subpar predictive performance. In this paper, we introduce a novel approach to tackle this issue by leveraging Universum points to support the minority class within quadratic twin support vector machine models. Unlike traditional classifiers, our models utilize quadratic surfaces instead of hyperplanes for binary classification, providing greater flexibility in modeling complex decision boundaries. By incorporating Universum points, our approach enhances classification accuracy and generalization performance on imbalanced datasets. We generated four artificial datasets to demonstrate the flexibility of the proposed methods. Additionally, we validated the effectiveness of our approach through empirical evaluations on benchmark datasets, showing superior performance compared to conventional classifiers and existing methods for imbalanced classification.
Multi-task twin support vector machine with Universum data
Jun 22, 2022

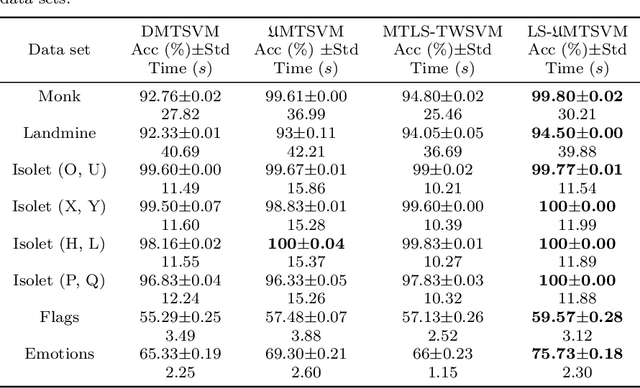

Abstract:Multi-task learning (MTL) has emerged as a promising topic of machine learning in recent years, aiming to enhance the performance of numerous related learning tasks by exploiting beneficial information. During the training phase, most of the existing multi-task learning models concentrate entirely on the target task data and ignore the non-target task data contained in the target tasks. To address this issue, Universum data, that do not correspond to any class of a classification problem, may be used as prior knowledge in the training model. This study looks at the challenge of multi-task learning using Universum data to employ non-target task data, which leads to better performance. It proposes a multi-task twin support vector machine with Universum data (UMTSVM) and provides two approaches to its solution. The first approach takes into account the dual formulation of UMTSVM and tries to solve a quadratic programming problem. The second approach formulates a least-squares version of UMTSVM and refers to it as LS-UMTSVM to further increase the generalization performance. The solution of the two primal problems in LS-UMTSVM is simplified to solving just two systems of linear equations, resulting in an incredibly simple and quick approach. Numerical experiments on several popular multi-task data sets and medical data sets demonstrate the efficiency of the proposed methods.
Sparse Universum Quadratic Surface Support Vector Machine Models for Binary Classification
Apr 03, 2021

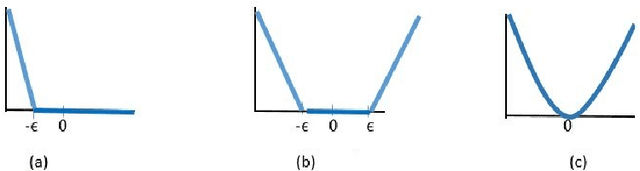

Abstract:In binary classification, kernel-free linear or quadratic support vector machines are proposed to avoid dealing with difficulties such as finding appropriate kernel functions or tuning their hyper-parameters. Furthermore, Universum data points, which do not belong to any class, can be exploited to embed prior knowledge into the corresponding models so that the generalization performance is improved. In this paper, we design novel kernel-free Universum quadratic surface support vector machine models. Further, we propose the L1 norm regularized version that is beneficial for detecting potential sparsity patterns in the Hessian of the quadratic surface and reducing to the standard linear models if the data points are (almost) linearly separable. The proposed models are convex such that standard numerical solvers can be utilized for solving them. Nonetheless, we formulate a least squares version of the L1 norm regularized model and next, design an effective tailored algorithm that only requires solving one linear system. Several theoretical properties of these models are then reported/proved as well. We finally conduct numerical experiments on both artificial and public benchmark data sets to demonstrate the feasibility and effectiveness of the proposed models.
Efficient Set-Based Approaches for the Reliable Computation of Robot Capabilities
Apr 01, 2021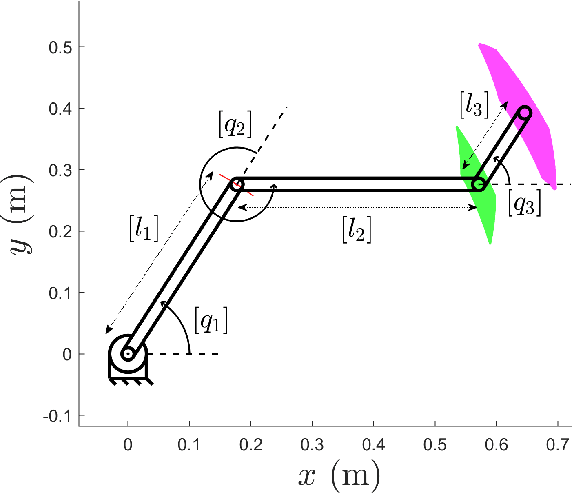
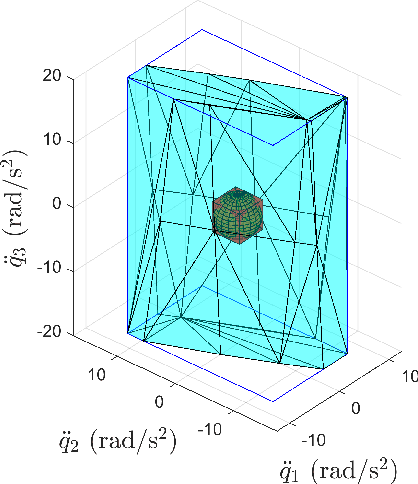
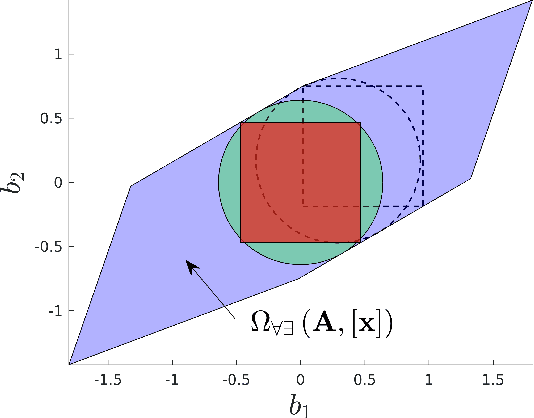
Abstract:To reliably model real robot characteristics, interval linear systems of equations allow to describe families of problems that consider sets of values. This allows to easily account for typical complexities such as sets of joint states and design parameter uncertainties. Inner approximations of the solutions to the interval linear systems can be used to describe the common capabilities of a robotic manipulator corresponding to the considered sets of values. In this work, several classes of problems are considered. For each class, reliable and efficient polytope, n-cube, and n-ball inner approximations are presented. The interval approaches usually proposed are inefficient because they are too computationally heavy for certain applications, such as control. We propose efficient new inner approximation theorems for the considered classes of problems. This allows for usage with real-time applications as well as rapid analysis of potential designs. Several applications are presented for a redundant planar manipulator including locally evaluating the manipulator's velocity, acceleration, and static force capabilities, and evaluating its future acceleration capabilities over a given time horizon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge