Sparse L0-norm based Kernel-free Quadratic Surface Support Vector Machines

Kernel-free quadratic surface support vector machine (SVM) models have gained significant attention in machine learning. However, introducing a quadratic classifier increases the model's complexity by quadratically expanding the number of parameters relative to the dimensionality of the data, exacerbating overfitting. To address this, we propose sparse $\ell_0$-norm based Kernel-free quadratic surface SVMs, designed to mitigate overfitting and enhance interpretability. Given the intractable nature of these models, we present a penalty decomposition algorithm to efficiently obtain first-order optimality points. Our analysis shows that the subproblems in this framework either admit closed-form solutions or can leverage duality theory to improve computational efficiency. Through empirical evaluations on real-world datasets, we demonstrate the efficacy and robustness of our approach, showcasing its potential to advance Kernel-free quadratic surface SVMs in practical applications while addressing overfitting concerns. All the implemented models and experiment codes are available at \url{https://github.com/raminzandvakili/L0-QSVM}.

Kernel-Free Universum Quadratic Surface Twin Support Vector Machines for Imbalanced Data

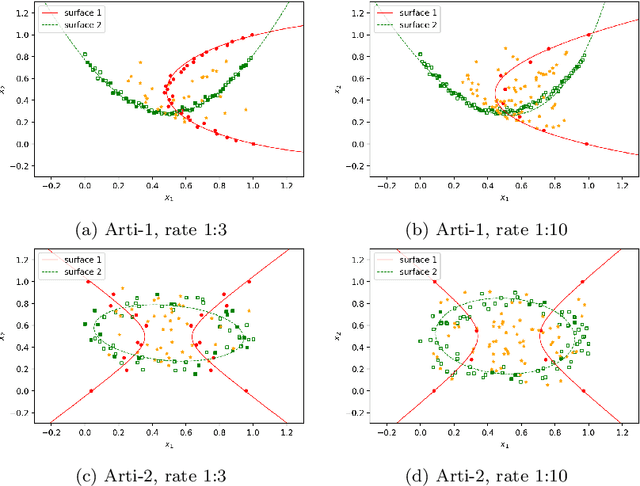
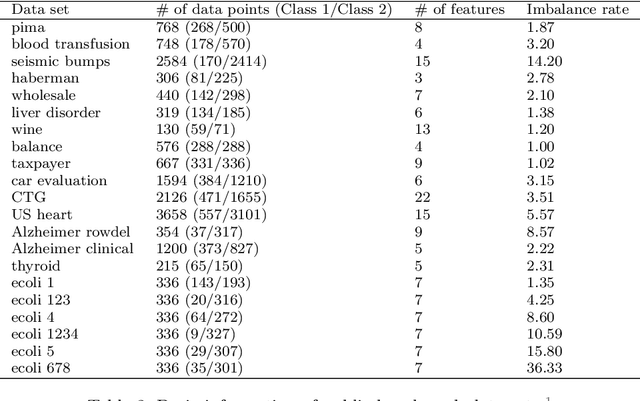
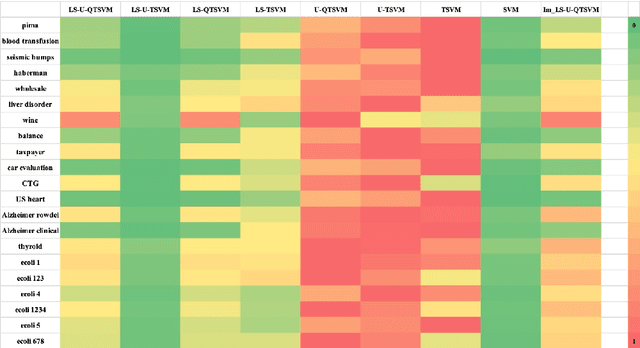
Binary classification tasks with imbalanced classes pose significant challenges in machine learning. Traditional classifiers often struggle to accurately capture the characteristics of the minority class, resulting in biased models with subpar predictive performance. In this paper, we introduce a novel approach to tackle this issue by leveraging Universum points to support the minority class within quadratic twin support vector machine models. Unlike traditional classifiers, our models utilize quadratic surfaces instead of hyperplanes for binary classification, providing greater flexibility in modeling complex decision boundaries. By incorporating Universum points, our approach enhances classification accuracy and generalization performance on imbalanced datasets. We generated four artificial datasets to demonstrate the flexibility of the proposed methods. Additionally, we validated the effectiveness of our approach through empirical evaluations on benchmark datasets, showing superior performance compared to conventional classifiers and existing methods for imbalanced classification.

Enigma: Privacy-Preserving Execution of QAOA on Untrusted Quantum Computers

Quantum computers can solve problems that are beyond the capabilities of conventional computers. As quantum computers are expensive and hard to maintain, the typical model for performing quantum computation is to send the circuit to a quantum cloud provider. This leads to privacy concerns for commercial entities as an untrusted server can learn protected information from the provided circuit. Current proposals for Secure Quantum Computing (SQC) either rely on emerging technologies (such as quantum networks) or incur prohibitive overheads (for Quantum Homomorphic Encryption). The goal of our paper is to enable low-cost privacy-preserving quantum computation that can be used with current systems. We propose Enigma, a suite of privacy-preserving schemes specifically designed for the Quantum Approximate Optimization Algorithm (QAOA). Unlike previous SQC techniques that obfuscate quantum circuits, Enigma transforms the input problem of QAOA, such that the resulting circuit and the outcomes are unintelligible to the server. We introduce three variants of Enigma. Enigma-I protects the coefficients of QAOA using random phase flipping and fudging of values. Enigma-II protects the nodes of the graph by introducing decoy qubits, which are indistinguishable from primary ones. Enigma-III protects the edge information of the graph by modifying the graph such that each node has an identical number of connections. For all variants of Enigma, we demonstrate that we can still obtain the solution for the original problem. We evaluate Enigma using IBM quantum devices and show that the privacy improvements of Enigma come at only a small reduction in fidelity (1%-13%).

A Penalty Based Method for Communication-Efficient Decentralized Bilevel Programming

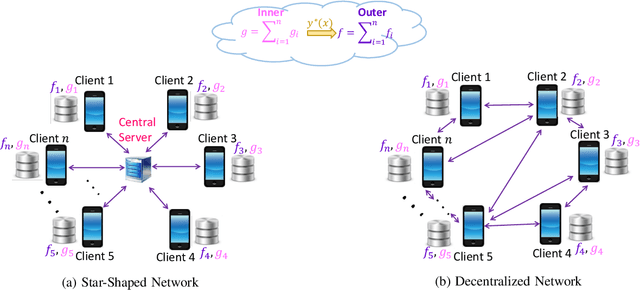
Bilevel programming has recently received attention in the literature, due to a wide range of applications, including reinforcement learning and hyper-parameter optimization. However, it is widely assumed that the underlying bilevel optimization problem is solved either by a single machine or in the case of multiple machines connected in a star-shaped network, i.e., federated learning setting. The latter approach suffers from a high communication cost on the central node (e.g., parameter server) and exhibits privacy vulnerabilities. Hence, it is of interest to develop methods that solve bilevel optimization problems in a communication-efficient decentralized manner. To that end, this paper introduces a penalty function based decentralized algorithm with theoretical guarantees for this class of optimization problems. Specifically, a distributed alternating gradient-type algorithm for solving consensus bilevel programming over a decentralized network is developed. A key feature of the proposed algorithm is to estimate the hyper-gradient of the penalty function via decentralized computation of matrix-vector products and few vector communications, which is then integrated within our alternating algorithm to give the finite-time convergence analysis under different convexity assumptions. Owing to the generality of this complexity analysis, our result yields convergence rates for a wide variety of consensus problems including minimax and compositional optimization. Empirical results on both synthetic and real datasets demonstrate that the proposed method works well in practice.

Sparse Universum Quadratic Surface Support Vector Machine Models for Binary Classification

In binary classification, kernel-free linear or quadratic support vector machines are proposed to avoid dealing with difficulties such as finding appropriate kernel functions or tuning their hyper-parameters. Furthermore, Universum data points, which do not belong to any class, can be exploited to embed prior knowledge into the corresponding models so that the generalization performance is improved. In this paper, we design novel kernel-free Universum quadratic surface support vector machine models. Further, we propose the L1 norm regularized version that is beneficial for detecting potential sparsity patterns in the Hessian of the quadratic surface and reducing to the standard linear models if the data points are (almost) linearly separable. The proposed models are convex such that standard numerical solvers can be utilized for solving them. Nonetheless, we formulate a least squares version of the L1 norm regularized model and next, design an effective tailored algorithm that only requires solving one linear system. Several theoretical properties of these models are then reported/proved as well. We finally conduct numerical experiments on both artificial and public benchmark data sets to demonstrate the feasibility and effectiveness of the proposed models.

Density Estimation using Entropy Maximization for Semi-continuous Data

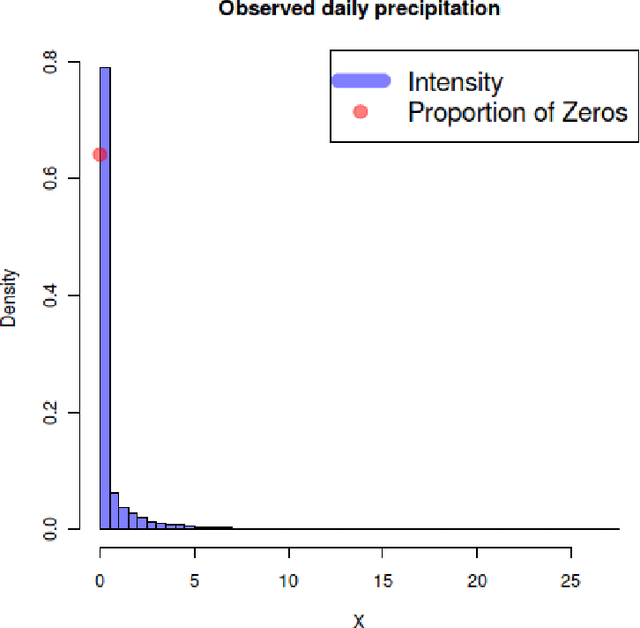
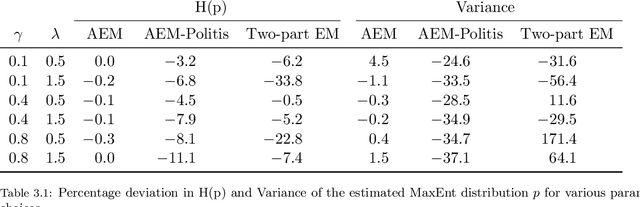
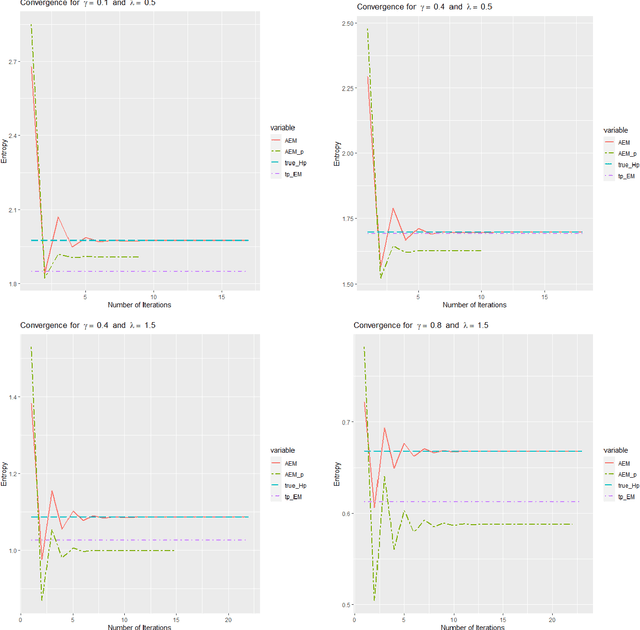
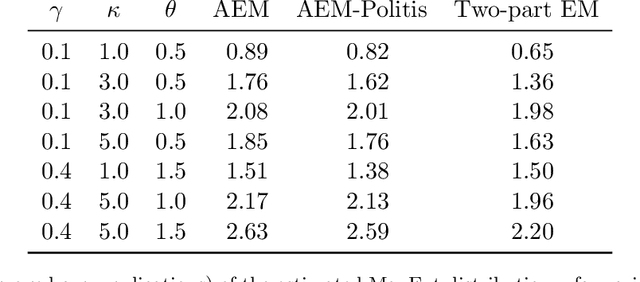
Semi-continuous data comes from a distribution that is a mixture of the point mass at zero and a continuous distribution with support on the positive real line. A clear example is the daily rainfall data. In this paper, we present a novel algorithm to estimate the density function for semi-continuous data using the principle of maximum entropy. Unlike existing methods in the literature, our algorithm needs only the sample values of the constraint functions in the entropy maximization problem and does not need the entire sample. Using simulations, we show that the estimate of the entropy produced by our algorithm has significantly less bias compared to existing methods. An application to the daily rainfall data is provided.