Skipper: Improving the Reach and Fidelity of Quantum Annealers by Skipping Long Chains

Quantum Annealers (QAs) operate as single-instruction machines, lacking a SWAP operation to overcome limited qubit connectivity. Consequently, multiple physical qubits are chained to form a program qubit with higher connectivity, resulting in a drastically diminished effective QA capacity by up to 33x. We observe that in QAs: (a) chain lengths exhibit a power-law distribution, a few dominant chains holding substantially more qubits than others; and (b) about 25% of physical qubits remain unused, getting isolated between these chains. We propose Skipper, a software technique that enhances the capacity and fidelity of QAs by skipping dominant chains and substituting their program qubit with two readout results. Using a 5761-qubit QA, we demonstrate that Skipper can tackle up to 59% (Avg. 28%) larger problems when eleven chains are skipped. Additionally, Skipper can improve QA fidelity by up to 44% (Avg. 33%) when cutting five chains (32 runs). Users can specify up to eleven chain cuts in Skipper, necessitating about 2,000 distinct quantum executable runs. To mitigate this, we introduce Skipper-G, a greedy scheme that skips sub-problems less likely to hold the global optimum, executing a maximum of 23 quantum executables with eleven chain trims. Skipper-G can boost QA fidelity by up to 41% (Avg. 29%) when cutting five chains (11 runs).

Enigma: Privacy-Preserving Execution of QAOA on Untrusted Quantum Computers

Quantum computers can solve problems that are beyond the capabilities of conventional computers. As quantum computers are expensive and hard to maintain, the typical model for performing quantum computation is to send the circuit to a quantum cloud provider. This leads to privacy concerns for commercial entities as an untrusted server can learn protected information from the provided circuit. Current proposals for Secure Quantum Computing (SQC) either rely on emerging technologies (such as quantum networks) or incur prohibitive overheads (for Quantum Homomorphic Encryption). The goal of our paper is to enable low-cost privacy-preserving quantum computation that can be used with current systems. We propose Enigma, a suite of privacy-preserving schemes specifically designed for the Quantum Approximate Optimization Algorithm (QAOA). Unlike previous SQC techniques that obfuscate quantum circuits, Enigma transforms the input problem of QAOA, such that the resulting circuit and the outcomes are unintelligible to the server. We introduce three variants of Enigma. Enigma-I protects the coefficients of QAOA using random phase flipping and fudging of values. Enigma-II protects the nodes of the graph by introducing decoy qubits, which are indistinguishable from primary ones. Enigma-III protects the edge information of the graph by modifying the graph such that each node has an identical number of connections. For all variants of Enigma, we demonstrate that we can still obtain the solution for the original problem. We evaluate Enigma using IBM quantum devices and show that the privacy improvements of Enigma come at only a small reduction in fidelity (1%-13%).

FrozenQubits: Boosting Fidelity of QAOA by Skipping Hotspot Nodes

Quantum Approximate Optimization Algorithm (QAOA) is one of the leading candidates for demonstrating the quantum advantage using near-term quantum computers. Unfortunately, high device error rates limit us from reliably running QAOA circuits for problems with more than a few qubits. In QAOA, the problem graph is translated into a quantum circuit such that every edge corresponds to two 2-qubit CNOT operations in each layer of the circuit. As CNOTs are extremely error-prone, the fidelity of QAOA circuits is dictated by the number of edges in the problem graph. We observe that majority of graphs corresponding to real-world applications follow the ``power-law`` distribution, where some hotspot nodes have significantly higher number of connections. We leverage this insight and propose ``FrozenQubits`` that freezes the hotspot nodes or qubits and intelligently partitions the state-space of the given problem into several smaller sub-spaces which are then solved independently. The corresponding QAOA sub-circuits are significantly less vulnerable to gate and decoherence errors due to the reduced number of CNOT operations in each sub-circuit. Unlike prior circuit-cutting approaches, FrozenQubits does not require any exponentially complex post-processing step. Our evaluations with 5,300 QAOA circuits on eight different quantum computers from IBM shows that FrozenQubits can improve the quality of solutions by 8.73x on average (and by up to 57x), albeit utilizing 2x more quantum resources.

An Ensemble Approach for Compressive Sensing with Quantum

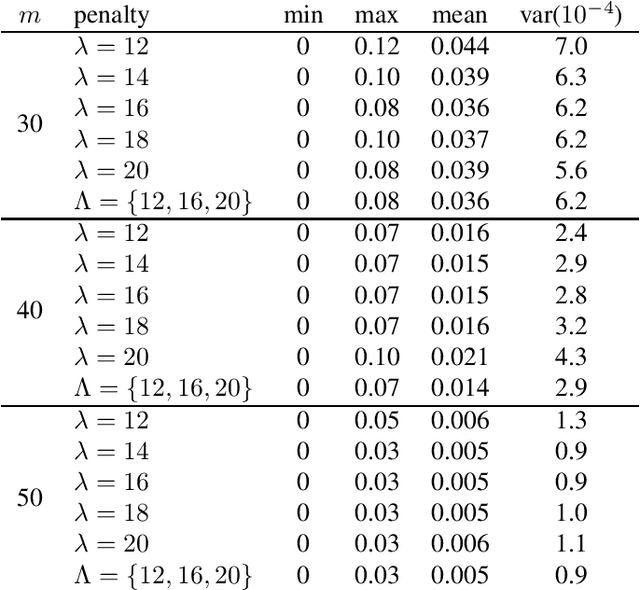
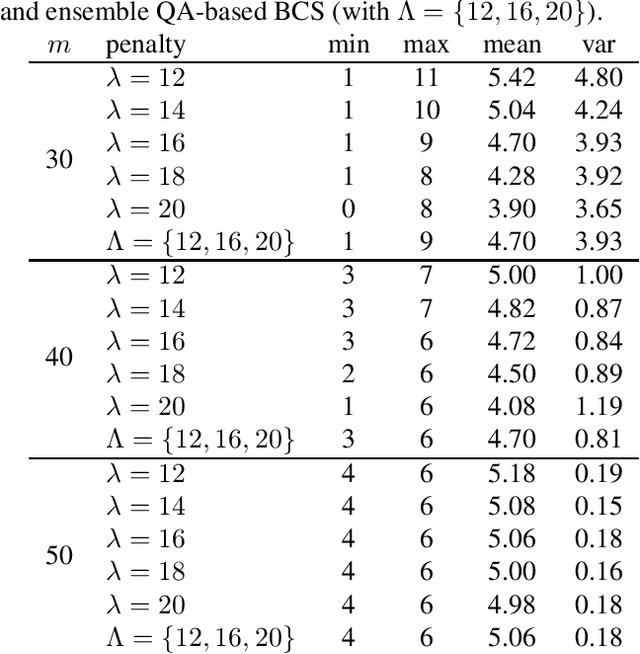
We leverage the idea of a statistical ensemble to improve the quality of quantum annealing based binary compressive sensing. Since executing quantum machine instructions on a quantum annealer can result in an excited state, rather than the ground state of the given Hamiltonian, we use different penalty parameters to generate multiple distinct quadratic unconstrained binary optimization (QUBO) functions whose ground state(s) represent a potential solution of the original problem. We then employ the attained samples from minimizing all corresponding (different) QUBOs to estimate the solution of the problem of binary compressive sensing. Our experiments, on a D-Wave 2000Q quantum processor, demonstrated that the proposed ensemble scheme is notably less sensitive to the calibration of the penalty parameter that controls the trade-off between the feasibility and sparsity of recoveries.

Reinforcement Quantum Annealing: A Quantum-Assisted Learning Automata Approach

We introduce the reinforcement quantum annealing (RQA) scheme in which an intelligent agent interacts with a quantum annealer that plays the stochastic environment role of learning automata and tries to iteratively find better Ising Hamiltonians for the given problem of interest. As a proof-of-concept, we propose a novel approach for reducing the NP-complete problem of Boolean satisfiability (SAT) to minimizing Ising Hamiltonians and show how to apply the RQA for increasing the probability of finding the global optimum. Our experimental results on two different benchmark SAT problems (namely factoring pseudo-prime numbers and random SAT with phase transitions), using a D-Wave 2000Q quantum processor, demonstrated that RQA finds notably better solutions with fewer samples, compared to state-of-the-art techniques in the realm of quantum annealing.