Density Estimation using Entropy Maximization for Semi-continuous Data
Paper and Code
Nov 17, 2020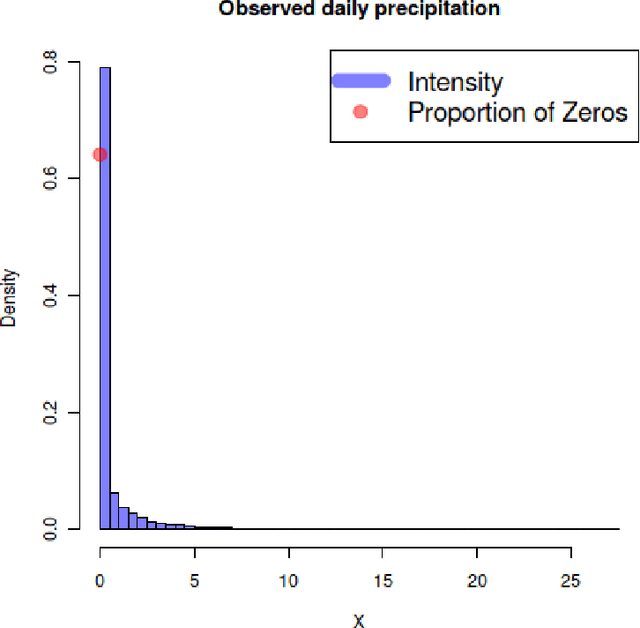
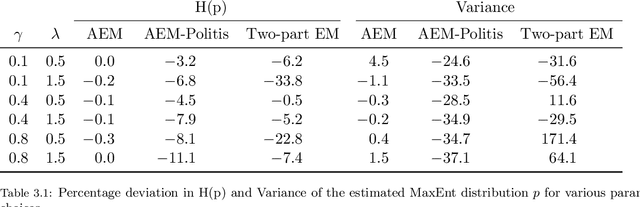
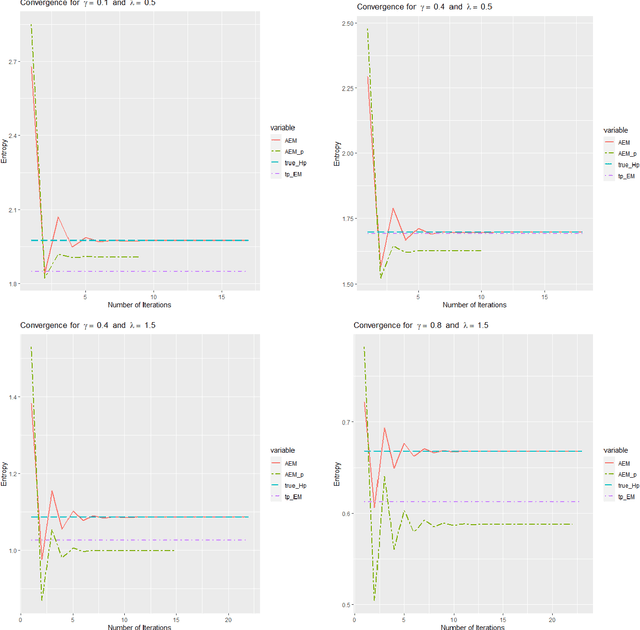
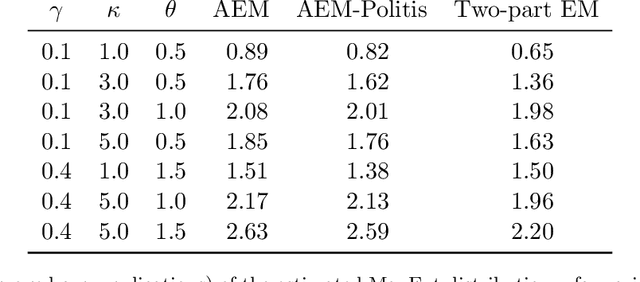
Semi-continuous data comes from a distribution that is a mixture of the point mass at zero and a continuous distribution with support on the positive real line. A clear example is the daily rainfall data. In this paper, we present a novel algorithm to estimate the density function for semi-continuous data using the principle of maximum entropy. Unlike existing methods in the literature, our algorithm needs only the sample values of the constraint functions in the entropy maximization problem and does not need the entire sample. Using simulations, we show that the estimate of the entropy produced by our algorithm has significantly less bias compared to existing methods. An application to the daily rainfall data is provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge