Kernel-Free Universum Quadratic Surface Twin Support Vector Machines for Imbalanced Data

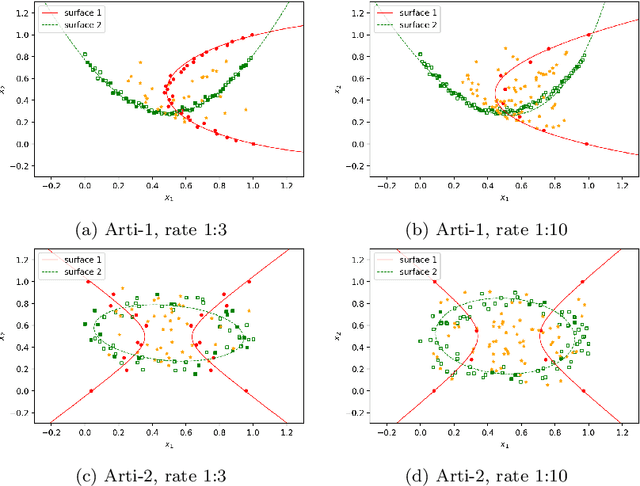
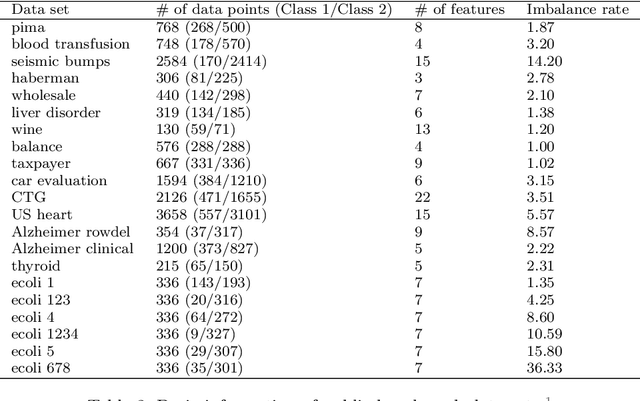
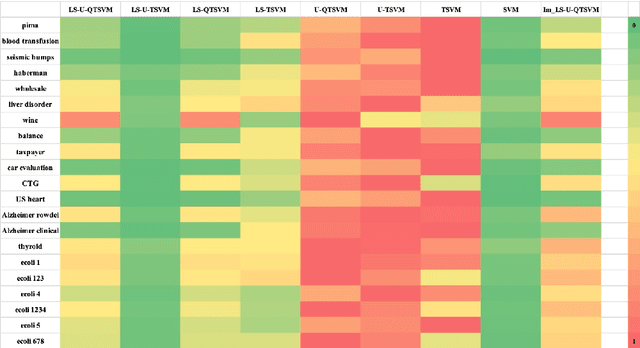
Binary classification tasks with imbalanced classes pose significant challenges in machine learning. Traditional classifiers often struggle to accurately capture the characteristics of the minority class, resulting in biased models with subpar predictive performance. In this paper, we introduce a novel approach to tackle this issue by leveraging Universum points to support the minority class within quadratic twin support vector machine models. Unlike traditional classifiers, our models utilize quadratic surfaces instead of hyperplanes for binary classification, providing greater flexibility in modeling complex decision boundaries. By incorporating Universum points, our approach enhances classification accuracy and generalization performance on imbalanced datasets. We generated four artificial datasets to demonstrate the flexibility of the proposed methods. Additionally, we validated the effectiveness of our approach through empirical evaluations on benchmark datasets, showing superior performance compared to conventional classifiers and existing methods for imbalanced classification.

A Novel Markov Model for Near-Term Railway Delay Prediction

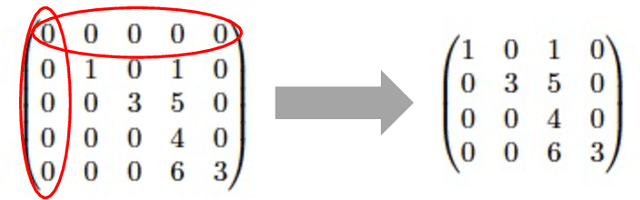
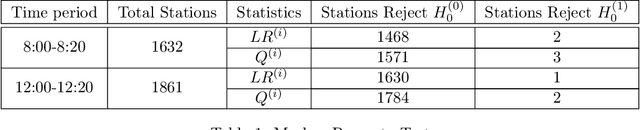
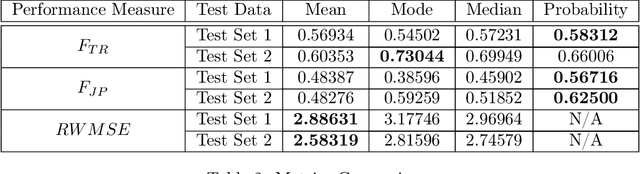
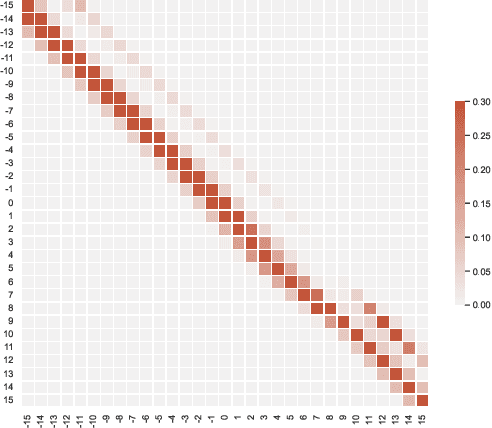
Predicting the near-future delay with accuracy for trains is momentous for railway operations and passengers' traveling experience. This work aims to design prediction models for train delays based on Netherlands Railway data. We first develop a chi-square test to show that the delay evolution over stations follows a first-order Markov chain. We then propose a delay prediction model based on non-homogeneous Markov chains. To deal with the sparsity of the transition matrices of the Markov chains, we propose a novel matrix recovery approach that relies on Gaussian kernel density estimation. Our numerical tests show that this recovery approach outperforms other heuristic approaches in prediction accuracy. The Markov chain model we propose also shows to be better than other widely-used time series models with respect to both interpretability and prediction accuracy. Moreover, our proposed model does not require a complicated training process, which is capable of handling large-scale forecasting problems.

Sparse Universum Quadratic Surface Support Vector Machine Models for Binary Classification

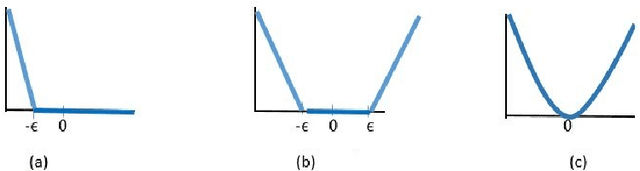
In binary classification, kernel-free linear or quadratic support vector machines are proposed to avoid dealing with difficulties such as finding appropriate kernel functions or tuning their hyper-parameters. Furthermore, Universum data points, which do not belong to any class, can be exploited to embed prior knowledge into the corresponding models so that the generalization performance is improved. In this paper, we design novel kernel-free Universum quadratic surface support vector machine models. Further, we propose the L1 norm regularized version that is beneficial for detecting potential sparsity patterns in the Hessian of the quadratic surface and reducing to the standard linear models if the data points are (almost) linearly separable. The proposed models are convex such that standard numerical solvers can be utilized for solving them. Nonetheless, we formulate a least squares version of the L1 norm regularized model and next, design an effective tailored algorithm that only requires solving one linear system. Several theoretical properties of these models are then reported/proved as well. We finally conduct numerical experiments on both artificial and public benchmark data sets to demonstrate the feasibility and effectiveness of the proposed models.

Quadratic Surface Support Vector Machine with L1 Norm Regularization

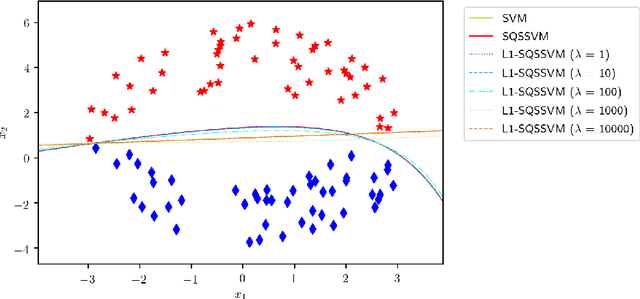
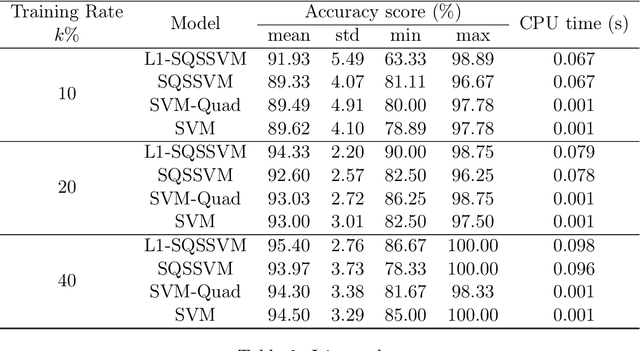
We propose $\ell_1$ norm regularized quadratic surface support vector machine models for binary classification in supervised learning. We establish their desired theoretical properties, including the existence and uniqueness of the optimal solution, reduction to the standard SVMs over (almost) linearly separable data sets, and detection of true sparsity pattern over (almost) quadratically separable data sets if the penalty parameter of $\ell_1$ norm is large enough. We also demonstrate their promising practical efficiency by conducting various numerical experiments on both synthetic and publicly available benchmark data sets.