Lanshan Han
Approaches to Linear Mixed Effects Models with Sign Constraints
Nov 09, 2020
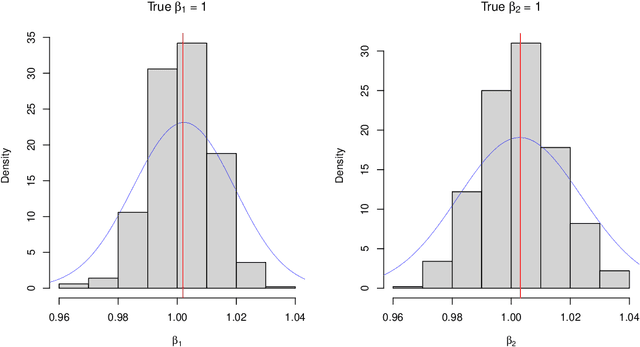
Abstract:Linear Mixed Effects (LME) models have been widely applied in clustered data analysis in many areas including marketing research, clinical trials, and biomedical studies. Inference can be conducted using maximum likelihood approach if assuming Normal distributions on the random effects. However, in many applications of economy, business and medicine, it is often essential to impose constraints on the regression parameters after taking their real-world interpretations into account. Therefore, in this paper we extend the unconstrained LME models to allow for sign constraints on its overall coefficients. We propose to assume a symmetric doubly truncated Normal (SDTN) distribution on the random effects instead of the unconstrained Normal distribution which is often found in classical literature. With the aforementioned change, difficulty has dramatically increased as the exact distribution of the dependent variable becomes analytically intractable. We then develop likelihood-based approaches to estimate the unknown model parameters utilizing the approximation of its exact distribution. Hypothesis testing under the new model specification is also discussed and studied empirically. Simulation studies have shown that the proposed constrained model not only improves real-world interpretations of results, but also achieves satisfactory performance on model fits as compared to the existing model.
Hierarchical Marketing Mix Models with Sign Constraints
Aug 28, 2020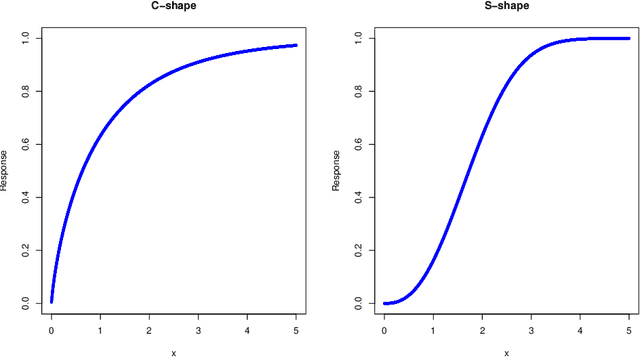

Abstract:Marketing mix models (MMMs) are statistical models for measuring the effectiveness of various marketing activities such as promotion, media advertisement, etc. In this research, we propose a comprehensive marketing mix model that captures the hierarchical structure and the carryover, shape and scale effects of certain marketing activities, as well as sign restrictions on certain coefficients that are consistent with common business sense. In contrast to commonly adopted approaches in practice, which estimate parameters in a multi-stage process, the proposed approach estimates all the unknown parameters/coefficients simultaneously using a constrained maximum likelihood approach and solved with the Hamiltonian Monte Carlo algorithm. We present results on real datasets to illustrate the use of the proposed solution algorithm.
Quadratic Surface Support Vector Machine with L1 Norm Regularization
Aug 22, 2019

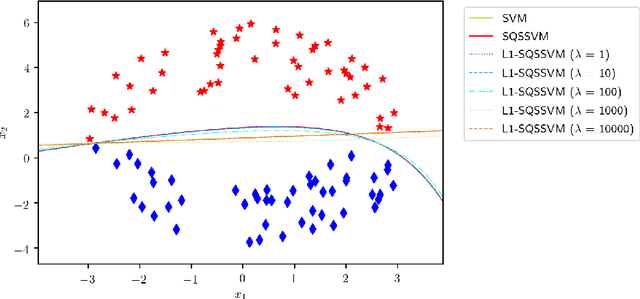
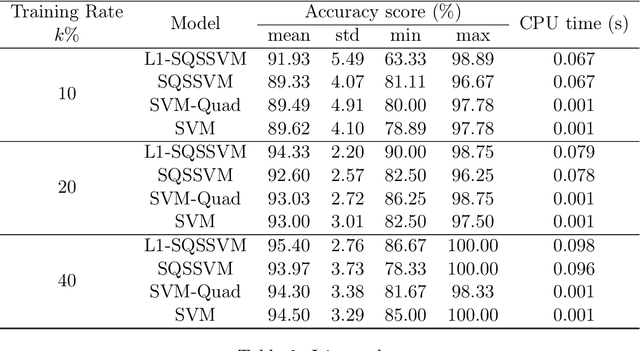
Abstract:We propose $\ell_1$ norm regularized quadratic surface support vector machine models for binary classification in supervised learning. We establish their desired theoretical properties, including the existence and uniqueness of the optimal solution, reduction to the standard SVMs over (almost) linearly separable data sets, and detection of true sparsity pattern over (almost) quadratically separable data sets if the penalty parameter of $\ell_1$ norm is large enough. We also demonstrate their promising practical efficiency by conducting various numerical experiments on both synthetic and publicly available benchmark data sets.
Beyond the EM Algorithm: Constrained Optimization Methods for Latent Class Model
Jan 09, 2019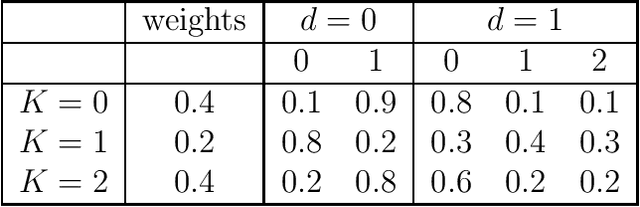
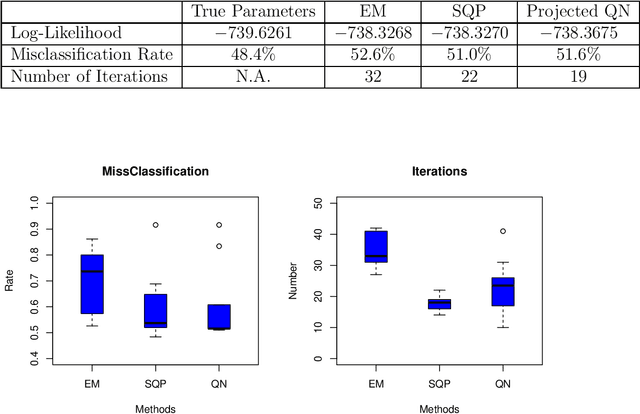
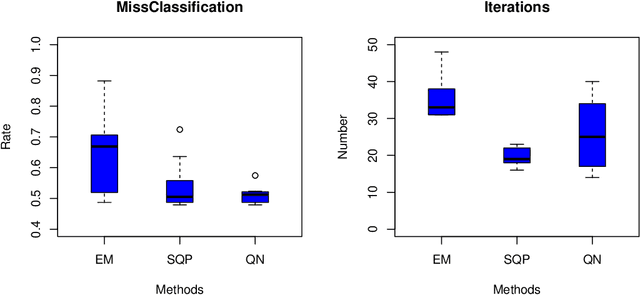

Abstract:Latent class model (LCM), which is a finite mixture of different categorical distributions, is one of the most widely used models in statistics and machine learning fields. Because of its non-continuous nature and the flexibility in shape, researchers in practice areas such as marketing and social sciences also frequently use LCM to gain insights from their data. One likelihood-based method, the Expectation-Maximization (EM) algorithm, is often used to obtain the model estimators. However, the EM algorithm is well-known for its notoriously slow convergence. In this research, we explore alternative likelihood-based methods that can potential remedy the slow convergence of the EM algorithm. More specifically, we regard likelihood-based approach as a constrained nonlinear optimization problem, and apply quasi-Newton type methods to solve them. We examine two different constrained optimization methods to maximize the log likelihood function. We present simulation study results to show that the proposed methods not only converge in less iterations than the EM algorithm but also produce more accurate model estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge