Beyond the EM Algorithm: Constrained Optimization Methods for Latent Class Model

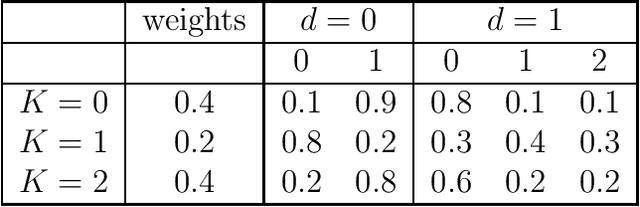
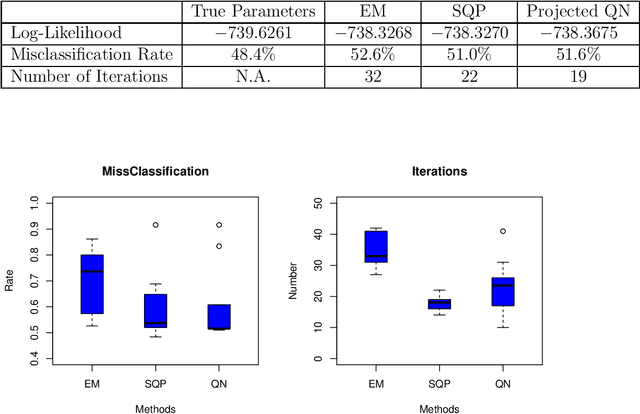
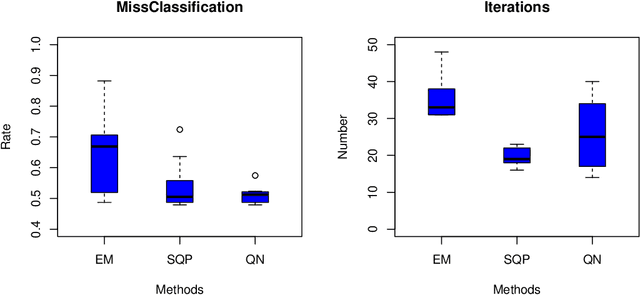
Latent class model (LCM), which is a finite mixture of different categorical distributions, is one of the most widely used models in statistics and machine learning fields. Because of its non-continuous nature and the flexibility in shape, researchers in practice areas such as marketing and social sciences also frequently use LCM to gain insights from their data. One likelihood-based method, the Expectation-Maximization (EM) algorithm, is often used to obtain the model estimators. However, the EM algorithm is well-known for its notoriously slow convergence. In this research, we explore alternative likelihood-based methods that can potential remedy the slow convergence of the EM algorithm. More specifically, we regard likelihood-based approach as a constrained nonlinear optimization problem, and apply quasi-Newton type methods to solve them. We examine two different constrained optimization methods to maximize the log likelihood function. We present simulation study results to show that the proposed methods not only converge in less iterations than the EM algorithm but also produce more accurate model estimators.