A Penalty Based Method for Communication-Efficient Decentralized Bilevel Programming

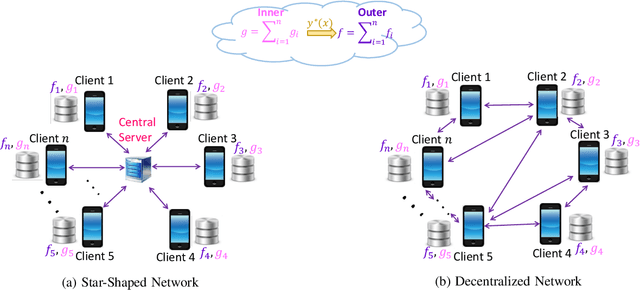
Bilevel programming has recently received attention in the literature, due to a wide range of applications, including reinforcement learning and hyper-parameter optimization. However, it is widely assumed that the underlying bilevel optimization problem is solved either by a single machine or in the case of multiple machines connected in a star-shaped network, i.e., federated learning setting. The latter approach suffers from a high communication cost on the central node (e.g., parameter server) and exhibits privacy vulnerabilities. Hence, it is of interest to develop methods that solve bilevel optimization problems in a communication-efficient decentralized manner. To that end, this paper introduces a penalty function based decentralized algorithm with theoretical guarantees for this class of optimization problems. Specifically, a distributed alternating gradient-type algorithm for solving consensus bilevel programming over a decentralized network is developed. A key feature of the proposed algorithm is to estimate the hyper-gradient of the penalty function via decentralized computation of matrix-vector products and few vector communications, which is then integrated within our alternating algorithm to give the finite-time convergence analysis under different convexity assumptions. Owing to the generality of this complexity analysis, our result yields convergence rates for a wide variety of consensus problems including minimax and compositional optimization. Empirical results on both synthetic and real datasets demonstrate that the proposed method works well in practice.

Dynamic Regret of Adaptive Gradient Methods for Strongly Convex Problems

Adaptive gradient algorithms such as ADAGRAD and its variants have gained popularity in the training of deep neural networks. While many works as for adaptive methods have focused on the static regret as a performance metric to achieve a good regret guarantee, the dynamic regret analyses of these methods remain unclear. As opposed to the static regret, dynamic regret is considered to be a stronger concept of performance measurement in the sense that it explicitly elucidates the non-stationarity of the environment. In this paper, we go through a variant of ADAGRAD (referred to as M-ADAGRAD ) in a strong convex setting via the notion of dynamic regret, which measures the performance of an online learner against a reference (optimal) solution that may change over time. We demonstrate a regret bound in terms of the path-length of the minimizer sequence that essentially reflects the non-stationarity of environments. In addition, we enhance the dynamic regret bound by exploiting the multiple accesses of the gradient to the learner in each round. Empirical results indicate that M-ADAGRAD works also well in practice.

Dynamic Regret Analysis for Online Meta-Learning

The online meta-learning framework has arisen as a powerful tool for the continual lifelong learning setting. The goal for an agent is to quickly learn new tasks by drawing on prior experience, while it faces with tasks one after another. This formulation involves two levels: outer level which learns meta-learners and inner level which learns task-specific models, with only a small amount of data from the current task. While existing methods provide static regret analysis for the online meta-learning framework, we establish performance in terms of dynamic regret which handles changing environments from a global prospective. We also build off of a generalized version of the adaptive gradient methods that covers both ADAM and ADAGRAD to learn meta-learners in the outer level. We carry out our analyses in a stochastic setting, and in expectation prove a logarithmic local dynamic regret which depends explicitly on the total number of iterations T and parameters of the learner. Apart from, we also indicate high probability bounds on the convergence rates of proposed algorithm with appropriate selection of parameters, which have not been argued before.

Adaptive First-and Zeroth-order Methods for Weakly Convex Stochastic Optimization Problems

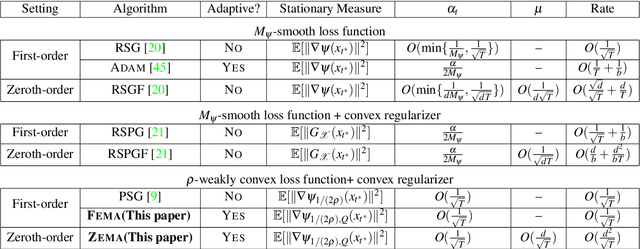
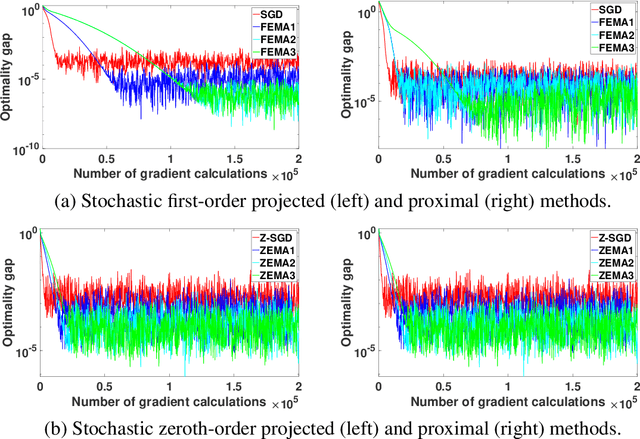
In this paper, we design and analyze a new family of adaptive subgradient methods for solving an important class of weakly convex (possibly nonsmooth) stochastic optimization problems. Adaptive methods that use exponential moving averages of past gradients to update search directions and learning rates have recently attracted a lot of attention for solving optimization problems that arise in machine learning. Nevertheless, their convergence analysis almost exclusively requires smoothness and/or convexity of the objective function. In contrast, we establish non-asymptotic rates of convergence of first and zeroth-order adaptive methods and their proximal variants for a reasonably broad class of nonsmooth \& nonconvex optimization problems. Experimental results indicate how the proposed algorithms empirically outperform stochastic gradient descent and its zeroth-order variant for solving such optimization problems.

DADAM: A Consensus-based Distributed Adaptive Gradient Method for Online Optimization

Adaptive gradient-based optimization methods such as ADAGRAD, RMSPROP, and ADAM are widely used in solving large-scale machine learning problems including deep learning. A number of schemes have been proposed in the literature aiming at parallelizing them, based on communications of peripheral nodes with a central node, but incur high communications cost. To address this issue, we develop a novel consensus-based distributed adaptive moment estimation method (DADAM) for online optimization over a decentralized network that enables data parallelization, as well as decentralized computation. The method is particularly useful, since it can accommodate settings where access to local data is allowed. Further, as established theoretically in this work, it can outperform centralized adaptive algorithms, for certain classes of loss functions used in applications. We analyze the convergence properties of the proposed algorithm and provide a dynamic regret bound on the convergence rate of adaptive moment estimation methods in both stochastic and deterministic settings. Empirical results demonstrate that DADAM works also well in practice and compares favorably to competing online optimization methods.