Adaptive First-and Zeroth-order Methods for Weakly Convex Stochastic Optimization Problems
Paper and Code
May 24, 2020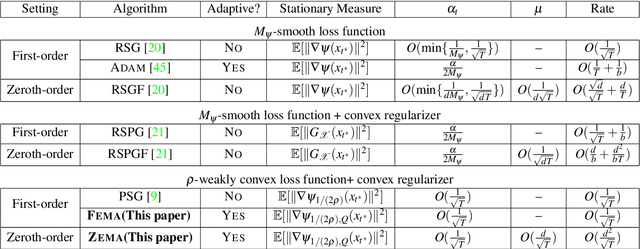
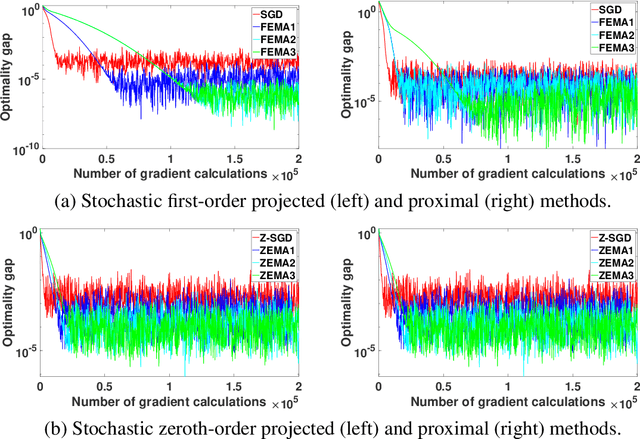

In this paper, we design and analyze a new family of adaptive subgradient methods for solving an important class of weakly convex (possibly nonsmooth) stochastic optimization problems. Adaptive methods that use exponential moving averages of past gradients to update search directions and learning rates have recently attracted a lot of attention for solving optimization problems that arise in machine learning. Nevertheless, their convergence analysis almost exclusively requires smoothness and/or convexity of the objective function. In contrast, we establish non-asymptotic rates of convergence of first and zeroth-order adaptive methods and their proximal variants for a reasonably broad class of nonsmooth \& nonconvex optimization problems. Experimental results indicate how the proposed algorithms empirically outperform stochastic gradient descent and its zeroth-order variant for solving such optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge