An Algebraic Geometry Approach to Viewing Graph Solvability

The concept of viewing graph solvability has gained significant interest in the context of structure-from-motion. A viewing graph is a mathematical structure where nodes are associated to cameras and edges represent the epipolar geometry connecting overlapping views. Solvability studies under which conditions the cameras are uniquely determined by the graph. In this paper we propose a novel framework for analyzing solvability problems based on Algebraic Geometry, demonstrating its potential in understanding structure-from-motion graphs and proving a conjecture that was previously proposed.

Minimal Perspective Autocalibration

We introduce a new family of minimal problems for reconstruction from multiple views. Our primary focus is a novel approach to autocalibration, a long-standing problem in computer vision. Traditional approaches to this problem, such as those based on Kruppa's equations or the modulus constraint, rely explicitly on the knowledge of multiple fundamental matrices or a projective reconstruction. In contrast, we consider a novel formulation involving constraints on image points, the unknown depths of 3D points, and a partially specified calibration matrix $K$. For $2$ and $3$ views, we present a comprehensive taxonomy of minimal autocalibration problems obtained by relaxing some of these constraints. These problems are organized into classes according to the number of views and any assumed prior knowledge of $K$. Within each class, we determine problems with the fewest -- or a relatively small number of -- solutions. From this zoo of problems, we devise three practical solvers. Experiments with synthetic and real data and interfacing our solvers with COLMAP demonstrate that we achieve superior accuracy compared to state-of-the-art calibration methods. The code is available at https://github.com/andreadalcin/MinimalPerspectiveAutocalibration

MinBackProp -- Backpropagating through Minimal Solvers

We present an approach to backpropagating through minimal problem solvers in end-to-end neural network training. Traditional methods relying on manually constructed formulas, finite differences, and autograd are laborious, approximate, and unstable for complex minimal problem solvers. We show that using the Implicit function theorem to calculate derivatives to backpropagate through the solution of a minimal problem solver is simple, fast, and stable. We compare our approach to (i) using the standard autograd on minimal problem solvers and relate it to existing backpropagation formulas through SVD-based and Eig-based solvers and (ii) implementing the backprop with an existing PyTorch Deep Declarative Networks (DDN) framework. We demonstrate our technique on a toy example of training outlier-rejection weights for 3D point registration and on a real application of training an outlier-rejection and RANSAC sampling network in image matching. Our method provides $100\%$ stability and is 10 times faster compared to autograd, which is unstable and slow, and compared to DDN, which is stable but also slow.

Socially Pertinent Robots in Gerontological Healthcare

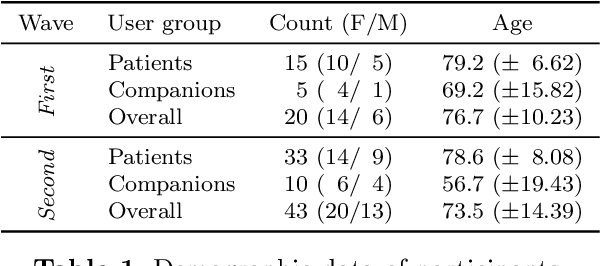
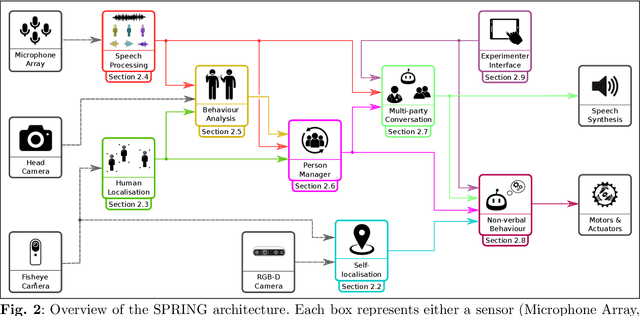
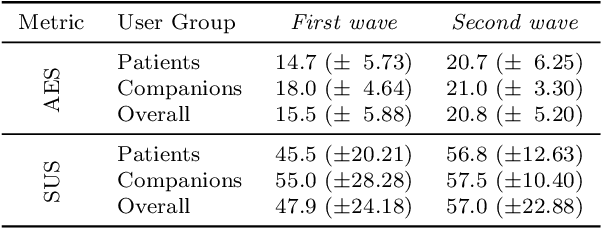
Despite the many recent achievements in developing and deploying social robotics, there are still many underexplored environments and applications for which systematic evaluation of such systems by end-users is necessary. While several robotic platforms have been used in gerontological healthcare, the question of whether or not a social interactive robot with multi-modal conversational capabilities will be useful and accepted in real-life facilities is yet to be answered. This paper is an attempt to partially answer this question, via two waves of experiments with patients and companions in a day-care gerontological facility in Paris with a full-sized humanoid robot endowed with social and conversational interaction capabilities. The software architecture, developed during the H2020 SPRING project, together with the experimental protocol, allowed us to evaluate the acceptability (AES) and usability (SUS) with more than 60 end-users. Overall, the users are receptive to this technology, especially when the robot perception and action skills are robust to environmental clutter and flexible to handle a plethora of different interactions.

Order-One Rolling Shutter Cameras

Rolling shutter (RS) cameras dominate consumer and smartphone markets. Several methods for computing the absolute pose of RS cameras have appeared in the last 20 years, but the relative pose problem has not been fully solved yet. We provide a unified theory for the important class of order-one rolling shutter (RS$_1$) cameras. These cameras generalize the perspective projection to RS cameras, projecting a generic space point to exactly one image point via a rational map. We introduce a new back-projection RS camera model, characterize RS$_1$ cameras, construct explicit parameterizations of such cameras, and determine the image of a space line. We classify all minimal problems for solving the relative camera pose problem with linear RS$_1$ cameras and discover new practical cases. Finally, we show how the theory can be used to explain RS models previously used for absolute pose computation.

Automatic Solver Generator for Systems of Laurent Polynomial Equations

In computer vision applications, the following problem often arises: Given a family of (Laurent) polynomial systems with the same monomial structure but varying coefficients, find a solver that computes solutions for any family member as fast as possible. Under appropriate genericity assumptions, the dimension and degree of the respective polynomial ideal remain unchanged for each particular system in the same family. The state-of-the-art approach to solving such problems is based on elimination templates, which are the coefficient (Macaulay) matrices that encode the transformation from the initial polynomials to the polynomials needed to construct the action matrix. Knowing an action matrix, the solutions of the system are computed from its eigenvectors. The important property of an elimination template is that it applies to all polynomial systems in the family. In this paper, we propose a new practical algorithm that checks whether a given set of Laurent polynomials is sufficient to construct an elimination template. Based on this algorithm, we propose an automatic solver generator for systems of Laurent polynomial equations. The new generator is simple and fast; it applies to ideals with positive-dimensional components; it allows one to uncover partial $p$-fold symmetries automatically. We test our generator on various minimal problems, mostly in geometric computer vision. The speed of the generated solvers exceeds the state-of-the-art in most cases. In particular, we propose the solvers for the following problems: optimal 3-view triangulation, semi-generalized hybrid pose estimation and minimal time-of-arrival self-calibration. The experiments on synthetic scenes show that our solvers are numerically accurate and either comparable to or significantly faster than the state-of-the-art solvers.

D-InLoc++: Indoor Localization in Dynamic Environments

Most state-of-the-art localization algorithms rely on robust relative pose estimation and geometry verification to obtain moving object agnostic camera poses in complex indoor environments. However, this approach is prone to mistakes if a scene contains repetitive structures, e.g., desks, tables, boxes, or moving people. We show that the movable objects incorporate non-negligible localization error and present a new straightforward method to predict the six-degree-of-freedom (6DoF) pose more robustly. We equipped the localization pipeline InLoc with real-time instance segmentation network YOLACT++. The masks of dynamic objects are employed in the relative pose estimation step and in the final sorting of camera pose proposal. At first, we filter out the matches laying on masks of the dynamic objects. Second, we skip the comparison of query and synthetic images on the area related to the moving object. This procedure leads to a more robust localization. Lastly, we describe and improve the mistakes caused by gradient-based comparison between synthetic and query images and publish a new pipeline for simulation of environments with movable objects from the Matterport scans. All the codes are available on github.com/dubenma/D-InLocpp .

Objects Can Move: 3D Change Detection by Geometric Transformation Constistency

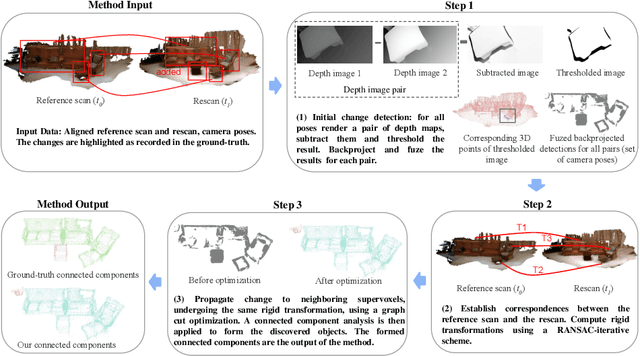
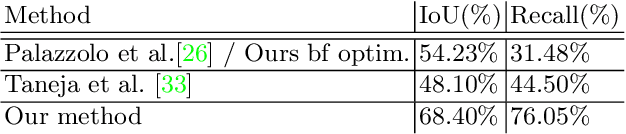
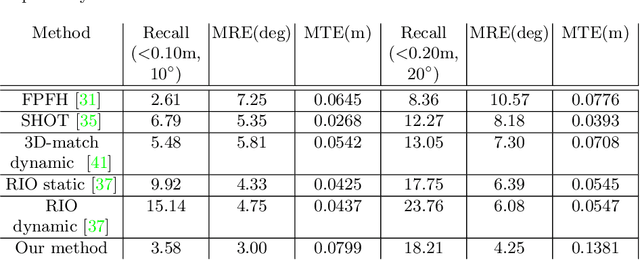
AR/VR applications and robots need to know when the scene has changed. An example is when objects are moved, added, or removed from the scene. We propose a 3D object discovery method that is based only on scene changes. Our method does not need to encode any assumptions about what is an object, but rather discovers objects by exploiting their coherent move. Changes are initially detected as differences in the depth maps and segmented as objects if they undergo rigid motions. A graph cut optimization propagates the changing labels to geometrically consistent regions. Experiments show that our method achieves state-of-the-art performance on the 3RScan dataset against competitive baselines. The source code of our method can be found at https://github.com/katadam/ObjectsCanMove.

Optimizing Elimination Templates by Greedy Parameter Search

We propose a new method for constructing elimination templates for efficient polynomial system solving of minimal problems in structure from motion, image matching, and camera tracking. We first construct a particular affine parameterization of the elimination templates for systems with a finite number of distinct solutions. Then, we use a heuristic greedy optimization strategy over the space of parameters to get a template with a small size. We test our method on 34 minimal problems in computer vision. For all of them, we found the templates either of the same or smaller size compared to the state-of-the-art. For some difficult examples, our templates are, e.g., 2.1, 2.5, 3.8, 6.6 times smaller. For the problem of refractive absolute pose estimation with unknown focal length, we have found a template that is 20 times smaller. Our experiments on synthetic data also show that the new solvers are fast and numerically accurate. We also present a fast and numerically accurate solver for the problem of relative pose estimation with unknown common focal length and radial distortion.

Learning to Solve Hard Minimal Problems

We present an approach to solving hard geometric optimization problems in the RANSAC framework. The hard minimal problems arise from relaxing the original geometric optimization problem into a minimal problem with many spurious solutions. Our approach avoids computing large numbers of spurious solutions. We design a learning strategy for selecting a starting problem-solution pair that can be numerically continued to the problem and the solution of interest. We demonstrate our approach by developing a RANSAC solver for the problem of computing the relative pose of three calibrated cameras, via a minimal relaxation using four points in each view. On average, we can solve a single problem in under 70 $\mu s.$ We also benchmark and study our engineering choices on the very familiar problem of computing the relative pose of two calibrated cameras, via the minimal case of five points in two views.